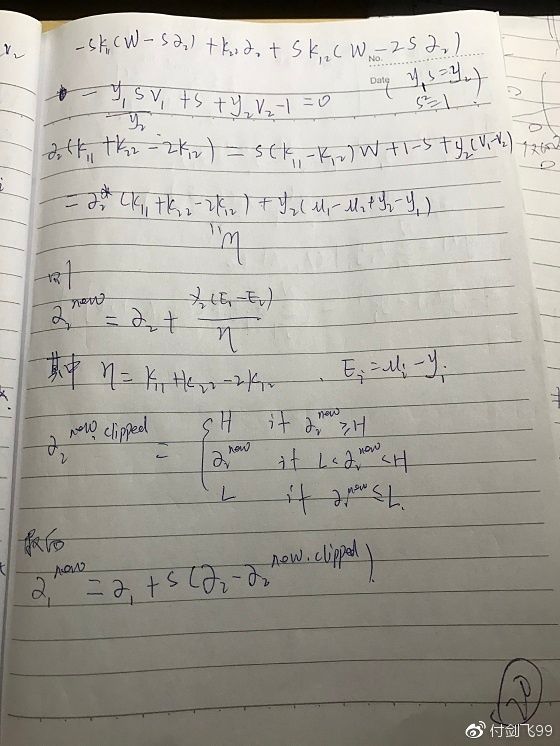连续推导了两天的公式外加一天的编程,身体和脑子已不是自己的了。今天傍晚还没实现,到了快晚饭时间才调试通过得到了不错的结果,下午是崩溃的,一直收敛不了,找了许久也没找到什么原因导致的,于是开始怀疑人生。没办法,只好一步一步调试过去,终于被我找到某个地方的j写成了i,还有之前的大于号写成了小于号…这么多复杂的公式,有一处小的地方写错了,原因真的很难找到。要不是因为它好玩,我才不想干这种苦逼的事呢。
又出Bug了,登不进去,只好用微薄
话不多说,上公式:
上程序:
'''
Created on 2017年7月9日
@author: fujianfei
'''
from os.path import os
import numpy as np
#导入数据,数据集
def loadDataSet (fileName):
data_path = os.getcwd()+'\\data\\'
labelMat = []
svmData = np.loadtxt(data_path+fileName,delimiter=',')
dataMat=svmData[:,0:2]
#零均值化
# meanVal=np.mean(dataMat,axis=0)
# dataMat=dataMat-meanVal
label=svmData[:,2]
for i in range (np.size(label)):
if label[i] == 0 or label[i] == -1:
labelMat.append(float(-1))
if label[i] == 1:
labelMat.append(float(1))
return dataMat.tolist(),labelMat
#简化版SMO算法,不启用启发式选择alpha,先随机选
def selectJrand(i,m):
j=i
while (j==i):
j = int(np.random.uniform(0,m))#在0-m的随机选一个数
return j
#用于调整大于H或小于L的值,剪辑最优解
def clipAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
'''
定义核函数
kernelOption=linear 线性
kernelOption=rbf 高斯核函数
'''
def calcKernelValue(matrix_x, sample_x, kernelOption):
kernelType = kernelOption[0]
numSamples = matrix_x.shape[0]
kernelValue = np.mat(np.zeros((numSamples, 1)))
if kernelType == 'linear':
kernelValue = matrix_x.dot(sample_x.T)
elif kernelType == 'rbf':
sigma = kernelOption[1]
if sigma == 0:
sigma = 1.0
for i in range(numSamples):
diff = matrix_x[i, :] - sample_x
kernelValue[i] = np.exp(diff.dot(diff.T) / (-2.0 * sigma**2))
else:
raise NameError('Not support kernel type! You can use linear or rbf!')
return kernelValue
'''
简化版SMO算法。
dataMatIn:输入的数据集
classLabels:类别标签
C:松弛变量前的常数
toler:容错率
maxIter:最大循环数
'''
def smoSimple(dataMatIn,classLabels,C,toler,maxIter):
dataMatrix = np.mat(dataMatIn);labelMat = np.mat(classLabels).transpose()
b=0;m,n = np.shape(dataMatrix)
alphas = np.mat(np.zeros((m,1)))
iter = 0
while(iter < maxIter):
alphaPairsChanged = 0 #记录alpha值是否优化,即是否变化
for i in range(m):#遍历数据集,第一层循环,遍历所有的alpha
fXi = float(np.multiply(alphas,labelMat).T.dot(calcKernelValue(dataMatrix,dataMatrix[i,:],('linear', 0)))) + b
Ei = fXi - float(labelMat[i])
if (((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0))):
j = selectJrand(i, m)
fXj = float(np.multiply(alphas,labelMat).T.dot(calcKernelValue(dataMatrix,dataMatrix[j,:],('linear', 0)))) + b
Ej = fXj - float(labelMat[j])
alphaIold = alphas[i].copy();
alphaJold = alphas[j].copy();
if (labelMat[i] != labelMat[j]):
L = max(0,alphas[j] - alphas[i])
H = min(C,C+alphas[j] - alphas[i])
else:
L = max(0,alphas[j] + alphas[i] -C)
H = min(C,alphas[j] + alphas[i])
if(L == H):print('L==H');continue
eta = 2.0 * calcKernelValue(dataMatrix[i,:],dataMatrix[j,:],('linear', 0)) - calcKernelValue(dataMatrix[i,:],dataMatrix[i,:],('linear', 0)) - calcKernelValue(dataMatrix[j,:],dataMatrix[j,:],('linear', 0))
if(eta >= 0):print('eta >= 0');continue
alphas[j] -= labelMat[j] * (Ei - Ej)/eta
alphas[j] = clipAlpha(alphas[j], H, L)
if (abs(alphas[j]-alphaJold) < 0.0001) : print('j not moving enough');continue
alphas[i] += labelMat[i]*labelMat[j]*(alphaJold - alphas[j])
b1 = b - Ei - labelMat[i]*(alphas[i] - alphaIold)*calcKernelValue(dataMatrix[i,:],dataMatrix[i,:],('linear', 0)) - labelMat[j]*(alphas[j]-alphaJold)*calcKernelValue(dataMatrix[j,:],dataMatrix[i,:],('linear', 0))
b2 = b - Ej - labelMat[i]*(alphas[i] - alphaIold)*calcKernelValue(dataMatrix[i,:],dataMatrix[j,:],('linear', 0)) - labelMat[j]*(alphas[j]-alphaJold)*calcKernelValue(dataMatrix[j,:],dataMatrix[j,:],('linear', 0))
if (0 < alphas[i] and (C > alphas[i])):b=b1
elif (0 < alphas[j] and (C > alphas[j])):b=b2
else:b=(b1+b2)/2.0
alphaPairsChanged += 1
print("iter:%d i:%d,pairs changed %d" % (iter,i,alphaPairsChanged))
if(alphaPairsChanged == 0) :
iter += 1
else :
iter = 0
print("iteration number:%d" % iter)
return b,alphas
from SVM import svmMLiA
import numpy as np
import matplotlib.pyplot as plt
#实现,并可视化
if __name__ == '__main__':
dataMatIn,classLabels = svmMLiA.loadDataSet('data1.txt')
dataMatrix = np.mat(dataMatIn);labelMat = np.mat(classLabels).transpose()
C=0.6
toler=0.001
maxIter=40
m,n = np.shape(dataMatrix)
b,alphas = svmMLiA.smoSimple(dataMatIn, classLabels, C, toler, maxIter)
w=np.multiply(alphas,labelMat).T.dot(dataMatrix)
w=np.mat(w)
x1=dataMatrix[:,0]
y1=dataMatrix[:,1]
x2=range(20,100)
b=float(b)
w0=float(w[0,0])
w1=float(w[0,1])
y2 = [-b/w1-w0/w1*elem for elem in x2]
plt.plot(x2, y2)
for i in range(m):
if ((alphas[i] < C) and (alphas[i] > 0)):
print('########################')
print(alphas[i])
plt.scatter(x1[i], y1[i],s=60,c='red',marker='o',alpha=0.5,label='SV')
if int(labelMat[i, 0]) == -1:
plt.scatter(x1[i], y1[i],s=30,c='red',marker='.',alpha=0.5,label='-1')
elif int(labelMat[i, 0]) == 1:
plt.scatter(x1[i], y1[i],s=30,c='blue',marker='x',alpha=0.5,label='+1')
plt.show()
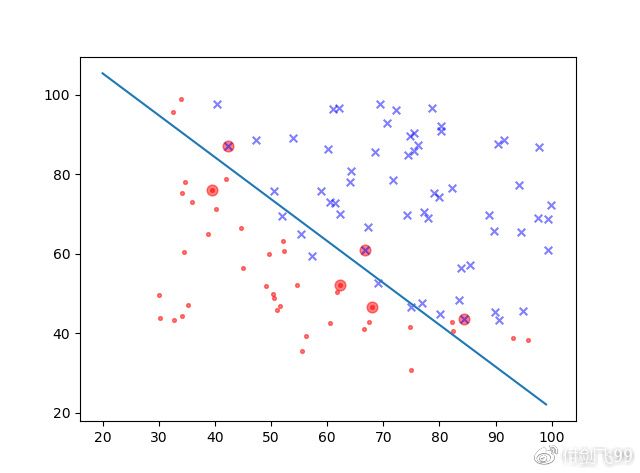
最后的结果是这样滴:
说明:大大的红色的圈圈就是支持向量。
支持向量机的功能绝不限于此,这个东西早在数周前用逻辑斯特回归早就画出来了。关于支持向量的其他更高级应用下周再说。包括高斯核和启发式选择初始值,这次的是简单版本的SMO算法,因为随便选的,速度慢的要死。几百个数据点就跑了好几分钟。