正文之前
在之前的【离散数学】图论中谈到过图的同构,今天我们来谈谈树的同构:
同构树
同构有根树
同构二叉树
正文
同构树
1. 简介
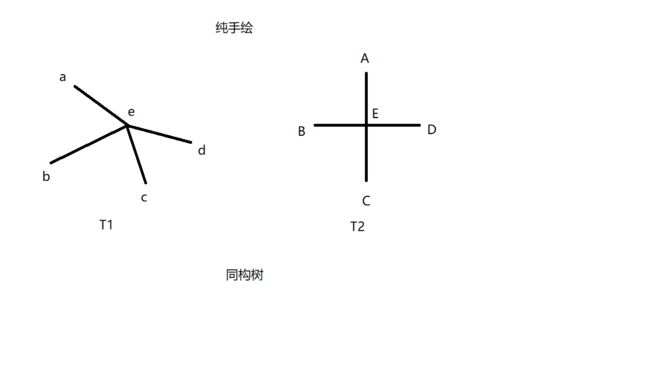
T1和T2为同构树,当且仅当存在一个从T1的结点到T2的结点的一对一的映上函数 f (one - to - one and onto function f )
简而言之,如果T1和T2为同构树,在T1中结点 v 和 w 相邻,则在T2中的结点 f (v) 和 f(w) 也相邻
上图中:
- a - A
- b - B
- c - C
- d - D
- e - E
2. 判断
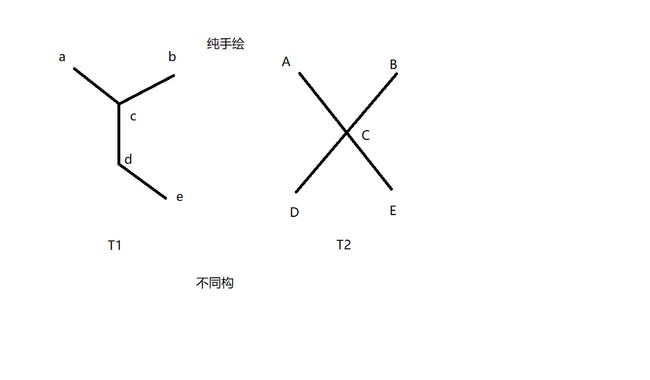
如果T1中某些特性没有表明在T2中,就能够表明两棵树不同构
T1中有度数为2,3的结点,而T2中没有,所以T1和T2不同构
同构有根树
1. 简介
同构有根树的条件是基于同构树之上的:
T1的结点到T2的结点的一对一的映上函数 f (one - to - one and onto function f )
还必须保持根结点的一致性
也就是说,如果T1的根结点为 v ,则T2的根结点为 f(v)
若 v1 为T1的根结点, v2 为T2的根结点,所以T1和T2同构需满足
- T1中结点 v 和 w 相邻,则T2中的结点 f (v) 和 f(w) 也相邻
- f(v1) = v2
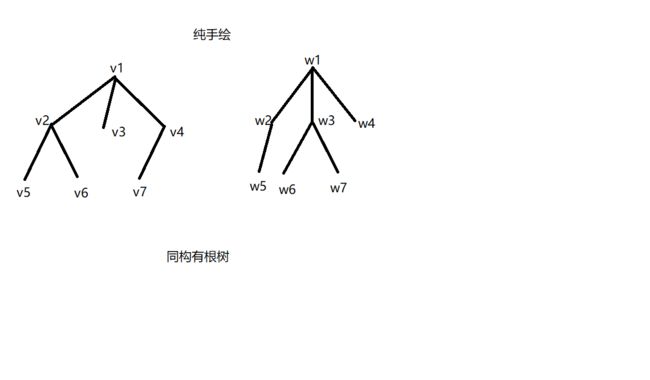
上图中:(注意下标)
- v1 - w1
- v2 - w3
- v3 - w4
- v4 - w2
- v5 - w6
- v6 - w7
- v7 - w5
2. 判断
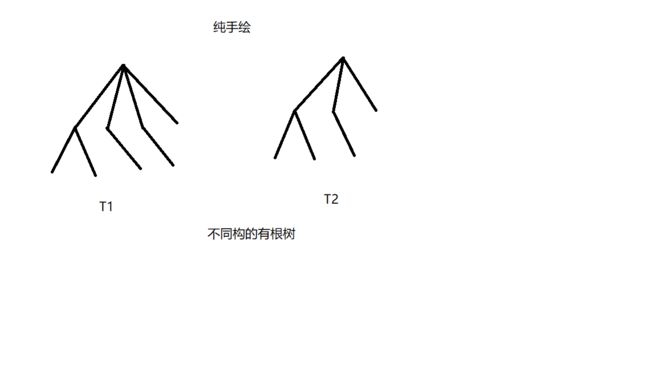
同构有根树的判断和同构树的判断相同,只需要找一些不同的特性
上图中,T1的根结点的度为4,而T2的根结点的度为3,所以两树不同构
同构二叉树
1. 简介
同构二叉树的条件是基于同构有根树之上的:
不仅需要保持结点的相邻关系和根的一致性,还需要保持左右子节点的一致性
若T1是根结点为 v1 的二叉树,T2是根结点为 v2 的二叉树,所以T1和T2同构需满足:
- T1中结点 v 和 w 相邻,则T2中的结点 f (v) 和 f(w) 也相邻
- f(v1) = v2
- vi 是T1中结点 v 的左子节点,则 f(vi) 是T1中结点 f(v) 的左子节点
- vj 是T1中结点 v 的右子节点,则 f(vj) 是T1中结点 f(v) 的右子节点
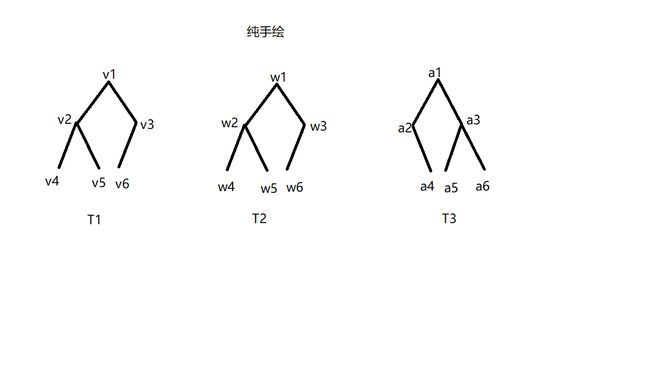
上图中,T1和T2同构,T1和T3不同构:
- v1 - w1
- v2 - w2
- v3 - w3
- v4 - w4
- v5 - w5
- v6 - w6
2. 判断
同构二叉树的判断如同上述,只需要找一些不同的特性
以上图来说,T1中,v3没有右子节点,而在T3中,a3却有右子节点,所以两树不同构
划重点
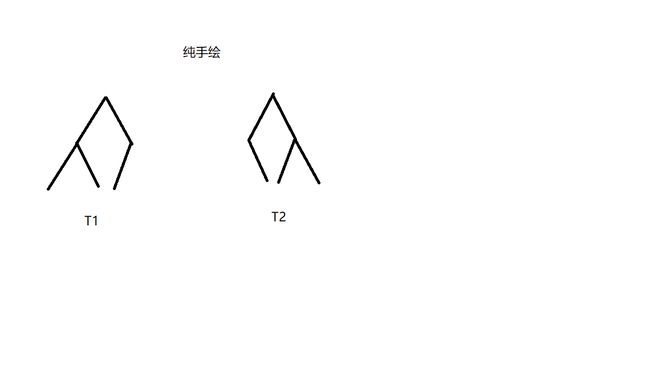
对于两棵树是否同构,需要分情况来判断:
对于上图中两棵树,作为二叉树,两棵树不同构,但是,作为有根树或自由树,这两棵树是同构的
关于树的同构就介绍到此了,谢谢!