大家好!我是一名执着的Android开发攻城狮,第一次写,没有写好的希望大家多多包涵,万事开头难,从去年开始我就想写点自己的东西,但是一直没有写下去的勇气和毅力,希望这是我一个好的习惯开始。在这我先模仿一个,贝塞尔曲线的基本原理,在这里我就不说了,不论还是其他论坛上都有很多介绍,在这里我推荐:Android -- 贝塞尔曲线公式的推导和简单使用,写的还是很不错的,当然也有其他大神写的,在这就不一一列举了,百度一下,一大篇。
先说下我我编写的步骤和思路,完整的代码在最后面:
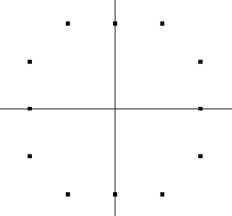
1、我需要哪些来辅助我实现“圆渐变心”,第一个就是我需要一个坐标系(mCentreX,mCentreY)
canvas.drawLine(0,mCentreY,viewWidth,mCentreY,mCoordinatePaint);
canvas.drawLine(mCentreX,0,mCentreX,viewHigh,mCoordinatePaint);
2、我需要贝塞尔三阶曲线来画圆,实际上就和贝塞尔二阶曲线两个数据控制点一样,我将圆划分为四块
每块一个贝塞尔三阶曲线圆弧。所以需要4个数据点,八个控制点
//添加数据点
mPointDatas.add(newPointF(mCentreX,mCentreY-mControlRadius));
mPointDatas.add(newPointF(mCentreX+mControlRadius,mCentreY));
mPointDatas.add(newPointF(mCentreX,mCentreY+mControlRadius));
mPointDatas.add(newPointF(mCentreX-mControlRadius,mCentreY));
//添加控制点
mPointControlls.add(newPointF(mCentreX+mControlRadius*stu,mCentreY-mControlRadius));
mPointControlls.add(newPointF(mCentreX+mControlRadius,mCentreY-mControlRadius*stu));
mPointControlls.add(newPointF(mCentreX+mControlRadius,mCentreY+mControlRadius*stu));
mPointControlls.add(newPointF(mCentreX+mControlRadius*stu,mCentreY+mControlRadius));
mPointControlls.add(newPointF(mCentreX-mControlRadius*stu,mCentreY+mControlRadius));
mPointControlls.add(newPointF(mCentreX-mControlRadius,mCentreY+mControlRadius*stu));
mPointControlls.add(newPointF(mCentreX-mControlRadius,mCentreY-mControlRadius*stu));
mPointControlls.add(newPointF(mCentreX-mControlRadius*stu,mCentreY-mControlRadius));
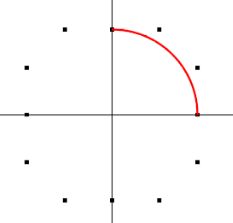
坐标系上的四个点位为数据点,其他点为控制点。然后一个贝塞尔三阶曲线画出四分之一圆弧
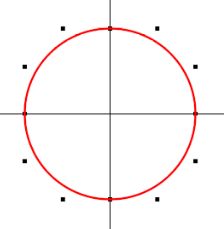
然后循环画出圆
//贝塞尔三阶曲线
for(inti =0; i
if(i < (mPointDatas.size() -1)) {
Pathpath =newPath();
path.moveTo(mPointDatas.get(i).x,mPointDatas.get(i).y);
path.cubicTo(mPointControlls.get(i*2).x,mPointControlls.get(i*2).y,mPointControlls.get(i*2+1).x,mPointControlls.get(i*2+1).y,
mPointDatas.get(i+1).x,mPointDatas.get(i+1).y);
//绘制路径
canvas.drawPath(path,mPaintBezier);
}else{
Pathpath =newPath();
path.moveTo(mPointDatas.get(i).x,mPointDatas.get(i).y);
path.cubicTo(mPointControlls.get(i*2).x,mPointControlls.get(i*2).y,mPointControlls.get(i*2+1).x,mPointControlls.get(i*2+1).y,
mPointDatas.get(0).x,mPointDatas.get(0).y);
//绘制路径
canvas.drawPath(path,mPaintBezier);
}
}
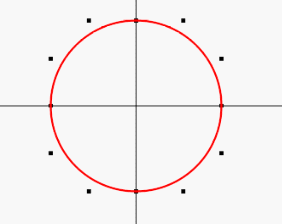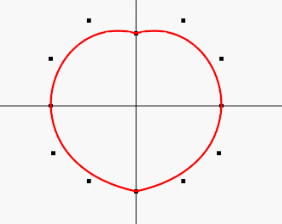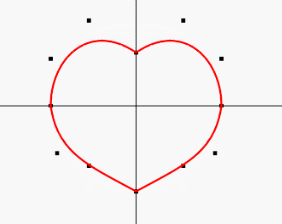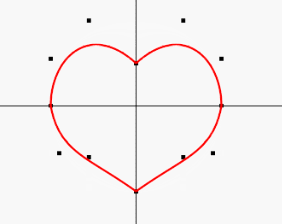
3、最后一块就是圆边成心操作,数据点我们需要操作最顶端的一个数据点就好,控制点也只需要操作下面四个数据点即可
if(count*rate<100) {
mPointDatas.get(0).y=mPointDatas.get(0).y+1f*rate;
mPointControlls.get(2).x=mPointControlls.get(2).x-0.2f*rate;
mPointControlls.get(3).y=mPointControlls.get(3).y-0.8f*rate;
mPointControlls.get(4).y=mPointControlls.get(4).y-0.8f*rate;
mPointControlls.get(5).x=mPointControlls.get(5).x+0.2f*rate;
invalidate();
count++;
handler.postDelayed(this,50);
}
设置一个定时器执行上面重复执行上面操作就可以实现圆边心
以上就实现了贝塞尔曲线——圆渐变心,下面是全部主要代码(代码里有扩展实现变四叶草、变水滴):
//画布大小
private intviewWidth,viewHigh;
//画布中心点坐标
private intmCentreX,mCentreY;
//坐标画笔
privatePaintmCoordinatePaint;
//控制点、数据点画笔
privatePaintmPaintPoint;
//画圆画笔
privatePaintmPaintBezier;
//数据点半径
private intmControlRadius=200;
//放置四个数据点的集合
privateListmPointDatas;
//方式8个控制点的集合
privateListmPointControlls;
//常量0.552284749831
private floatstu=0.552284749831f;
//圆变心进行变化计数
private intcount=0;
//变化类型
private intchangeType=0;
//变化速率
private floatrate=5f;
publicBezierCurveThreeView(Contextcontext) {
super(context);
}
publicBezierCurveThreeView(Contextcontext,AttributeSetattrs) {
super(context,attrs);
initPaint();
}
publicBezierCurveThreeView(Contextcontext,AttributeSetattrs,intdefStyleAttr) {
super(context,attrs,defStyleAttr);
}
private voidinitPaint(){
count=0;
//初始化坐标画笔
mCoordinatePaint=newPaint();
mCoordinatePaint.setStyle(Paint.Style.STROKE);
mCoordinatePaint.setColor(Color.BLACK);
mCoordinatePaint.setStrokeWidth(2);
//初始化控制点、数据点画笔
mPaintPoint=newPaint();
mPaintPoint.setColor(Color.BLACK);
mPaintPoint.setStrokeWidth(10);
mPaintPoint.setStyle(Paint.Style.FILL);
mPaintPoint.setAntiAlias(true);
//画圆画笔
mPaintBezier=newPaint();
mPaintBezier.setStyle(Paint.Style.STROKE);
mPaintBezier.setColor(Color.RED);
mPaintBezier.setStrokeWidth(5);
mPaintBezier.setAntiAlias(true);
//初始化数据点
mPointDatas=newArrayList<>();
//初始化控制点
mPointControlls=newArrayList<>();
}
@Override
protected voidonSizeChanged(intw,inth,intoldw,intoldh) {
//测量View宽高
viewWidth=w;
viewHigh=h;
//获取View中心点
mCentreX=viewWidth/2;
mCentreY=viewHigh/2;
//添加数据点
mPointDatas.add(newPointF(mCentreX,mCentreY-mControlRadius));
mPointDatas.add(newPointF(mCentreX+mControlRadius,mCentreY));
mPointDatas.add(newPointF(mCentreX,mCentreY+mControlRadius));
mPointDatas.add(newPointF(mCentreX-mControlRadius,mCentreY));
//添加控制点
mPointControlls.add(newPointF(mCentreX+mControlRadius*stu,mCentreY-mControlRadius));
mPointControlls.add(newPointF(mCentreX+mControlRadius,mCentreY-mControlRadius*stu));
mPointControlls.add(newPointF(mCentreX+mControlRadius,mCentreY+mControlRadius*stu));
mPointControlls.add(newPointF(mCentreX+mControlRadius*stu,mCentreY+mControlRadius));
mPointControlls.add(newPointF(mCentreX-mControlRadius*stu,mCentreY+mControlRadius));
mPointControlls.add(newPointF(mCentreX-mControlRadius,mCentreY+mControlRadius*stu));
mPointControlls.add(newPointF(mCentreX-mControlRadius,mCentreY-mControlRadius*stu));
mPointControlls.add(newPointF(mCentreX-mControlRadius*stu,mCentreY-mControlRadius));
super.onSizeChanged(w,h,oldw,oldh);
}
@Override
protected voidonDraw(Canvascanvas) {
super.onDraw(canvas);
//画坐标
canvas.drawLine(0,mCentreY,viewWidth,mCentreY,mCoordinatePaint);
canvas.drawLine(mCentreX,0,mCentreX,viewHigh,mCoordinatePaint);
//画数据点4个
for(inti =0; i
canvas.drawPoint(mPointDatas.get(i).x,mPointDatas.get(i).y,mPaintPoint);
}
//画控制点8个
for(inti =0; i
canvas.drawPoint(mPointControlls.get(i).x,mPointControlls.get(i).y,mPaintPoint);
}
//贝塞尔三阶画圆
for(inti =0; i
if(i < (mPointDatas.size() -1)) {
Pathpath =newPath();
path.moveTo(mPointDatas.get(i).x,mPointDatas.get(i).y);
path.cubicTo(mPointControlls.get(i*2).x,mPointControlls.get(i*2).y,mPointControlls.get(i*2+1).x,mPointControlls.get(i*2+1).y,
mPointDatas.get(i+1).x,mPointDatas.get(i+1).y);
//绘制路径
canvas.drawPath(path,mPaintBezier);
}else{
Pathpath =newPath();
path.moveTo(mPointDatas.get(i).x,mPointDatas.get(i).y);
path.cubicTo(mPointControlls.get(i*2).x,mPointControlls.get(i*2).y,mPointControlls.get(i*2+1).x,mPointControlls.get(i*2+1).y,
mPointDatas.get(0).x,mPointDatas.get(0).y);
//绘制路径
canvas.drawPath(path,mPaintBezier);
}
}
}
public voidstart(intchangeType){
this.changeType=changeType;
handler.postDelayed(runnable,1000);
}
Handlerhandler=newHandler();
Runnablerunnable=newRunnable() {
@Override
public voidrun() {
if(changeType==0) {//圆变化成心
if(count*rate<100) {
mPointDatas.get(0).y=mPointDatas.get(0).y+1f*rate;
mPointControlls.get(2).x=mPointControlls.get(2).x-0.2f*rate;
mPointControlls.get(3).y=mPointControlls.get(3).y-0.8f*rate;
mPointControlls.get(4).y=mPointControlls.get(4).y-0.8f*rate;
mPointControlls.get(5).x=mPointControlls.get(5).x+0.2f*rate;
invalidate();
count++;
handler.postDelayed(this,50);
}
}else if(changeType==1){//四叶草
if(count*rate<200) {
mPointDatas.get(0).y=mPointDatas.get(0).y+1f*rate;
mPointDatas.get(1).x=mPointDatas.get(1).x-1f*rate;
mPointDatas.get(2).y=mPointDatas.get(2).y-1f*rate;
mPointDatas.get(3).x=mPointDatas.get(3).x+1f*rate;
invalidate();
count++;
handler.postDelayed(this,100);
}
}else if(changeType==2){//水滴
if(count*rate<100) {
mPointDatas.get(0).y=mPointDatas.get(0).y-1f*rate;
mPointDatas.get(1).x=mPointDatas.get(1).x-0.35f*rate;
mPointDatas.get(3).x=mPointDatas.get(3).x+0.35f*rate;
for(inti =0; i
if(i ==0|| i ==1|| i ==6|| i ==7) {
if(mPointControlls.get(i).x>mCentreX) {
mPointControlls.get(i).x=mPointControlls.get(i).x-0.4f*rate;
}else{
mPointControlls.get(i).x=mPointControlls.get(i).x+0.4f*rate;
}
if(mPointControlls.get(i).y>mCentreY) {
mPointControlls.get(i).y=mPointControlls.get(i).y-0.4f*rate;
}else{
mPointControlls.get(i).y=mPointControlls.get(i).y+0.4f*rate;
}
}else if(i ==2|| i ==3|| i ==4|| i ==5) {
if(mPointControlls.get(i).x>mCentreX) {
mPointControlls.get(i).x=mPointControlls.get(i).x-0.2f*rate;
}else{
mPointControlls.get(i).x=mPointControlls.get(i).x+0.2f*rate;
}
if(mPointControlls.get(i).y>mCentreY) {
mPointControlls.get(i).y=mPointControlls.get(i).y-0.2f*rate;
}else{
mPointControlls.get(i).y=mPointControlls.get(i).y+0.2f*rate;
}
}
}
invalidate();
count++;
handler.postDelayed(this,100);
}
}
}
};
本来想明天在弄好源码上传,想想还是立马上传了,源码里还有其它两个简单贝塞尔曲线例子,用以入门学习。
源码下载
下一期将发表个我自己实现的,Android FrameLayout+ViewDragHelper实现QQ7.1.0侧滑菜单,提意见,谢谢!