接机器学习之逻辑回归(1),尝试判别分析和多元自适应回归样条方法对数据集的预测能力。
线性判别分析即LDA,可通过MASS包实现,语法和lm()与glm()相似。
lda.fit <- lda(class~.,data = train)
lda.fit
Call:
lda(class ~ ., data = train)
Prior probabilities of groups:
benign malignant
0.6462 0.3538
Group means:
V1 V2 V3 V4 V5 V6 V7 V8 V9
benign 3.007 1.348 1.410 1.374 2.125 1.334 2.131 1.298 1.079
malignant 7.084 6.503 6.533 5.557 5.263 7.713 5.850 5.898 2.904
Coefficients of linear discriminants:
LD1
V1 0.189076
V2 0.107205
V3 0.081504
V4 0.032985
V5 0.100915
V6 0.268742
V7 0.112070
V8 0.080503
V9 0.004782
良性概率大约为64%,恶性概率大约为36,我们可以使用plot()函数,画出判别评分的直方图和密度图。
可以看出,组间有些重合,这表明有些预测被错误分类。
提取良性和恶性其中一列
train.lad.fit0 <- predict(lda.fit,type = "response")$posterior[,2]
train.lad.fit <- ifelse(train.lad.fit0>=0.5,1,0)
misClassError(trainY,train.lad.fit)
[1] 0.0424
confusionMatrix(trainY,train.lad.fit)
0 1
0 298 13
1 7 154
lda在测试集上表现比训练集好得多。
test.lda.probs0 <- predict(lda.fit,newdata = test)$posterior[,2]
test.lda.probs <- ifelse(test.lda.probs0>=0.5,1,0)
misClassError(testY,test.lda.fit)
[1] 0.0284
confusionMatrix(testY,test.lda.fit)
0 1
0 138 5
1 1 67
下面用二次判别分析(QDA)模型来拟合一下数据。
qda.fit <- qda(class~.,data = train)
test.qda.probs0 <- predict(qda.fit,newdata = test)$posterior[,2]
test.qda.probs <- ifelse(test.qda.probs0>=0.5,1,0)
misClassError(testY,qda.fit.probs)
[1] 0.0237
confusionMatrix(testY,qda.fit.probs)
0 1
0 135 1
1 4 71
看起来QDA模型准确率最高。再用多元自适应回归样条方法拟合一下模型。
(pmothod ="cv",nfold=5),五折交叉验证
(ncross=3),重复3次
(degree=1),使用没有交互项的加法
(minspan=-1),每个输入特征指使用一个铰链函数
library(earth)
set.seed(1)
earth.fit <- earth(class~.,data = train,pmethod = "cv",nfold = 5,ncross = 3,degree = 1,minspan=-1,glm = list(family=binomial))
summary(earth.fit)
Call: earth(formula=class~., data=train, pmethod="cv", glm=list(family=binomial),
degree=1, nfold=5, ncross=3, minspan=-1)
GLM coefficients
malignant
(Intercept) -5.6101
V2 0.0020
V3 0.3348
V6 0.3915
V8 0.1398
h(V1-3) 0.6547
h(V5-2) 0.2609
h(3-V7) -1.1045
h(V7-3) 0.3524
Earth selected 9 of 11 terms, and 7 of 9 predictors using pmethod="cv"
Termination condition: RSq changed by less than 0.001 at 11 terms
Importance: V6, V2, V1, V8, V7, V5, V3, V4-unused, V9-unused
Number of terms at each degree of interaction: 1 8 (additive model)
Earth GRSq 0.8271 RSq 0.8387 mean.oof.RSq 0.825 (sd 0.0322)
GLM null.deviance 613.4 (471 dof) deviance 85.3 (463 dof) iters 8
pmethod="backward" would have selected:
8 terms 7 preds, GRSq 0.8273 RSq 0.8374 mean.oof.RSq 0.8232
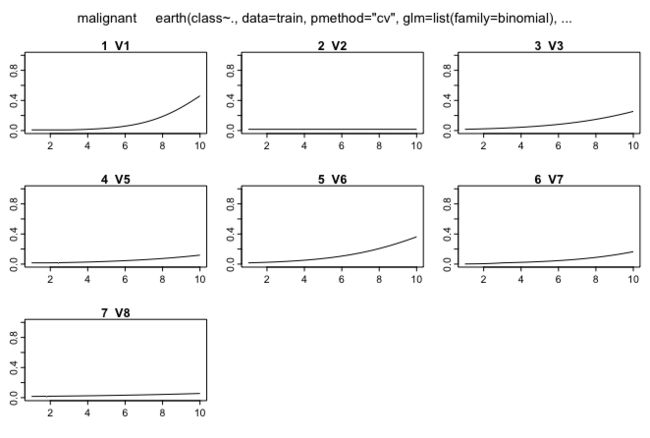
plot()函数可以画出控制其他变量保持不变,某个预测变量发生变化时,响应变量发生的改变。
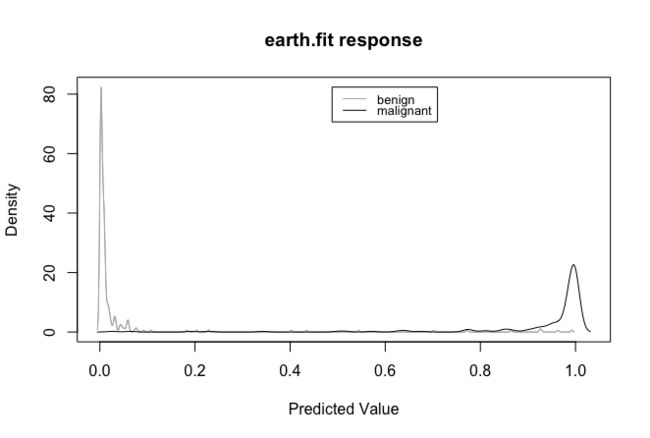
通过plotd()函数,可以生成按类别标签分类的预测概率密度图。
下面看看变量之间的相对重要性。
nsubsets是精简过程完成后包含这个变量的模型的个数
gcv和rss列是这个变量贡献减少量
evimp(earth.fit)
nsubsets gcv rss
V6 8 100.0 100.0
V2 7 41.4 42.3
V1 6 22.3 24.2
V8 5 13.4 16.1
V7 4 9.2 12.2
V5 3 6.0 9.2
V3 2 0.7 5.9
再看下模型在测试集上的表现。
test.earth.probs0 <- predict(earth.fit,newdata = test,type = "response")
test.earth.probs <- ifelse(test.earth.probs0>=0.5,1,0)
misClassError(testY,test.earth.probs)
[1] 0.0284
confusionMatrix(testY,test.earth.probs)
0 1
0 137 4
1 2 68
4、模型选择
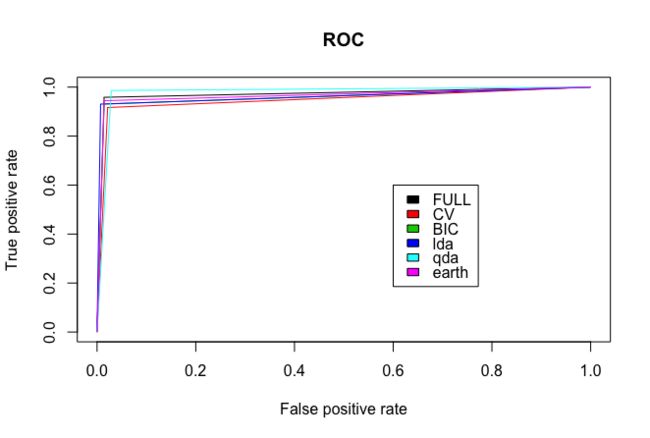
绘制ROC图
library(ROCR)
pred.full <- prediction(test.probs,testclass)
perf.cv <- performance(pred.cv,"tpr","fpr")
plot(perf.cv,main="ROC",col=2,add=TRUE)
pred.bic <- prediction(test.bic.probs,testclass)
perf.lda <- performance(pred.lda,"tpr","fpr")
plot(perf.lda,main="ROC",col=4,add=TRUE)
pred.qda <- prediction(test.qda.probs,testclass)
perf.earth <- performance(pred.earth,"tpr","fpr")
plot(perf.earth,main="ROC",col=6,add=TRUE)
legend(0.6,0.6,c("FULL","CV","BIC","lda","qda","earth"),1:6)
计算AUC值
performance(pred.full,"auc")@y.values
performance(pred.cv,"auc")@y.values
performance(pred.bic,"auc")@y.values
performance(pred.lda,"auc")@y.values
performance(pred.qda,"auc")@y.values
performance(pred.earth,"auc")@y.values
performance(pred.full,"auc")@y.values
[[1]]
[1] 0.972
performance(pred.cv,"auc")@y.values
[[1]]
[1] 0.9475
performance(pred.bic,"auc")@y.values
[[1]]
[1] 0.9581
performance(pred.lda,"auc")@y.values
[[1]]
[1] 0.9617
performance(pred.qda,"auc")@y.values
[[1]]
[1] 0.9787
performance(pred.earth,"auc")@y.values
[[1]]
[1] 0.965
从结果上看来,qda模型准确率最高,最终选用哪个模型,我们可以权衡模型的准确性与解释性,或者简约性与扩展性。选择之前,我们还可以将训练集和测试集重新随机化,再做一遍分析,比如50/50划分,60/40划分,80/20划分,然后采用最稳定的模型。