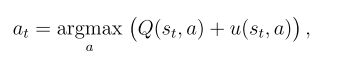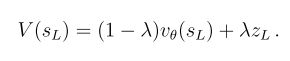2016年 AlphaGo 横空出世,在AI界和围棋界掀起了一阵腥风血雨。宝刀一出,无数围棋高手如樊麾,李世石,柯洁等人先后被斩于马下。
正所谓:十步杀一人,千里不留行。事了拂衣去,深藏功与名。
AlphaGo 使用的技术有深度神经网络和树搜索,这篇文章主要介绍一下树搜索。
简单的说 Monte-Carlo Tree Search(MCTS)的意思就是讲蒙特卡罗抽样的思想用到树搜索上。在我了解到MCTS思想背后的简单和暴力之后,在棋类领域机器打败人类是必然的事情。但我认为这仅仅能说明机器的计算水平很高,这是AI领域进步的一小步,现在的AI离真正的智能还很远。
[2016, Mastering the game of Go with deep neural networks and tree search - DeepMind]
对于人工智能来说,围棋一直被视为最具挑战性的经典游戏,这是由于其巨大的搜索空间以及难于评估的棋盘盘面和走子。这里我们介绍了一个新方法:使用价值网络 (value networks )来评估棋盘盘面和使用策略网络 (policy networks )来选择走子。为了训练这些深度神经网络,我们将有监督学习(从人类职业比赛中学习)和增强学习(从自我对抗的比赛中学习)创新地结合在一起。在没有使用任何前瞻搜索的情况下,这些神经网络的水平已经相当于最先进的使用蒙特卡罗树搜索(MCTS: Monte Carlo tree search)的程序,这些程序模拟了成千上万的随机的自我对抗盘局。我们还提出了一种将蒙特卡罗仿真和价值网络以及策略网络结合起来的新搜索算法。使用该搜索算法后, AlphaGo 在和其他围棋程序的对弈中,赢了 99.8%的盘局,并且以 5 比 0 击败了欧洲围棋冠军。这是计算机程序首次在全尺寸的围棋对抗中击败职业围棋选手,这个壮举以前被认为是至少十年以后才会发生。
[知乎]Alphago打败的可不是李世石抑或全人类,而是围棋这项智力运动千百年来演变发展积攒而出的人类自信。
多臂赌博机问题
这里又要介绍一个新的概念了:Multi-Arm Bandit Problem 多臂赌博机问题。
设想我们身处在一个赌城中,面前是多台赌博机,但我们不知道每台赌博机输或者赢的概率。那我们怎么能在给定一定的次数,例如玩100次,获得最大的收益呢?
本能的最简单想法是,我们将每台机器都试w次(例如10次),统计每台机器拉动10次拉杆的最终收益,选择收益最大的拉杆一直拉。。。
那么请问这样的做法是能保证最大收益么? 实际上这是一个两难的境地(exploration-exploitation),一方面我们要尝试了解哪台机器会有最大的收益,另一方面我们要牺牲潜在的收益来多尝试。
以上就是多臂赌博机问题。
马尔可夫决策过程
我们要求解的问题是Markov Decision Processes(马尔可夫决策过程)。
什么是Markov Decision Processes呢?
MDPs
An MDP has four components: S, A, Pr, Pt :
- finite state set S
- finite action set A
- Transition distribution Pr(s’ | s, a)
Probability of going to state s’ after taking action a in state s
First-order Markov model - Bounded reward distribution Pr(r | s, a)
Probability of receiving immediate reward r after taking action a in state s
First-order Markov model
给定一个MDP,我们希望计算出一个策略,计算这个策略可以是online或者offline的。
一个策略是状态到动作的随机映射。
π:S → A
π(s) is action to do at state s
specifies a continuously reactive controller
怎么衡量策略的好坏呢?
我们实际上是使用一个值函数,最优的策略是所有状态获得回报(reward)最大的那个策略。
MDP问题规模比较小的时候,可以使用值迭代或者策略迭代求解。
但我们对有指数级别的状态空间的MDP问题感兴趣。传统的方法对于这类问题就无能为力了。例如象棋,围棋。
蒙特卡罗与马尔可夫决策过程
蒙特卡罗思想即抽样的思想深深的影响了各个领域。那么我们可以用抽样的思想求解MDPs问题么?
是的,我们可以。
不是状态空间大么? 我们用随机模拟的思想求解MDP。
前后提出了以下算法:
UniformBandit Algorithm
UniformBandit Algorithm (NaiveBandit from [Even-Dar et. al., 2002])在2002年,提出了朴素赌博机算法。
思想:
- 拉动每个拉杆w次
-
返回平均奖励最大的拉杆
Policy Rollout Algorithm
思想:
- 对于每个动作,执行simQ w次
- 选择平均奖励最大的simQ对应的动作。
Multi-Stage Rollout
篇幅原因,不做详细介绍。
总结一下上面的算法,虽然好用,但是效率不高,也不能保证最优或者接近最优。
接下来有人提出了Sparse Sampling 算法。
Sparse Sampling
是Kearns在2002年提出的,这个算法是可以保证最优的。
但是这个算法的问题是建立的搜索树是指数级增长的。
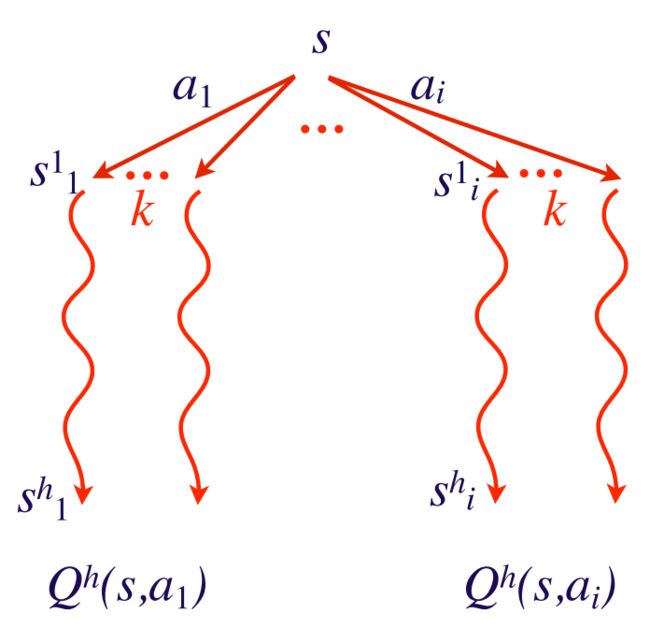
Each state generates kw new states
(w states for each of k bandits)
• Total # of states in tree (kw)^h
好消息
这个算法振奋人心的是我们可以获得近似最优,同时这个规划算法的运行时间不依赖于状态空间的大小!坏消息
但是搜索树值指数级的。实际应用
我们使用较小的h。降低指数级的增长。
Sparse Sampling 不太好用的原因是,它浪费掉时间探索树前景不好的部分。它把资源都平均的分配给了每一个状态。
我们能否平衡exploitation 和 exploration呢?
UCB1算法
在2002年Auer提出了 UCB1 算法解决多臂赌博机问题。
UCB1(Upper Confidence Bound)上置信区间,这是概率论中的一个概念,意思是估计未知参数的可信程度,以区间的形式给出。有时我们仅仅关心上限或者下限。这就提出了单侧置信上限或者下限的概念。
简单的说这个算法,平衡了exploitation 和 exploration。在保证一定收益的同时,又不放弃潜在的收益。
UCT算法
在2006年Kocsis & Szepesvári提出了将UCB1的思想用在解决树搜索的想法,提出了UCT(Upper Confidence with Tree-based Search)。
算法图中的常数C是一个经验值,根据实际可以进行调整。
之前的抽样算法没有提出抽样的策略,对应于一个状态可用的每个动作都是随机抽样执行的。一个好的抽样策略应该进一步探索有前景的动作,和剪枝不好的动作。
蒙特卡洛树搜索(MCTS: Monte-Carlo tree search)利用蒙特卡洛 rollouts 来评估每个盘面在搜索树中的值。运行越多的仿真,搜索树变得越大,相对值也越准确。用于在搜索过程选择动作的策略也随着时间推移而提高,该策略是通过选择有更高值的子树实现的。逐渐地,策略收敛到最优方案,评估也收敛到最优值函数。目前最强的围棋程序是基于MCTS 的,并通过训练成能预测专业选手的走子来得以加强 。这些策略用于将搜索收窄到一束最有可能的动作,并在下棋时采样动作。该方法达到了很高的业余选手的水平。但是,这些以前的工作局限于肤浅的策略,或值函数是基于输入特征的线性组合 。
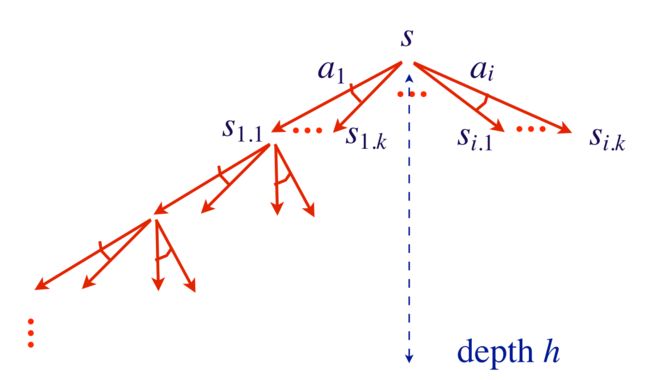
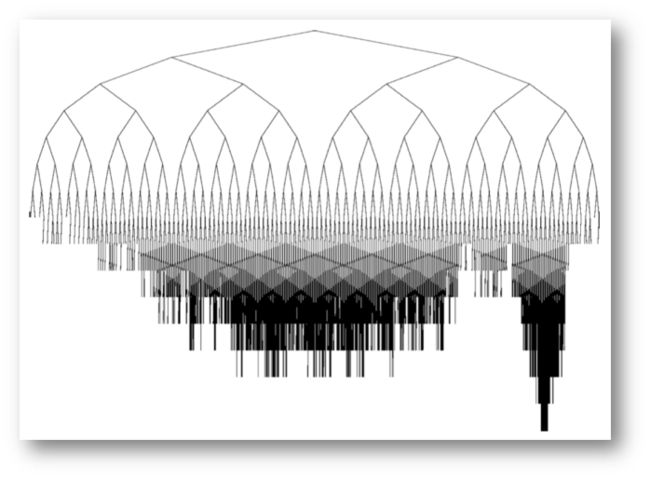
UCT建立的搜索树如下:
UCT的重点是:
在2006年以后,学者又陆续提出了UCT算法的很多改进。这里先不做介绍了。UCT的来源和主要思想在这篇文章中已经介绍清楚了。
AlphaGo 与 MCTS
AlphaGo基于深度神经网络和MCTS在围棋领域打败了人类世界冠军。下面简要介绍一下这是如何实现的。
在围棋领域仅仅通过使用MCTS算法,因为问题的复杂性,在水平上是超过打败人类的。我认为在围棋领域通过深度神经网络和MCTS的结合有效减少了搜索时间。
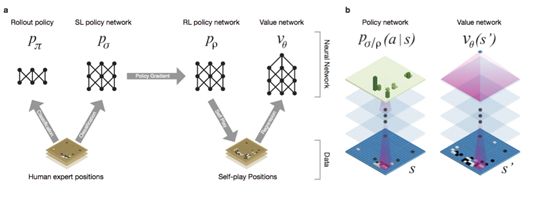
1 Supervised Learning of Policy Networks
使用有监督学习训练策略网络。策略网络输出的是落子的概率分布。该网络预测专业选手走子的准确率为57.7%
2 Reinforcement Learning of Policy Networks
使用强化学习改善第一步训练的策略网络。使用RL策略和SL策略网络对抗时,RL策略网络赢得了80%的棋局。
3 Reinforcement Learning of Value Networks
价值网络的增强学习。
训练最后一步关注盘面落子的评估,估计一个值函数来预测盘面s的结果。价值网络和策略网络的架构类似,但输出的是一个预测,而非概率分布。
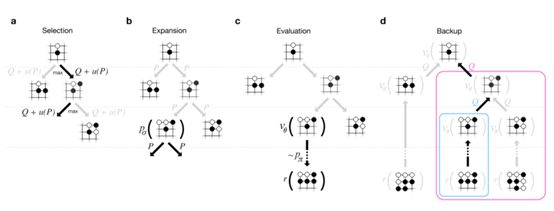
4 Searching with Policy and Value Networks
AlphaGo将策略和价值网络结合到MCTS算法。
当前盘面的下一落子的盘面位置SL,由策略网络处理,得到先验概率,叶节点价值的估计由价值网络和随机仿真决定。
结语
近年来围棋领域最大的突破是MCTS思想的引入。
对于人工智能来说,围棋在许多方面都是经典的难题:富有挑战的决策任务,棘手的搜索空间等等。
在2016年的Mastering the game of Go with deep neural networks and tree search - DeepMind一文中,提出了策略或值函数直接进行近似估值似乎不可行,提出了策略网络以及价值网络结合的思想。
基于这个思想AlphaGo 最终达到了围棋的职业水准,这也给其他看起来不可触及的人工智能领域达到人类的水平带来了希望。
启示
基于计算机视觉的深度神经网络和蒙特卡洛树搜索,终于在围棋领域打败的人类。
给我们的启示是关于搜索问题,我们还能否提出更加优秀的算法?
参考资料
[1] 概率论与数理统计
[2] L. Kocsis and C. Szepesvári, “Bandit based monte-carlo planning,” Proc. ECML, pp. 282–203, 2006.
[3] C. B. Browne et al., “A Survey of Monte Carlo Tree Search Methods,” Comput. Intell. AI Games, IEEE Trans., vol. 4, no. 1, pp. 1–43, 2012
[4] CS188: Artificial Intelligence https://edge.edx.org/courses/course-v1:Berkeley+CS188+SP17/info
[5] Monte-Carlo Planning: Basic Principles and Recent Progress http://videolectures.net/icaps2010_fern_mcpbprp/
[6] S. Sanner, “Relational dynamic influence diagram language (rddl): Language description,” Unpubl. ms. Aust. Natl. Univ., 2010.
[7] S. J. Russell and N. Peter, Artificial Intelligence A Modern Approach.pdf.
[8] D. Silver et al., “2016 - Mastering the game of Go with deep neural networks and tree search - DeepMind nature16961,” Nature, vol. 529, no. 7587, pp. 484–489, 2016.