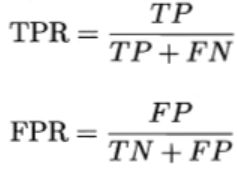1、分类结果混淆矩阵
对于二分类问题,可将样例根据其真实类别与学习期预测类别的组合划分为真正例(True Positive),假正例(False Positive),真反例(True Negative),假反例(False Negative)四种情形,四种情形组成的混淆矩阵如下:
| 真实情况 | 预测结果 | |
|---|---|---|
| 正例 | 反例 | |
| 正例 | TP | FN |
| 反例 | FP | TN |
2、P-R曲线
P-R曲线刻画查准率和查全率之间的关系,查准率指的是在所有预测为正例的数据中,真正例所占的比例,查全率是指预测为真正例的数据占所有正例数据的比例。
即:查准率P=TP/(TP + FP) 查全率=TP/(TP+FN)
查准率和查全率是一对矛盾的度量,一般来说,查准率高时,查全率往往偏低,查全率高时,查准率往往偏低,例如,若希望将好瓜尽可能多选出来,则可通过增加选瓜的数量来实现,如果希望将所有的西瓜都选上,那么所有的好瓜必然都被选上了,但这样查准率就会较低;若希望选出的瓜中好瓜比例尽可能高,则可只挑选最有把握的瓜,但这样就难免会漏掉不少好瓜,使得查全率较低。
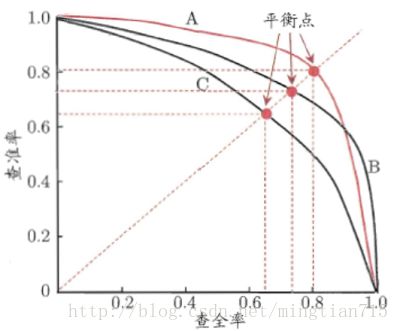
在很多情况下,我们可以根据学习器的预测结果对样例进行排序,排在前面的是学习器认为最可能是正例的样本,排在后面的是学习器认为最不可能是正例的样本,按此顺序逐个把样本作为正例进行预测,则每次可计算当前的查全率和查准率,以查准率为y轴,以查全率为x轴,可以画出下面的P-R曲线。
如果一个学习器的P-R曲线被另一个学习器的P-R曲线完全包住,则可断言后者的性能优于前者,例如上面的A和B优于学习器C,但是A和B的性能无法直接判断,但我们往往仍希望把学习器A和学习器B进行一个比较,我们可以根据曲线下方的面积大小来进行比较,但更常用的是平衡点或者是F1值。平衡点(BEP)是查准率=查全率时的取值,如果这个值较大,则说明学习器的性能较好。而F1 = 2 * P * R /( P + R ),同样,F1值越大,我们可以认为该学习器的性能较好。
3、ROC曲线
很多学习器是为测试样本产生一个实值或概率预测,然后将这个预测值与一个分类阈值进行比较,若大于阈值分为正类,否则为反类,因此分类过程可以看作选取一个截断点。
不同任务中,可以选择不同截断点,若更注重”查准率”,应选择排序中靠前位置进行截断,反之若注重”查全率”,则选择靠后位置截断。因此排序本身质量的好坏,可以直接导致学习器不同泛化性能好坏,ROC曲线则是从这个角度出发来研究学习器的工具。
曲线的坐标分别为真正例率(TPR)和假正例率(FPR),定义如下:
下图为ROC曲线示意图,因现实任务中通常利用有限个测试样例来绘制ROC图,因此应为无法产生光滑曲线,如右图所示。
绘图过程很简单:给定m个正例子,n个反例子,根据学习器预测结果进行排序,先把分类阈值设为最大,使得所有例子均预测为反例,此时TPR和FPR均为0,在(0,0)处标记一个点,再将分类阈值依次设为每个样例的预测值,即依次将每个例子划分为正例。设前一个坐标为(x,y),若当前为真正例,对应标记点为(x,y+1/m),若当前为假正例,则标记点为(x+1/n,y),然后依次连接各点。
下面举个绘图例子: 有10个样例子,5个正例子,5个反例子。有两个学习器A,B,分别对10个例子进行预测,按照预测的值(这里就不具体列了)从高到低排序结果如下:
A:[反正正正反反正正反反]
B : [反正反反反正正正正反]
按照绘图过程,可以得到学习器对应的ROC曲线点
A:y:[0,0,0.2,0.4,0.6,0.6,0.6,0.8,1,1,1]
x:[0,0.2,0.2,0.2,0.2,0.4,0.6,0.6,0.6,0.8,1]
B:y:[0,0,0.2,0.2,0.2,0.2,0.4,0.6,0.8,1,1]
x:[0,0.2,0.2,0.4,0.6,0.8,0.8,0.8,0.8,0.8,1]
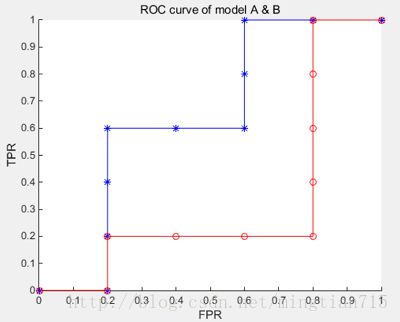
绘制曲线结果如下:
蓝色为学习器A的ROC曲线,其包含了B的曲线,说明它性能更优秀,这点从A,B对10个例子的排序结果显然是能看出来的,A中正例排序高的数目多于B。此外,如果两个曲线有交叉,则需要计算曲线围住的面积(AUC)来评价性能优劣。
4、第一章知识点拾遗
假设空间:我们把学习过程看作一个在所有假设组成的空间中进行搜索的过程,搜索目标是找到与训练集匹配的假设。拿书中的例子来说,我们通过色泽、根蒂、敲声来判断瓜的好坏,色泽有两种取值,根蒂有三种取值,敲声有两种取值,那么总共的假设空间有4 * 3 * 3 + 1 = 37 种,即我们训练的目标是从这37种假设中找到与训练样本最为匹配的假设。当然匹配到的假设可能有多种,这时候就会用到归纳偏好。
归纳偏好:给定一组西瓜的训练集,我们通过训练样本的训练发现有三个能够与其相匹配的假设,那么到底选择哪一个呢?这时,学习算法本身的偏好就会起到关键的作用。我们可能喜欢更复杂的模型,也可能喜欢更简单的模型。机器学习算法在学习过程中对某种类型假设的偏好,称为归纳偏好。
奥卡姆剃刀:这是一种常用的、自然科学研究中最基本的原则,即“若有多个假设与观察一致,则选择最简单的一个”。
5、第二章知识点拾遗
数据集拆分:如果我们有一个数据集D,如果我们想用这个数据集既用来训练,又用来测试,我们应该如何做呢?有下面几种做法:
1)留出法:直接将数据集D拆分为两个互斥的集合,其中一个用作训练集,另一个用作测试集。单次使用留出法得到的估计结果往往不够稳定可靠,在使用留出法时,一般要采用若干次随机划分,重复进行试验评估后取平均值作为留出法的评估结果。
2)交叉验证法,大家都比较熟悉,一般称为k折交叉验证,如果k的大小与数据集大小m相同,此时又称为留一法,留一法的评估结果往往被认为比较准确,然后,留一法也有缺陷,在数据集比较大的时候,计算复杂度太高
3)自助法:通过有放回的随机抽样不断产生与原数据集大小相同的数据集D‘,然后没有在D’中出现过的数据组合为测试集。自助法在数据集较小,难以有效划分训练/测试集的时候比较有用。