优秀应用算法都大量用到位运算,而位运算在工作中很少用到,大多数教材只会教大家二进制和十进制如何互换,都是死记硬背式的,并没有去讲解真正含义,换一个进制之后,依然不会,我们回到最根本的一些计数方法上,从10进制来推算,希望用一种更简单的方式介绍其原理。
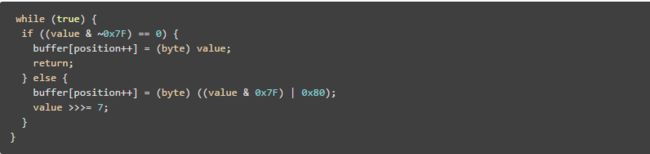
我们来看上一篇的一个Varint算法,这个算法的目的是为了令一个整型占用更少的字节,比如小于127的数字,只需占用一个字节即可,小于16384的数字,采用2个字节即可。算法如下:
我们来看看具体图例:
我们看到在小于2097153期间,占用空间会小于4个字节,这个优势还比较明显,不过也有弊端,比如超过268435456之后会有占用5个字节,考虑到大多数情况下,并不会应用到这么大的数字,优化空间方面还是不错的。
通过上述算法实现,我发现优秀的应用算法都会大量用到了位运算,而位运算在工作中却很少用到。位运算速度要快于整数运算的,特别是整数乘法,需要10个或者更多个时钟,若果采用移位操作一个或者2个时钟就够了,不过由于我们常采用十进制来进行算术运算,对二进制的位运算不够熟悉,阅读起来会比较耗费精力,所以借助上述算法实现,我们分析一下位运算的优势以及应用,从而更好的理解二进制。上述代码中,有运用到移位操作,位运算,字节序等相关知识点,我们一一分析。
进位制
我们知道,计算机的存储和处理的信息都是以二进制的,虽然在编写程序的期间数运算还是采用10进制表示,但到机器执行的时候,还会以2进制来进行处理。对于有10个指头的人来说,熟知10进制是很自然的事情,你看教小孩子数学的时候,都是先从数指头开始的,那么若是我们只有2个指头,是不是我们现在会更好理解二进制了?
其他进制转换10进制
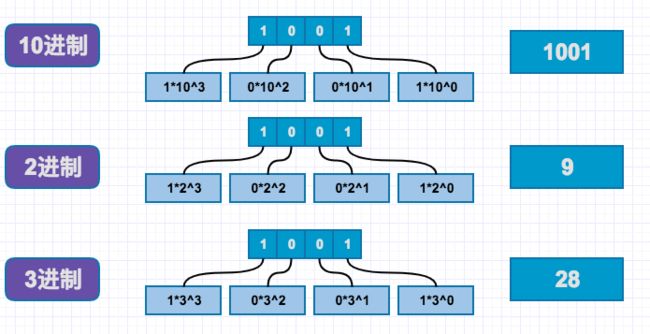
大多数教材会教大家二进制和十进制如何互换,但多数说都是死记硬背式的,并没有去讲解真正含义,换一个进制之后,依然不会,我们回到最根本的一些计数方法上,从10进制来推算。比如我们看一个数字1001,采用十进制表示是:1x10^3+0*10^2+0*10^1+1*10^0。首先从右往左,我们可以看成是从低位到高位,每高一位,指数+1,其次10进制是以10为底数,其三这个公式是采用10进制算术进行计算的(用什么进制算出答案就相当于把当前进制转换为了什么进制了)。这个方式适合所有的进制转换,理解了这个,后续的进制转换都会很容易理解。
2进制的比较简单,我们直接忽略,我们来看下应用到3进制,同样是1001,转换10进制公式:1x3^3+0*3^2+0*3^1+1*3^0=28,我们发现只是底数改变,因为是3进制,所以以3为底数,另外计算方式还是采用10进制算式计算,这表明用10进制算出的答案,就相当于3进制转换为10进制,1001转换为10进制就是28。
那为何不采用其他进制来计算?采用其他进制计算,那么其他进制的乘法口诀你的熟练一遍了,比如10进制的99乘法口诀,你用其他进制的乘法口诀得自己来演绎一遍了,如此这个和我们的常用习惯有些相驳,换算起来会比较慢,所以一般采用十进制与其它进制互转或者作为中间步骤来处理。
10进制转换为其他进制
采用上述方法后,我们已经可以做到所有进制转换,包括10进制转3进制,比如十进制28转换为3进制28=2*3+22,这个采用3进制(3的三进制表示10)来进行计算,但是会很麻烦。所以10进制转换其他进制,我们常采用短除法,如下:
当前数不断除以3并把余数作为新的最高位,28除以3余1,1为“个位”,9除以3余0,0为“十位”,3除以3余0,0为“百位”,最终的1是“千位”。如果我们有注意到前面的3进制转10进制算法,我们可以发现短除法其实是3进制转10进制的逆操作,比如3进制转换为十进制时候是:1*3^3+0*3^2+0*3^1+1*3^0 ,我们转换一下是((1*3+0)*3+0)*3+1,如此和10进制转换3进制的时候逆向操作。
小数
如果前面的理解了,小数就可以很容易理解了,我们还是先从10进制来看。比如十进制12.34,我们看小数后面十分位部分.3,表示把1分为10份只取3份,.04百分位部分是把1分为100份,取4份。那么我们换成公式:
我们看到小数部分还是以进制为底数,不过指数部分采用了负数,点的左边的位的指数是位的正幂,点数的右边是位的指数负幂。理解了这个,其他进制的小数部分也就了解, 它们是相同的,比如二进制1001.101:
有了这个理解,我们后续的浮点数就比较好理解了,IEEE浮点表示浮点数,也是基于这种方式,只是定义了些规范,后续我们会详细了解。
移位操作
常见的移位操作有三种:左移,逻辑右移,算术右移。
移动操作
左移
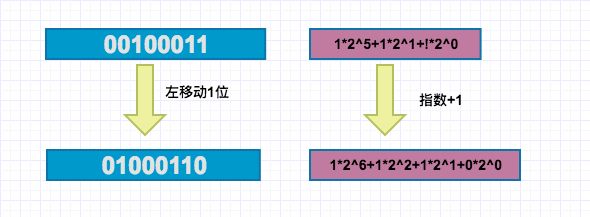
x向左移动k位,会丢弃最高的k位,并在右端补k个0,也就是常说的当前值乘以2的k次方。为何是乘以2的k次方?我们看10进制的时候,某数乘以10,就是在末尾增加1个0 ,由此我们可以联想到,二进制左移一位(末尾加一个0)相当于乘以2,这个结论普遍存在于所有进位制中:k进制数的末尾加个0,相当于该数乘以k。
我们从图中可以看到,左移动一位,就相当于进位制展开式的每个指数都加1,如此移动一位,就相当于当前数(1*2^5+1*2^1+!*2^0)*2^1=1*2^6+1*2^2+1*2^1
右移
理解了左移的原理,右移动的原理也是相同的,右移k位=进位制展开式的每个指数都减k,也就是当前数除以进制的k次方。唯一不同的是分为逻辑右移和算术右移。
逻辑右移就是无符号移位,右移几位,就在左端补几个0,比如上边 Varint中每次右移7位,相应的当前数高位就会补充7个0。
算术右移动是有符号移位,和逻辑右移不同的是,算术右移是在左端补k个最高有效位的值,如此看着有些奇特,但对有符号整数数据的运算非常有用。我们知道有符号的数,首位字节,是用来表示数字的正负。负数采用补码形式来存储,比如[11100110],10进制是-26,算术右移1位之后[11110011],10进制是-13,如若不是补最高有效位的值1而是补做事0的话,右移之后就变成正数了。
字节序
单个字节并没有字节序的问题,当一个数据需要多个字节存储的时候,就会牵扯到这样的问题,这个数据的地址是什么,存储器中如何排列这些字节,是高位地址存最高有效位,还是低位地址存最高有效位。
比如一个int类型的变量,它的地址是使用字节中最小的地址,比如在存储器上的位置是0x101、0x102、0x103,它的地址是0x101,若是这个数据是一个w位的整数,位表示为[x(w-1),x(w-2)....,x1,x0],那么其中x(w-1)是最高有效位,x0是最低有效位,w若是8的倍数,位被分组成字节,那么最高有效字节是[x(w-1)...x(w-8)],最低有效字节是[x7,x6...x0]。这个也可以成为物理顺序,和我们普通人理解的存储顺序预期相符合,比如十进制也是高位(百位,10位)在地位(个位)前面。
小端法(little endian)
如果字节的逻辑顺序与物理顺序相反,也就是w的最低有效字节在前面[x7,x6....x0],最高有效字节[x(w-1)...x(w-8)]在后面,此时成为小端法(little endian)。多数intel兼容机都采用这种规则。
大端法(big endian)
如果字节的逻辑顺序与物理顺序相同,也就是w的最低有效字节[x(w-1)...x(w-8)]在前面,最高有效字节[x7,x6....x0]在后面,称为大端法(big endian),大多数IBM和Su你Microsystems的机器都是采用这种规则。
比如一个十六进制数:0x01234567,我们用大端小端法看他们在存储器上的位置。
我们可以看到大端法是比较符合我们习惯的,高位在前地位在后。
上述Varint的算法,是采用小端法来存储字节顺序的。
每次都是获取当前数据的后7个字节存储到数据流buffer里面,也就是低位字节放在buffer字节数组的前面。
----------------------------------------------end------------------------------------------------