进制间的转换原理

1、进制的介绍

在讲进制之前，我们先看一下数制的定义：用一组固定的数字和一套统一的规则来表示数目的方法称为数制。

而数制有进位计数制与非进位计数制之分。非进位计数制的数码表示的数值大小与它在数中的位置无关，这里我们不作过多的介绍。

进位计数制的数码所表示的数值大小则与它在数中所处的位置有关，常见的有二进制、十进制、十六进制，我们这里也只介绍这三种进制的转换。

进位计数制的要素：

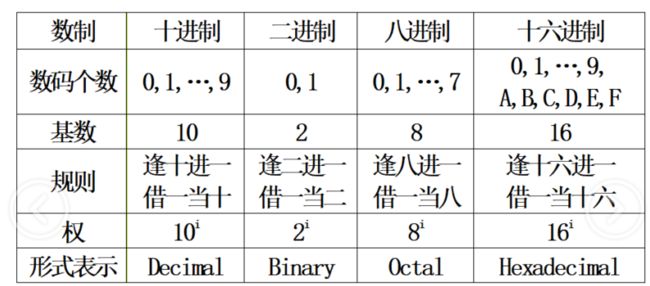
①、数码：用来表示进制数的元素。比如二进制数的数码为：0,1。十进制数的数码为：0,1,2,3,4,5,6,7,8,9。十六进制数的数码为：0,1,2,3,4,5,6,7,8,9，A,B,C,D,E,F

②、基数：数码的个数。比如二进制数的基数为2。十进制数的基数为10。十六进制数的基数为 16.

③、位权：数制中每一固定位置对应的单位值称为位权。例如十进制第2位的位权为10，第3位的位权为100；而二进制第2位的位权为2，第3位的位权为4。

那么我们可以说：每个数码所表示的数值=该数码值 * 所处位置的位权。上面的内容概括起来可以看一下下面这张图：

image.png

比如十进制数：(123)₁₀＝1×10²+2×10¹+3×10⁰
二进制数：(1010)₂ =l× 2³+0 × 2²+l× 2¹+0 × 2⁰=(10)₁₀
十六进制数：(BAD)₁₆ =11× 16²+10×16¹+13×16⁰=(2989)₁₀

2、二进制转换成其他进制

①、二进制（Binary）——>十进制（Decimal）

诀窍：从最后一 位（从右向左）开始算，依次列为第0、1、2、3………n，然后将第n位的数（0或1）乘以2的n-1次方，然后相加即可得到整数位的十进制数。

例子：将二进制数（10101）₂转化为十进制数。

②、二进制（Binary）——>十六进制（Hex）

诀窍：****因为每四位二进制数对应一位十六进制数，将二进制数从右向左每4位一隔开，不足4位的在左边用0填补即可。

例子：将二进制数（10101）₂转化为十六进制数。

3、十进制转换成其他进制

①、十进制（Decimal）——>二进制（Binary）

诀窍：****除以2，然后取每次得到的商和余数，用商继续和2相除，直到商小于2。然后把第一次得到的余数作为二进制的个位，第二次得到的余数作为二进制的十位，依次类推，最后一次得到的小于2的商作为二进制的最高位，这样由商+余数组成的数字就是转换后二进制的值（除2取余法）；

例子1：将十进制数（93）₁₀转换成二进制数。

93/2=46……….1

46/2=23……….0

23/2=11……….1

11/2=5…………1

5/2=2…………...1

2/2=1……………0

（93）₁₀=（1011101）₂

②、十进制（Decimal）——>十六进制（Hex）

　　诀窍：方法同十进制转化成二进制类似。除以16，然后取每次得到的商和余数，用商继续和16相除，直到商小于16。然后把第一次得到的余数作为十六进制的个位，第二次得到的余数作为十六进制的十位，依次类推，最后一次得到的小于16的商作为十六进制的最高位，这样由商+余数组成的数字就是转换后十六进制的值（除16取余法）

例子1：将十进制数（93）10转换成十六进制数。

93/16=5…………****13（D）

（93）10=（5D）16

4、十六进制转换成其他进制

①、十六进制（Hex）——>二进制（Binary）

诀窍：****十六进制转换成二进制与二进制转换成十六进制相反。每一位十六进制数对应四位二进制数

例子1：将十六进制数（A7）16转换成二进制数。

（A7）₁₆=（A 7）₁₆=（1010 0111）₂=（10100111）₂

②、十六进制（Hex）——>十进制（Decimal）

诀窍：方法同二进制转换成十进制类似。从最后一位（从右向左）开始算，依次列为第0、1、2、3………n，然后将第n位的数（0-9，A-F）乘以16的n-1次方，然后相 加即可得到整数位的十进制数。

例子1：将十六进制数（A7）₁₆转换成十进制数。

（A7）₁₆=（10x16¹+7x16⁰）₁₀=（160+7）₁₀=（167）₁₀