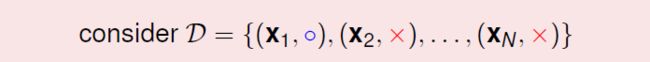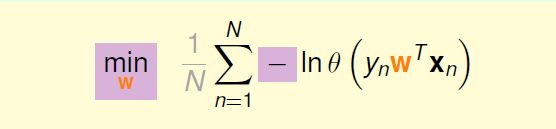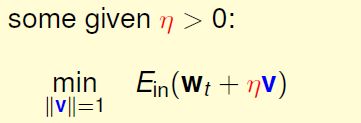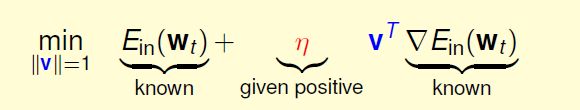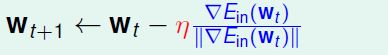Tips:符号主要参照 Lec1,部分参照其他Lec~
上一节介绍了线性回归,线性回归是输出一个 score,可以用来判断用户的信用额度等……这一节将介绍另一种 回归 算法:logistic regression 。
Lec 10:Logistic Regression
上一节线性回归的Hypothesis是 h = wx,错误衡量是 squared error ,输出是正实数集,最终的解可以通过求 pseudo-inverse 得到,简单高效。这一节要讲的回归是什么样子的呢?
1、Logistic Hypothesis
问题描述:已有病人的一些数据,例如年龄、血压、体重等等,判断病人是否患有心脏病?!这是一个我们已经很熟悉的二元分类问题。
根据前面章节可知,理想的函数 f 也是一种目标分布,在这个问题中可以写成:
为什么这样写?因为在二元分类里面关注的是 0/1 err ,所以根据概率偏向判断 0 、1 。
再看一个类似的问题:类似上一个问题,只是此时不是关注是否有心脏病,而是关注得心脏病的几率、患病的可能性是多少?!这时候,就不是binary classification了,f 应该写成:
这种情景也称为 soft binary classification ,因为此时不是直接给出确定的 0 或 1,而是给出 是 0 的概率 或 是1的概率。这就是这节要探讨的问题!
要解决这个问题,理想中的数据是什么样的?如图,没有noise的数据。当然这是不可能得到的数据。
实际中能获得的数据并没有概率值,是和做 binary classification 的时候是一样的,y 都是 患心脏病 和 没患心脏病,但是最终想得到的 target function 不一样。
这节要探讨的问题就是:target function 是输出为 [0,1] 回归函数,已知的data和之前的二元分类一样,应该如何求呢?!
先设计一下Hypothesis:
已知输入x = (x1,x2,…,xd),前面都有计算score ,这里同样是这样,先计算一个加权分数:
这样做解释的通:分数高必然风险高,分数低风险也低,如何把score转化到 [0,1] 之间呢?
这时就要用到 logistic function :θ(s),hypothesis 就是:h(x)= θ(wT x),图形为:
进一步了解下logistic function,表达式为:
并且存在一些特殊取值,与预期一致:
则,logistic regression 的 h 为:
我们要想办法用这个h(x)去逼近目标函数 f(x)= P(y|x)。
2、Likelihood & Cross-Entropy Error
前面提到过,设计一个算法,要有Hypothesis,还要有一个衡量标准Ein,然后去最优化这个衡量标准。那么LogReg的Ein是怎么样的呢?!
先回忆并对比一下三个线性模型,共同的地方是都会计算 score:s = wT x (这三个图很重要,之间的关系也很重要,后面还会多次提到)
LogReg的err定义有一种特殊的方法:Likelihood
先给出f的另一种表达方式:
现在看一组data:
考虑产生这组data的概率!(重点)
对于 f , 产生各个data的概率是:
根据图1的表达,用 f 替换 P :
由于我们希望 h 接近 f ,所以这里用 h “假装”(取代) f ,对于 h ,产生各个data的概率(可能性,likelihood)是:
现在想想,如果 h 接近 f,那么 h 产生这些data的 likelihood 也应该接近 f 产生这些data的概率;并且 f 产生这些 data的几率通常很大(恩,这是当然了,data就是从f那来的,只不过会存在一些noise干扰)。
所以!就得到一个特别的 error measure ,我们希望最大化 likelihood(h)!
给出一个关于 h(x)= θ(wT x)的性质:对称性,即 1 - h(x)= h(-x),根据 θ 函数图形也可以看出,不解释。
这时, likelihood(h)可以写成:
根据对称性,可以进一步简化为:
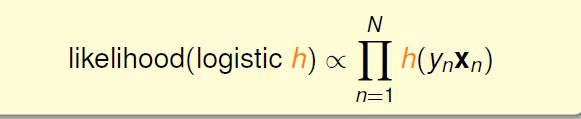
P(x)用灰色是因为对于所有 h 来说 P(x)一样,所以 likelihood(h)正比于 h(yx)连乘:
所以现在就是要求解一个h使得likelihood(h)最大:
因为 h(x)= θ(wT x),所以可以写成:
取 ln 将连乘换成连加:
取负将最大化变为最小化,1/N 是常数,不影响,为了后续计算方便:
进一步变换表达式:
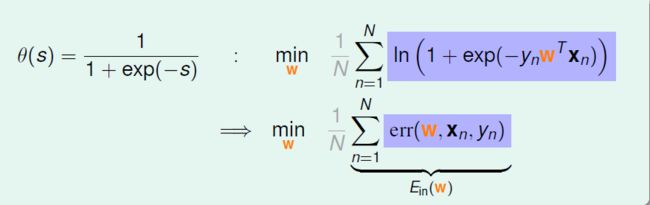
至此,将 err(w,x,y)= ln(1 + exp(-y w x))叫做 Cross-Entropy Error,取平均就得到了 Ein 。
3、Minimize Ein(w)& 迭代优化
得到了Ein(w),下面就是得到一个w使得Ein最小了!
这个Ein(w)是 连续的(continuous)、可微分的differentiable、二次可微(twice-differentiable)、凸函数(convex)。
和LinReg思路一样,找到“谷底”,让Ein的梯度等于0.。所以首先,求出Ein(w)的梯度。过程略,结果为:
让梯度等于0。什么时候等于0?θ(-y w x)= 0的时候。如果θ为0,则需要(y w x)正无限大,也代表 y 和 (w x)同号…这就意味着data需要是线性可分的。如果data不是线性可分的时候,很难得出结果。Ein的梯度是非线性的等式,需要一种新的方法求解:迭代优化。
求解思路可以从PLA中(参看Lec 2)获得启发,PLA是一步一步的修正(LinReg是一步登天)。PLA算法可以用一个等式表示出来:
即遇到错误时就去更新w,正确的话就是加上0。更新部分可以看成两部分:η 和 v。v是更新的方向(向量),η是在更新的方向上走多远。(这个思路后面会常常用到)
类似PLA,选择(η,v)和 终止条件,一轮一轮的优化的方式叫做 iterative optimization 。(重要!!)
4、Gradient Descent
这一节将介绍在LogReg里面用到的一种 迭代优化 方法:梯度下降!(这个方法也很重要,不是只适用于这种情况)
进行迭代优化需要找出方向v,已知Ein是一个convex、continuous的曲线,如图:
要得到最小的Ein(w),可以想象成有一个小球在半山腰,要往谷底走……这里固定v是单位长度的,一次走多大步全由η决定。
如果用贪心的方法(即最快的滚下去),该向什么方向走呢?这里用 泰勒展开(Taylor expansion)将Ein(w)变成一个关于v的线性的式子:
当η够小的时候,上式成立。现在问题就变为:
现在就只剩下确定 v 。v和Ein两个向量相乘,怎么样最小?反向的时候最负。(可以这样想:如果一条直线的k>0,说明直线向右上升,应该向左走,反之,向右走),所以:
这时候,对于small η :
这种方法就是 Gradient Descent,这是一个简单通用的工具!
确定了方向v,η如何确定?什么样的η是好的?看图
从图上可以形象的看出,太大太小都不好,要适中。从第三张图可以看出,坡度大的时候可以跨大步,坡度小的时候跨小步,使用变化的η较好。所以有一种方法,就是取η与坡度大小正相关。梯度大小也可以反映出距离谷底的远近。
带入w的更新式子,可以约掉 || Ein(wt)|| ,注意:紫色的η和红色的η不是同一个η,新的更新式子为:
η 叫做 fixed learning rate 。η 小会学的慢,η大会学的快一点。
现在就可以给出完整的LogReg 算法了:
in practice,终止条件通常取 ≈ 0