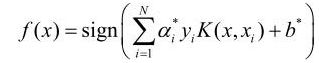1. SVM算法原理
支持向量机(Support Vector Machine)算法需理解清楚三个关键点:间隔,对偶问题,核技巧。
1.1 求解目标
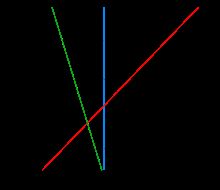
对于线性可分的样本,找到一个超平面使得两个样本距离这个超平面的间隔最大。这样做的目的是为了减小模型的泛化误差(为什么?参见文献6)。如下图中,超平面H3就优于H2,因为两个样本距离超平面H3的间隔更大。
为什么叫支持向量机?下图中超平面H1和H2被称为间隔边界,处在间隔边界上的向量xi被称为支持向量Support Vector。在决定分离超平面时只有SV其作用,移动或去掉其他样本并不会影响分离超平面的位置。因此,支持向量机仅有少量的关键样本确定。
1.2 对偶算法
寻找最大样本间隔的超平面等价于求解最小的几何间隔(即,超平面法向量的L2范数。具体推导过程请见参考文献[4])。将寻找分离超平面的问题构造为以下最优化问题
这是一个带不等式约束条件的问题。可将此问题转化为拉格朗日对偶问题。目的是将约束条件与原始问题放入同一个等式中再进行求解(详情请参考文献[3])。
1.3 软间隔
当样本线性不可分时,引入松弛变量使得函数间隔加上松弛变量大于等于1。于是将学习问题构造为以下规划问题。解此问题而得到的分类决策函数被称为线性支持向量机。线性支持向量机的解w唯一但是b并不唯一。
C>0为惩罚函数,用来调节对误分类的惩罚的大小,视具体问题而定。最小化目标函数必须使目标函数中的两项都尽量小,而C是用来调节两项关系的系数。
1.4 核技巧
核技巧的基本思想就是通过一个非线性变换将输入空间映射到一个特征空间,使得输入空间中的超曲面模型对应特征空间中的一个超平面模型,然后在特征空间中利用线性支持向量机进行求解。在线性支持向量机的对偶问题中,利用核函数K(x,z)替代内积,求解得到的就是非线性支持向量机(参考文献3)。
2. SVM的运用
2.1 分类模型,回归模型
R包"e1071",当y变量为factor时,所产生模型为分类模型,当y变量为连续变量时,所产生模型为回归模型。以下例子来自参考文献7。
## training
# linear kernel
svm.model <- svm(x=data, y=labels, type="C-classification",kernel="linear")
# linear kernel with cost as 42
svm.model <- svm(x=data, y=labels, type="C-classification",kernel="linear", cost="42")
# liner kernel 10-fold cross validation
svm.model <- svm(data, labels, type="C-classification",kernel="linear", cross=10)
# polynomial kernel
svm.model <- svm(x=data, y=labels, type="C-classification",kernel="polynomial", degree="2")
# radial (Gaussian) kernel
svm.model <- svm(x=data, y=labels, type="C-classification",kernel="radial", gamma="0.002")
## validation
predicted <- predict(svm.model, data) # test on training set
sum(predicted != labels) # count differences
table(true=labels, pred=predicted) # confusion matrix
2.2 发现异常值
据文献7描述,SVM可用于发现异常值(outliers),不理解具体机制如何,须进一步学习。
名词对照
间隔:margin
软间隔:soft margin
泛化误差:generalization error
对偶问题:dual problem
核函数: kernel
参考
[1] wiki对SVM的解释
[2] [wiki对拉格朗日对偶的解释](http://en.wikipedia.org/wiki/Duality_(optimization)
[3] 李航,《统计学习方法》
[4] 赫然,支持向量机入门系列
[5] CMU Data Mining课程
[6] SVM入门
[7] 'Classification by Support Vector Machines' by Florian Markowetz
[8] '支持向量机通俗导论(理解SVM的三层境界)‘ by July