观察其变量。
## 'data.frame': 1599 obs. of 13 variables:
## $ X : int 1 2 3 4 5 6 7 8 9 10 ...
## $ fixed.acidity : num 7.4 7.8 7.8 11.2 7.4 7.4 7.9 7.3 7.8 7.5 ...
## $ volatile.acidity : num 0.7 0.88 0.76 0.28 0.7 0.66 0.6 0.65 0.58 0.5 ...
## $ citric.acid : num 0 0 0.04 0.56 0 0 0.06 0 0.02 0.36 ...
## $ residual.sugar : num 1.9 2.6 2.3 1.9 1.9 1.8 1.6 1.2 2 6.1 ...
## $ chlorides : num 0.076 0.098 0.092 0.075 0.076 0.075 0.069 0.065 0.073 0.071 ...
## $ free.sulfur.dioxide : num 11 25 15 17 11 13 15 15 9 17 ...
## $ total.sulfur.dioxide: num 34 67 54 60 34 40 59 21 18 102 ...
## $ density : num 0.998 0.997 0.997 0.998 0.998 ...
## $ pH : num 3.51 3.2 3.26 3.16 3.51 3.51 3.3 3.39 3.36 3.35 ...
## $ sulphates : num 0.56 0.68 0.65 0.58 0.56 0.56 0.46 0.47 0.57 0.8 ...
## $ alcohol : num 9.4 9.8 9.8 9.8 9.4 9.4 9.4 10 9.5 10.5 ...
## $ quality : int 5 5 5 6 5 5 5 7 7 5 ...
## X fixed.acidity volatile.acidity citric.acid
## Min. : 1.0 Min. : 4.60 Min. :0.1200 Min. :0.000
## 1st Qu.: 400.5 1st Qu.: 7.10 1st Qu.:0.3900 1st Qu.:0.090
## Median : 800.0 Median : 7.90 Median :0.5200 Median :0.260
## Mean : 800.0 Mean : 8.32 Mean :0.5278 Mean :0.271
## 3rd Qu.:1199.5 3rd Qu.: 9.20 3rd Qu.:0.6400 3rd Qu.:0.420
## Max. :1599.0 Max. :15.90 Max. :1.5800 Max. :1.000
## residual.sugar chlorides free.sulfur.dioxide
## Min. : 0.900 Min. :0.01200 Min. : 1.00
## 1st Qu.: 1.900 1st Qu.:0.07000 1st Qu.: 7.00
## Median : 2.200 Median :0.07900 Median :14.00
## Mean : 2.539 Mean :0.08747 Mean :15.87
## 3rd Qu.: 2.600 3rd Qu.:0.09000 3rd Qu.:21.00
## Max. :15.500 Max. :0.61100 Max. :72.00
## total.sulfur.dioxide density pH sulphates
## Min. : 6.00 Min. :0.9901 Min. :2.740 Min. :0.3300
## 1st Qu.: 22.00 1st Qu.:0.9956 1st Qu.:3.210 1st Qu.:0.5500
## Median : 38.00 Median :0.9968 Median :3.310 Median :0.6200
## Mean : 46.47 Mean :0.9967 Mean :3.311 Mean :0.6581
## 3rd Qu.: 62.00 3rd Qu.:0.9978 3rd Qu.:3.400 3rd Qu.:0.7300
## Max. :289.00 Max. :1.0037 Max. :4.010 Max. :2.0000
## alcohol quality
## Min. : 8.40 Min. :3.000
## 1st Qu.: 9.50 1st Qu.:5.000
## Median :10.20 Median :6.000
## Mean :10.42 Mean :5.636
## 3rd Qu.:11.10 3rd Qu.:6.000
## Max. :14.90 Max. :8.000
整个数据集有13个变量,1599个观察值。
单变量分析
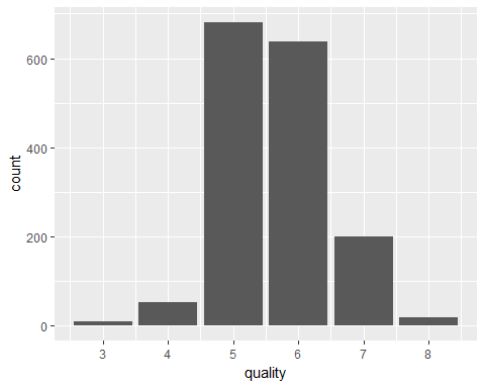
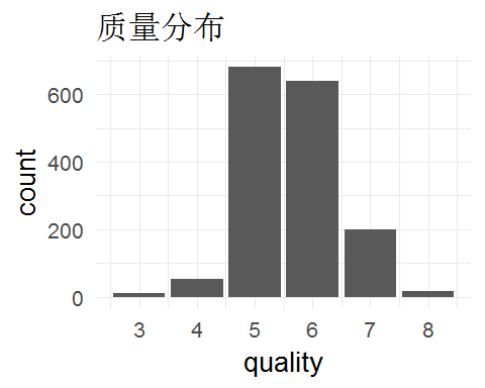
## 3 4 5 6 7 8
## 10 53 681 638 199 18
红葡萄酒分布在最好和最差的比较少,而分布在中间的比较多。
## Min. 1st Qu. Median Mean 3rd Qu. Max.
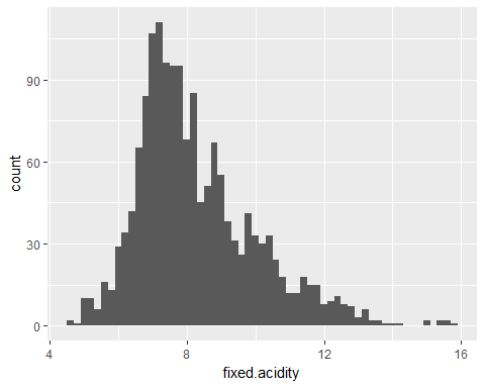
## 4.60 7.10 7.90 8.32 9.20 15.90
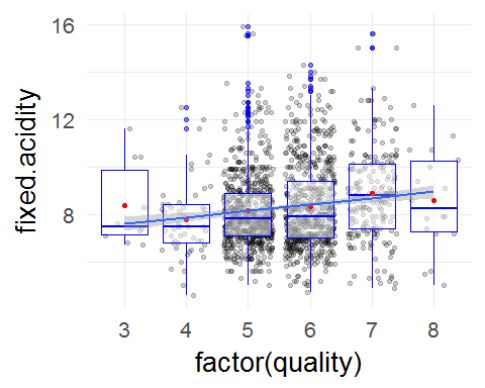
大多数葡萄酒的固定酸度位于7-9(g/dm3)之间。中位数为7.9g/dm3,平均值为8.32g/dm^3。
## Min. 1st Qu. Median Mean 3rd Qu. Max.
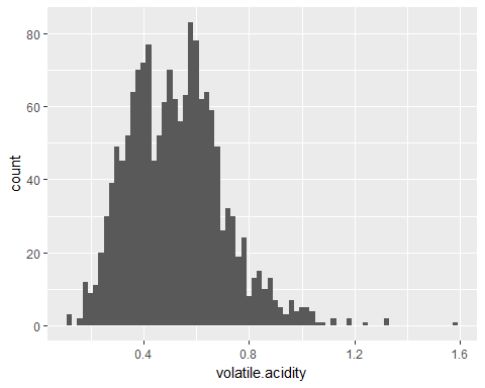
## 0.1200 0.3900 0.5200 0.5278 0.6400 1.5800
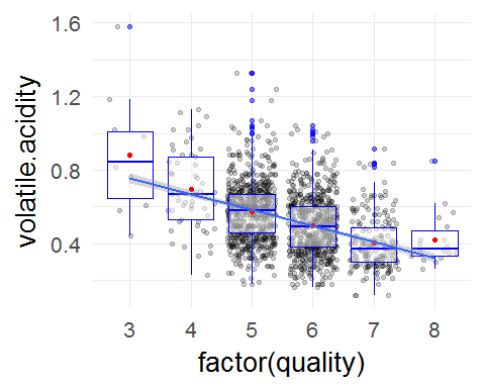
大多数可溶性酸度都位于0.3-1.8(g/dm^3)之间。而从两张直方图中我猜想挥发性酸度可能和可溶性酸度和质量之间可能存在很深的关系。
## Min. 1st Qu. Median Mean 3rd Qu. Max.
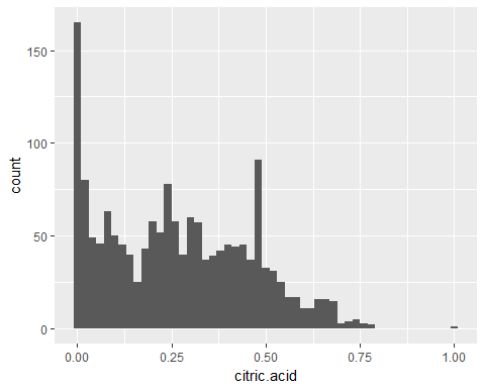
## 0.000 0.090 0.260 0.271 0.420 1.000
##
## 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13 0.14
## 132 33 50 30 29 20 24 22 33 30 35 15 27 18 21
## 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25 0.26 0.27 0.28 0.29
## 19 9 16 22 21 25 33 27 25 51 27 38 20 19 21
## 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37 0.38 0.39 0.4 0.41 0.42 0.43 0.44
## 30 30 32 25 24 13 20 19 14 28 29 16 29 15 23
## 0.45 0.46 0.47 0.48 0.49 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59
## 22 19 18 23 68 20 13 17 14 13 12 8 9 9 8
## 0.6 0.61 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73 0.74
## 9 2 1 10 9 7 14 2 11 4 2 1 1 3 4
## 0.75 0.76 0.78 0.79 1
## 1 3 1 1 1
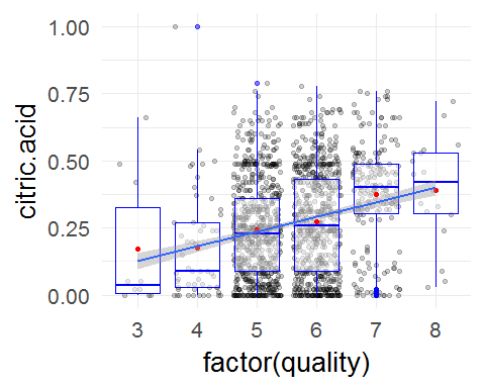
柠檬酸相对于其他两种酸的含量较少,可以看出大多数都处在0-0.5(g/dm^3)之间。
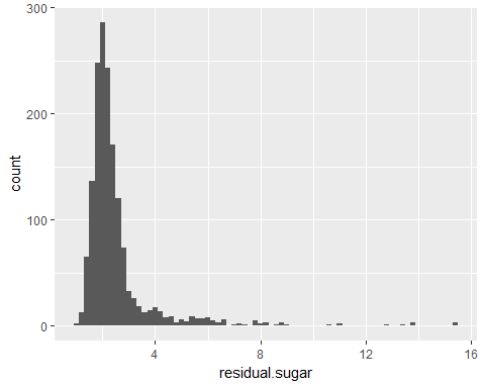
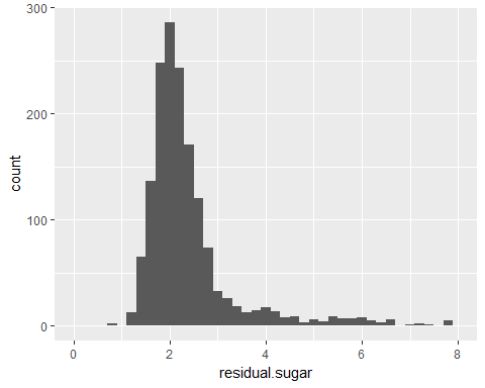
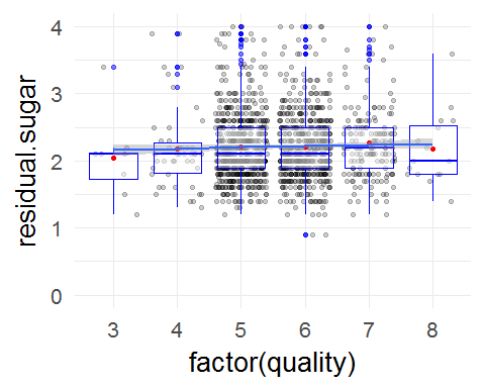
从图中可以看出,糖量有一些异常值,对异常值进行处理,把图像放大。
糖量大部分都在1-4(g/dm^3)之间。
查阅资料中发现,糖酸比是影响评价指标的一个重要因素,糖酸比指总糖和总算的比值。所以我将定义一个新的变量糖酸比。
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.1053 0.2117 0.2482 0.2854 0.3008 2.0807
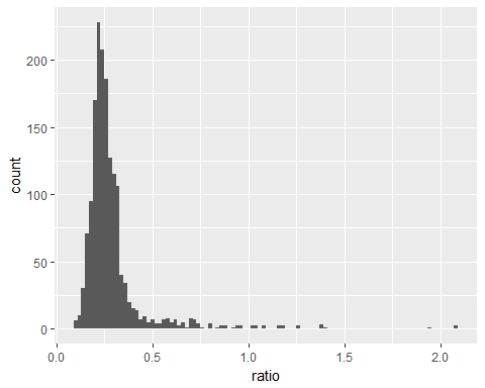
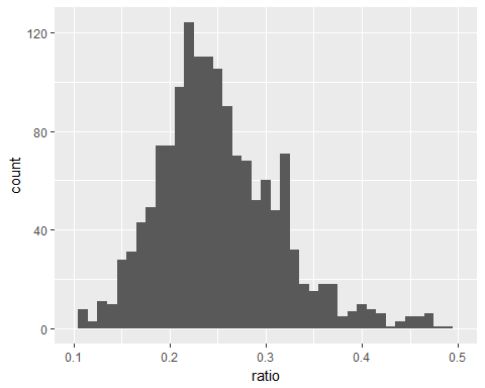
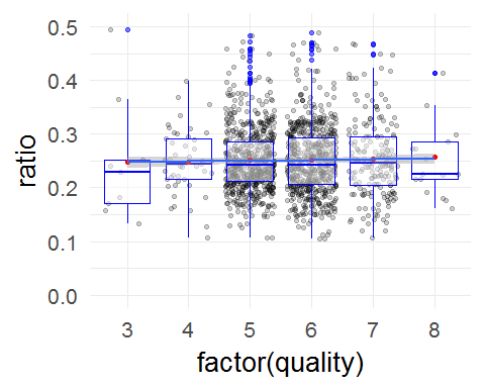
新定义的变量糖酸比(ratio)在绘制直方图时发现存在异常值。将异常值进行处理,将图像放大。
将糖酸比的图放大之后,可以看出糖酸比大多数位于0.2-0.3之间,和质量之间可能存在着联系。
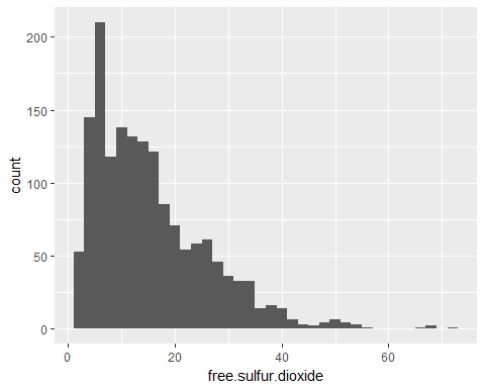
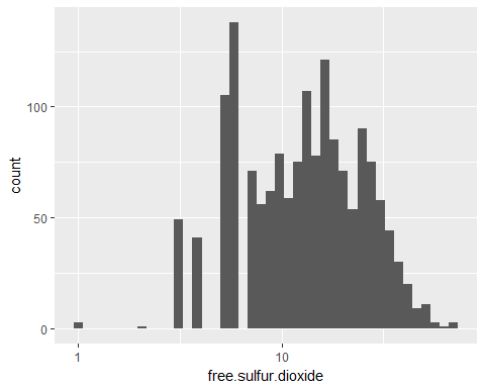
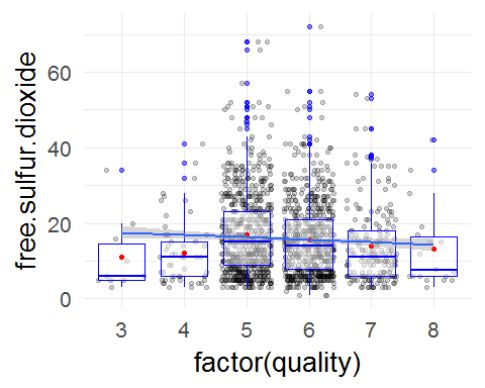
改变长尾数据,游离二氧化硫呈现近似正态分布。
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.00 7.00 14.00 15.87 21.00 72.00
游离二氧化硫大部分值在7-21(mg/dm^3)之间。
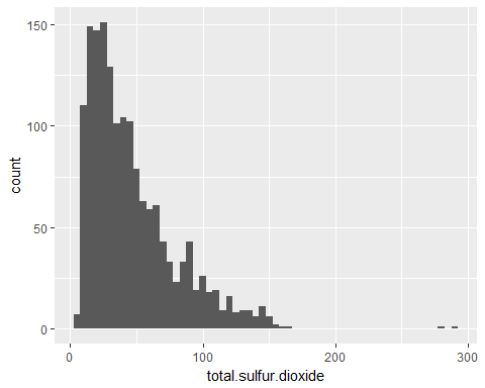
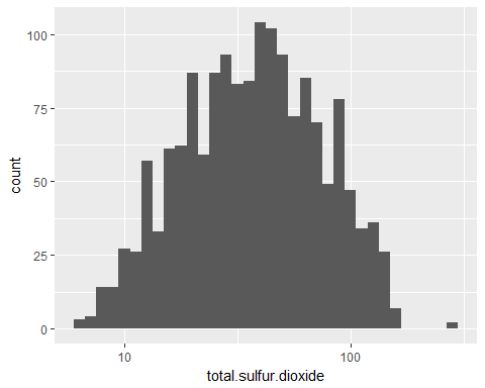
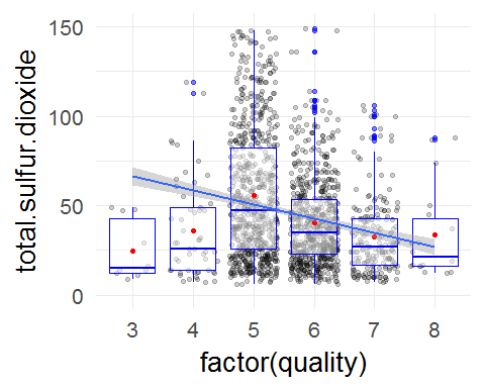
改变长尾数据,总二氧化硫的数量呈现一个比较好的正态分布。
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 6.00 22.00 38.00 46.47 62.00 289.00
总二氧化硫的数量大多在22-70(mg/dm^3)之间。
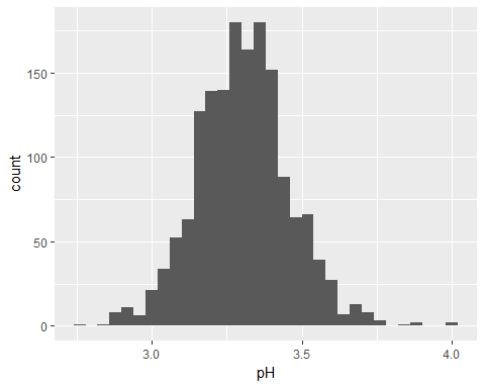
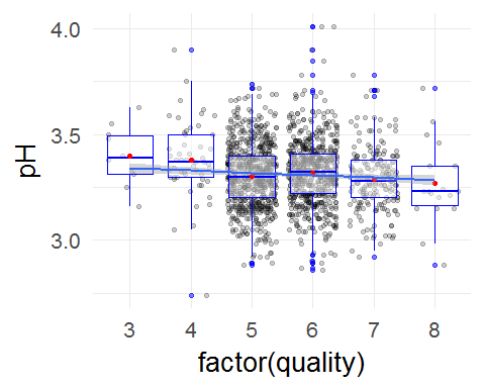
pH值呈现很好的正太分布,大多数都位于3.2-3.5之间。呈现酸性。整个pH值变化不大,而评分是依据味觉来判定的,可能尝不出来酸度的变化。
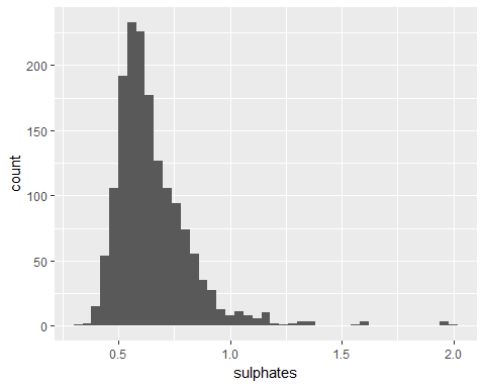
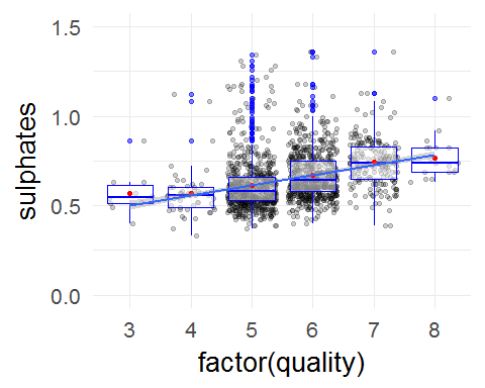
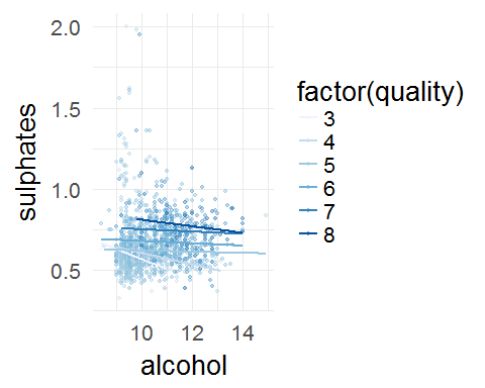
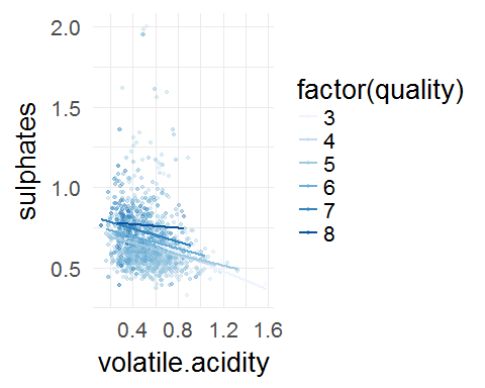
硫酸盐的含量大部分在0.5-0.8(mg/dm^3)之间。 硫酸盐是添加剂,是作为保鲜剂使用的,添加量和其中糖的含量有关系,所以这项指标可能和评分没有直接相关。
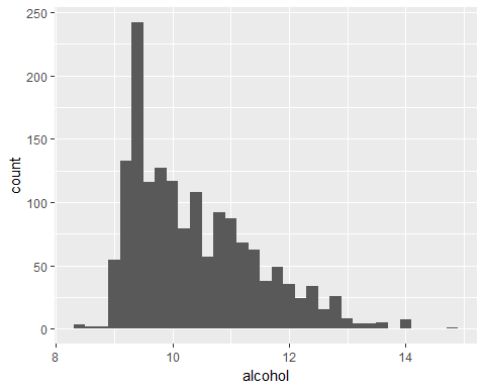
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 8.40 9.50 10.20 10.42 11.10 14.90
酒精含量大多数位于8-12之间,中位数为10.2,平均值为10.42。酒精含量大部分区别不大,但是酒精含量是由葡萄酒发酵程度决定的,所以酒精含量的变化应当和最终的评分有密切的关系。
单变量分析小结
在数据集中有1599种红酒,具有11个特征,即11个输入变量,包括:固定酸度、挥发酸度、柠檬酸、残糖、氯化物、游离二氧化硫、二氧化硫总量、密度、pH、硫酸盐、酒精。以及一个有序因子,即输出变量质量。 其中质量分为3、4、5、6、7、8这几个级别。 其他意见; * 大多数红酒的评级在5、6、7之间。 * 酒精含量的中位数为10.2。 * PH值大多位于3.2-3.5之间。
数据集的主要特征是质量和酒精。可能酒精和其他变量的组合可以更好的预测质量。
在进行糖酸比的绘图的时候,我将其中一部分过大的数据去除了,因为那一部分的糖酸比似乎过大了。 在进行游离二氧化硫和二氧化硫总量的绘图的时候,将长尾数据通过log转换为近似正态分布的数据,是为了更好的看出该数据的特征。
双变量分析
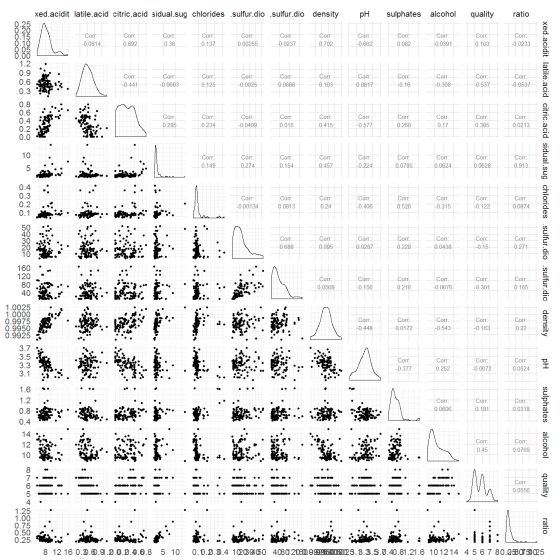
从数据图中可以看出,酒精似乎和质量的相关性较强,而所创建的新变量糖酸比似乎和质量的相关性不高。但是还是想看看这些变量和质量的一些关系。
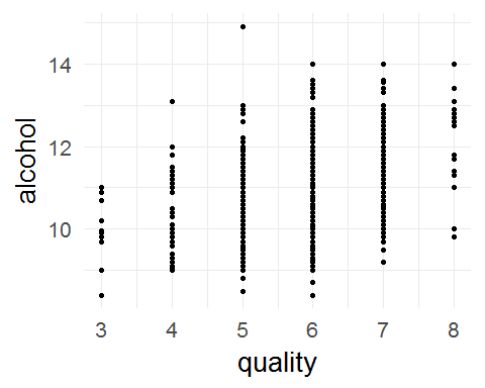
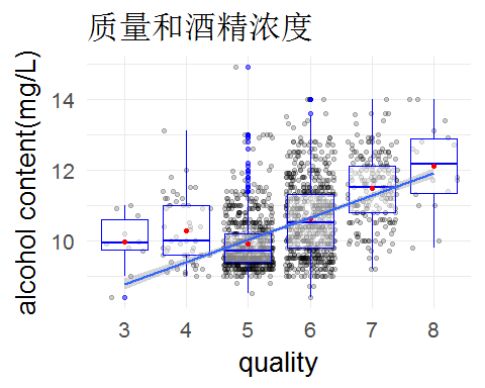
首先先画出质量与酒精浓度的图。
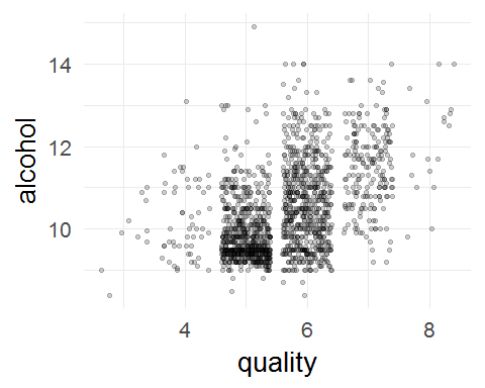
随着酒精浓度的增加,似乎一个酒精浓度能对应很多个质量的酒精,但将其过度绘制后,能看出酒精和质量具有一定的相关性。
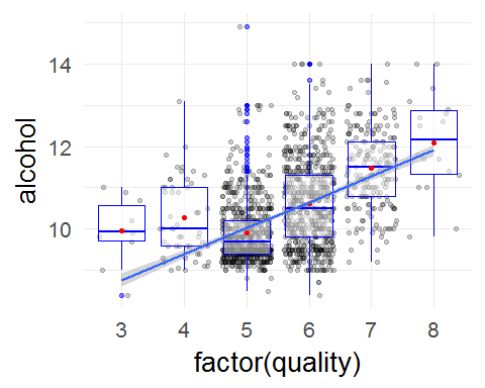
经过散点图的绘制,发现单纯的散点图并不能特别清楚的表现变量之间的关系,而质量又是分等级的,所以将其作为分类变量,进行进一步的处理。
##
## Calls:
## m1: lm(formula = I(quality) ~ I(alcohol), data = wr)
## m2: lm(formula = I(quality) ~ I(ratio), data = wr)
## m3: lm(formula = I(quality) ~ I(free.sulfur.dioxide), data = wr)
## m4: lm(formula = I(quality) ~ I(total.sulfur.dioxide), data = wr)
## m5: lm(formula = I(quality) ~ I(total.sulfur.dioxide), data = wr)
## m6: lm(formula = I(quality) ~ I(pH), data = wr)
##
## =============================================================================================
## m1 m2 m3 m4 m5 m6
## ---------------------------------------------------------------------------------------------
## (Intercept) 1.875*** 5.668*** 5.698*** 5.847*** 5.847*** 6.636***
## (0.175) (0.040) (0.037) (0.034) (0.034) (0.433)
## I(alcohol) 0.361***
## (0.017)
## I(ratio) -0.111
## (0.123)
## I(free.sulfur.dioxide) -0.004*
## (0.002)
## I(total.sulfur.dioxide) -0.005*** -0.005***
## (0.001) (0.001)
## I(pH) -0.302*
## (0.131)
## ---------------------------------------------------------------------------------------------
## R-squared 0.2 0.0 0.0 0.0 0.0 0.0
## adj. R-squared 0.2 -0.0 0.0 0.0 0.0 0.0
## sigma 0.7 0.8 0.8 0.8 0.8 0.8
## F 468.3 0.8 4.1 56.7 56.7 5.3
## p 0.0 0.4 0.0 0.0 0.0 0.0
## Log-likelihood -1721.1 -1926.2 -1924.6 -1898.8 -1898.8 -1924.0
## Deviance 805.9 1041.6 1039.5 1006.5 1006.5 1038.7
## AIC 3448.1 3858.4 3855.2 3803.5 3803.5 3853.9
## BIC 3464.2 3874.6 3871.3 3819.7 3819.7 3870.1
## N 1599 1599 1599 1599 1599 1599
## =============================================================================================
从上述图中可以看出。质量会随着酒精浓度,硫酸盐的添加量以及pH值的变化而变化。其中,在质量为5的时候,不呈现酒精浓度反而下降了,因为这是专家主观测试,而且还存在很多异常值,所以这个下降可以忽略掉。 我通过查阅资料获得的糖酸比这一属性似乎与质量评比没有关系。可能是因为这是专家主观评审,而糖酸比是需要机器测定的,用来客观评价葡萄酒的,所以可能是在这个数据中没有关联的原因。 然而,糖分和酸度应该对口感都有影响,所以,我针对这几个变量在绘制其箱线图,看看他们的关系。
##
## Calls:
## m7: lm(formula = I(quality) ~ I(alcohol), data = wr)
## m8: lm(formula = I(quality) ~ I(volatile.acidity), data = wr)
## m9: lm(formula = I(quality) ~ I(citric.acid), data = wr)
## m10: lm(formula = I(quality) ~ I(residual.sugar), data = wr)
##
## ===================================================================
## m7 m8 m9 m10
## -------------------------------------------------------------------
## (Intercept) 1.875*** 6.566*** 5.382*** 5.616***
## (0.175) (0.058) (0.034) (0.042)
## I(alcohol) 0.361***
## (0.017)
## I(volatile.acidity) -1.761***
## (0.104)
## I(citric.acid) 0.938***
## (0.101)
## I(residual.sugar) 0.008
## (0.014)
## -------------------------------------------------------------------
## R-squared 0.2 0.2 0.1 0.0
## adj. R-squared 0.2 0.2 0.1 -0.0
## sigma 0.7 0.7 0.8 0.8
## F 468.3 287.4 86.3 0.3
## p 0.0 0.0 0.0 0.6
## Log-likelihood -1721.1 -1794.3 -1884.6 -1926.5
## Deviance 805.9 883.2 988.8 1042.0
## AIC 3448.1 3594.6 3775.2 3859.0
## BIC 3464.2 3610.8 3791.3 3875.1
## N 1599 1599 1599 1599
## ===================================================================
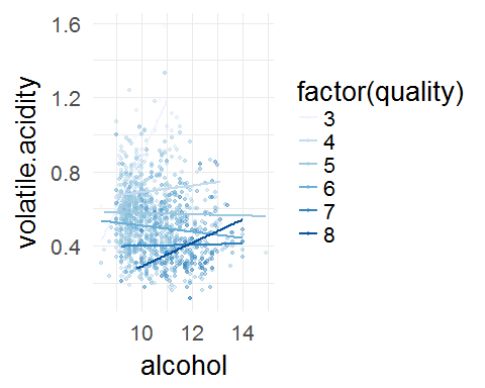
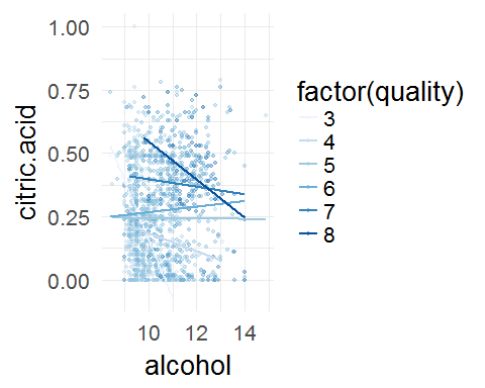
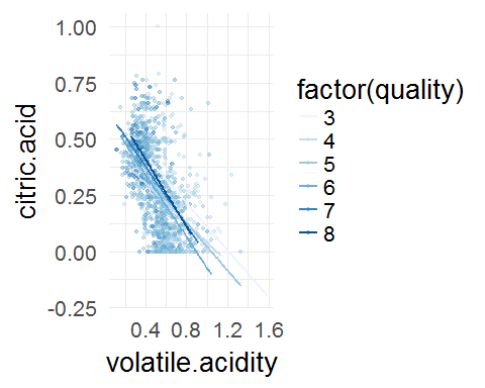
从上述图中可以看出,挥发性酸度与质量呈现比较强的反比关系,似乎是变量之中关系最强的,而柠檬酸与质量呈现正比关系,查阅资料可知,挥发性酸度过高会导致不愉快的醋味,柠檬酸可以增加葡萄酒的新鲜度和风味,这些都是能通过嗅觉及味觉感受出来的,所以可能被作为了专家评分的标准之一。
双变量分析小结
我观察到质量与酒精浓度、硫酸盐的含量以及柠檬酸的含量呈正比关系,而与挥发性酸度及pH值呈反比关系。
其中质量和挥发性酸度有很强的负相关关系,此外,质量与酒精也有比较强的正相关关系。
观察到糖酸比这个属性似乎与质量没有关联。并且糖量这个属性似乎与质量也没有什么关系,可能是含糖量太少,以致尝不出甜味的缘故。
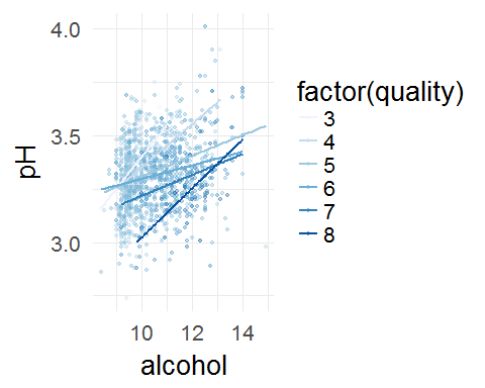
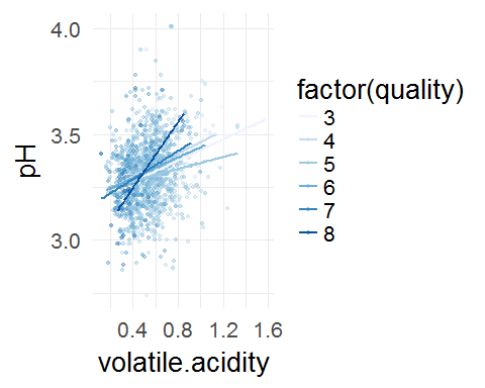
柠檬酸和pH值有较强的反比关系。可能是柠檬酸的酸性较弱,其存在会提高葡萄酒的pH值。
多变量分析
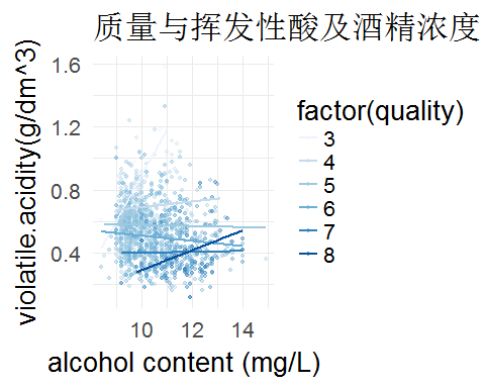
在这张图中,当酒精浓度比较低时,不管挥发性酸如何变化,质量都不高,当挥发性酸比较高时,不管酒精浓度如何变化,质量也不会高。只有在两者都在比较好的区间内,质量才会比较好。
再绘制其他相关特征的图
从以上图可以看出,三个变量之间的关联性不大,在挥发性酸和酒精浓度极高或极低的时候,基本上评分就取决于这两者。在只有在两者都居中时,评分才会收到其他因素的影响。 因此,专家的评分可能是根据以下的线索,如果酒精浓度和挥发性酸出现问题的时候,会直接根据这两个因素给予评分,当这两个因素没有太大问题的时候,就会考虑其他的加分项和减分项。
多变量分析小结
第三个变量的加入对最后的判断似乎影响不大。只有其中的某个值偏大或偏小的时候,评分才会受到这个值的影响。
最终图及总结
图1
大部分评分都在中间的5和6之中,相对较低和较高的评分都比较少,专家评分可能是根据某一项或几项特征特别好或不好来进行加减分的,而大部分酒都没有突出的地方。
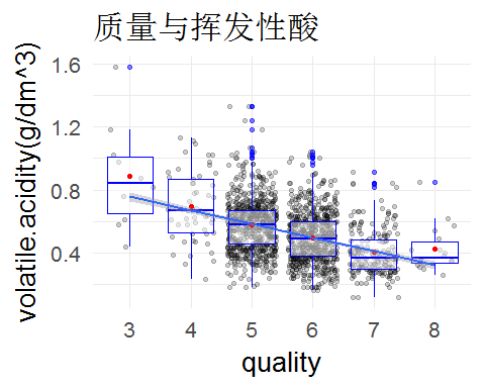
图2
具有较高质量的红酒有较高的酒精浓度或较低的挥发性酸,而低质量的红酒则酒精浓度比较低或挥发性酸比较高。
图3
这张图表示,单一变量的影响远远大于两个变量的共同影响,只有在酒精浓度不低,挥发性酸不高的情况下,质量才会比较不错。因此说明在一个变量出现很大问题的情况下,不管其他变量如何变化,质量都不会有太大的变化,因此专家评分的逻辑可能是这样的,当一个变量很差的时候,不管其他变量如何好,基本上评分不会太高,而只有当其他变量都一般甚至特别好的时候,一个变量特别好才会使评分比较好。
反思总结
红酒数据集包括12个变量,1599瓶红酒的信息。 一开始我进行了每个变量的分析,然后把其中的一些变量和质量放在一起进行分析,最后进行了两个变量和红酒质量的分析,试图寻找其中的相关性。 在一开始我进行单一变量分析的时候,引入了一个新的变量:糖酸比(ratio),但是在进行相关性分析的时候,发现这个变量和最后的评分基本没有相关性可言,我认识到客观评价可能和主观评价的结果有一定区别,所以放弃了这个变量,将构成这个变量的几个变量重新和红酒质量进行相关性分析,找出来与红酒质量相关性比较大的变量:挥发性酸(volatile.acidity)。 在进行双变量分析的过程中,我一开始使用的散点图进行分析,但是没能很好的发现变量之间的相互关系,后来把质量看成一个分类变量,用箱线图进行分析,双变量之间的相互关系就有了一个比较清楚的可以表示出来的图。 在进行多变量之间的关系的时候,发现不管那三个变量,都没有很清晰的关系,后来我考虑到质量是一个主观的评价,所以我做出了大胆的假设:当一个变量很差的时候,不管其他变量如何好,基本上评分不会太高,而只有当其他变量都一般甚至特别好的时候,一个变量特别好才会使评分比较好。并且图中表示的关系也能够证明我的假设。 在分析过程中,对本来很多不太了解的统计学知识比如r2,比如箱线图有了更深一层次的了解。成功的自学了如何在R中创建函数。在研究变量之间相互关系的时候,发现了新创建的变量糖酸比和和糖量的关系非常大,而含糖量和最后的质量评分关系却不大,我猜想这可能和人的味觉有关,人能够清晰地感知酸但是可能对甜要超过一定限度才会清楚的感知到,可能人们感到酸时,酸只有很小的一部分,而感到甜时,糖已经有很多了。这也可能是挥发性酸能很大程度影响最后评分的原因。 对于未来的工作方面,我需要加强统计学方面的学习,对于统计学很多方面知识的不熟悉导致分析过程不太顺利,甚至影响到了最后的结果,所以,统计学等数学知识是我急需补充的。另外,编程的能力也需要大大提高,对于ggplot这个库还需要更多的学习,以便画图时候更加轻松。
参考资料:R for Data Science