灵活&&高效的符号表--二叉查找树

一丶定义

一颗二叉查找树是一颗二叉树，其中每个结点的键都大于其任左子树任意结点的键而小于右子树任意结点的键。如标题所述，它有着链表插入的灵活性和有序数组查找的高效性。

二丶基本实现

注：本文采用的是C++语言实现 但算法与数据结构是一种思想 与语言无关。

1.查找

查找的思路比较简单，需要查找的键存在当前树中就直接返回相应的值，如果查找的键小于根结点就在左子树中继续递归查找，大于就在右子树中查找，最后没查找到就直接返回一个空链接。
相关代码如下

if ( node == NULL) {
     return NULL;
}
if (key == node->key) {
   return &(node->value);
} else if (key < node->key) {
    return search(node->left,key);
} else {
    return search(node->right,key);
}

2.插入

插入的思路与查找差不多，插入时树如果为空，就返回含有一个该键值对的新结点。如果被查找的键小于根结点的键就继续在左子树中插入该键，大于则往右子树插入。代码如下

if (node == NULL) {
      count++;
      return new Node(key,value);
 }
if (key == node->key) {
   node->value = value;
} else if(key < node->key) {
   node->left = insert(node->left,key,value);
} else if (key > node->key) {
   node->right = insert(node->right,key,value);
}

return node;

3.删除操作

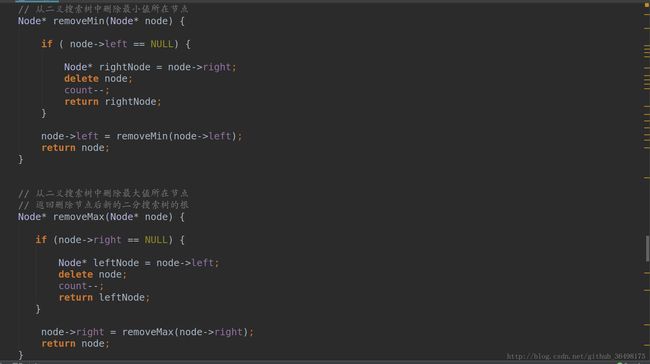
首先简单介绍下删除最大与最小结点。直接分别递归在左丶右子树中找到最小与最大的结点，删除后返回新的二叉树所对应的根结点。
如下图所示

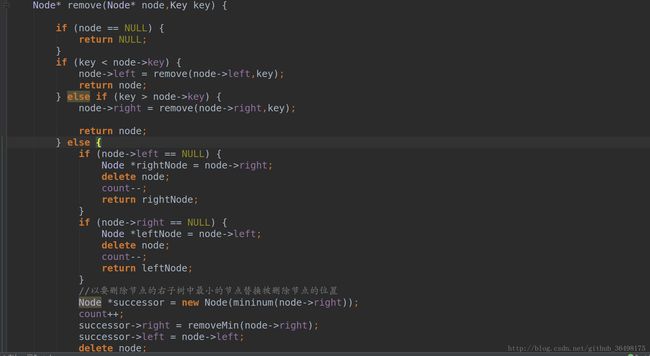
这里重点介绍下删除任意结点的操作。因为我们在进行删除操作时必须还有保持二叉查找树的有序性。所以删除当前结点后还要进行适当的操作，有2种选择: 第一种方法是取当前结点（也就是被删除的结点）的右子树中的最小结点替换被删除结点的位置，第二种方法是取当前结点的左子树中的最大结点替换被删除结点的位置。注意在这个过程我们需要用到查找最小与最大结点的函数 其实看了前面的查找插入后这个实现是很简单的 后面会给出代码。然后所取结点的左端与右端分别连接到被删除结点的左右端，同理删除之前先要判断结点是否为空，以及不为空时的位置。如下图(暂时只有第一种情况 不过思路一样 后面会给出）

看看上面的删除最大或者最小结点时 返回的是当前结点。所以这里的successor的右结点就直接指向这个方法的返回值。每次删除与替换时要注意递减与递增操作。

4.遍历

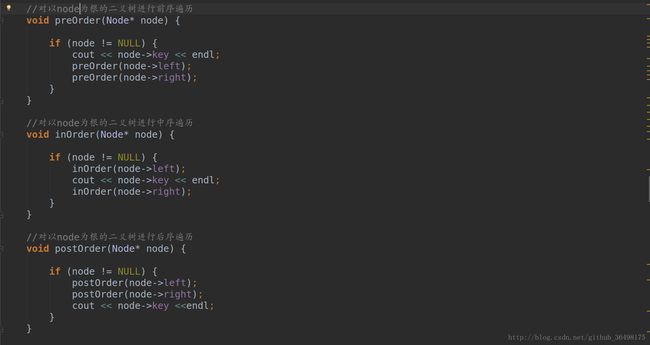
二叉树叉遍历分为前序丶后序丶中序遍历以及层序遍历。
前序遍历：先遍历当前结点→然后遍历左子树→最后遍历右子树 。
中序遍历：先遍历左子树→然后遍历当前结点→最后遍历右子树。
后序遍历：先遍历左子树→然后遍历右子树→最后遍历当前结点。
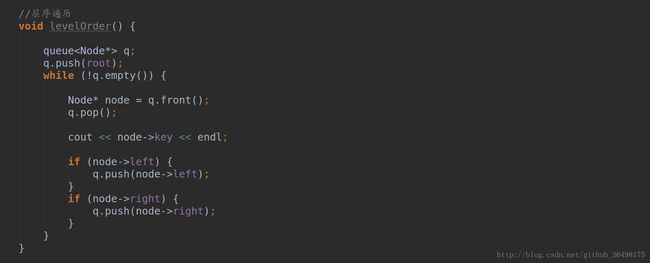
层序遍历：也称广度优先遍历，从根结点开始在每层从左至右进行遍历。
具体就是直接按顺序递归

上面三种遍历的实现没什么区别，这里重点介绍下层序遍历。这里可以创建一个队列，然后把根结点push进去，再用一个循环，得到一个队首的元素，pop出队列，并判断是当前结点是否有左右孩子，有就push进队列，然后继续循环直到队列为空。如下所示

5.向上与向下取整操作

向上取整(floor):查找小于当前结点的最大值。如果给定的键与根结点的键相等，那么根结点本身就是floor结点。如果给定的键小于根结点的键，那么floor结点一定位于根结点的左子树中；如果给定的键大于根结点的键，那么根结点可能就是floor结点，也可能不是，所以要继续在根结点的右子树中递归查找。代码如下图

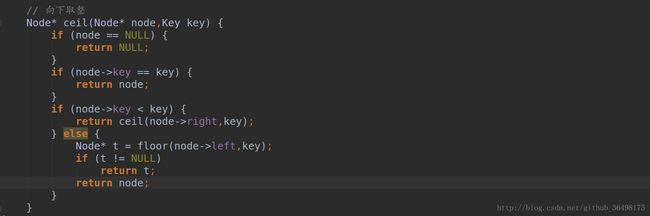
向下取整(ceil):查找大于当前结点的最小值。同样，如果给定的键与根结点相等，那么根结点本身就是ceil结点。如果给定的键大于根结点的键，那么ceil结点一定位于根结点的右子树中；如果给定的键小于根结点的键，那么根结点可能就是ceil结点，也可能不是，所以要继续在根结点的左子树中递归查找。代码如下图

6.选择与排名

选择（select）：现在我们要查找排名为k的键，如果左子树中的结点数count大于k，就继续递归的在左子树中查找排名为k的键；如果k等于count，就直接返回当前结点；如果count小于k，就继续递归的在右子树中查找排名为k-count-1的键。
代码如下图

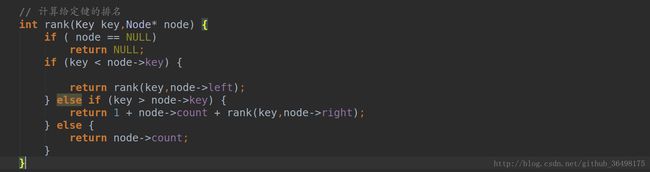
排名（rank）：rank()是select()的逆过程，它返回给定键的排名。如果给定的键和根结点的键相等，则返回根结点的左子树中结点的总数。如果给定的键小于根结点，就递归的计算该结点在左子树的排名；如果给定的键大于根结点，就返回根点的数量加上它在右子树中的排名(递归计算）。
代码如下图

这里写图片描述

三丶总结

总的来说，二叉树的实现并不困难，且当树的构造和随机模型近似时在各种实际应用场景它都能进行快速的查找和插入，它高效的解决了很多在之前看似不可能的任务，本文也只是介绍了一些常用的，更多实现可以自己去搜索。不过二叉查找树也有自己的缺点，它在最坏情况下（也就是树的所有操作都沿着一条或两条路径进行）所需的时间和树的高度成正比。于是为了解决问题就出现了后来的平衡二叉树和红黑树，这里就不多说了。最后附上二叉查找树的全部代码，代码虽然有点长，但是每一部分理解了整体理解就不难了。

template 
class BST {

private:
    struct Node {
        Key key;
        Value value;
        Node *left;
        Node *right;
        int count;

        Node(Key key,Value value,int count) {
            this->key = key;
            this->value = value;
            this->left = this->right = NULL;
            this->count = count = 0;
        }

        Node(Node *node) {
            this->key = key;
            this->value = value;
            this->left = node->left;
            this->right = node->right;
        }
    };

    Node *root;
    int *count;

public:
    BST() {
        root = NULL;
        count = 0;
    }
    ~BST() {
        destroy(root);
    }

    int size() {
        return *count;
    }

    bool isEmpty() {
        return count == 0;
    }

    void insert(Key key,Value value) {

        root = insert(root,key,value);
    }

    bool contain(Key key) {

        return contain(root,key);
    }

    Value* search(Node* node,Key key) {

        if ( node == NULL) {
            return NULL;
        }

        if (key == node->key) {
            return &(node->value);
        } else if (key < node->key) {
            return search(node->left,key);
        } else {
            return search(node->right,key);
        }

    }

    //前序遍历
    void preOrder() {
        preOrder(root);
    }

    //中序遍历
    void inOrder() {
        inOrder(root);
    }

    //后序遍历
    void postOrder() {
        postOrder(root);
    }

    //层序遍历
    void levelOrder() {

        queue q;
        q.push(root);
        while (!q.empty()) {

            Node* node = q.front();
            q.pop();

            cout << node->key << endl;

            if (node->left) {
                q.push(node->left);
            }
            if (node->right) {
                q.push(node->right);
            }
        }
    }

    // 寻找最小的键值
    Key mininum() {

        assert( count!= 0);
        Node* minNode = mininum(root);

        return minNode->key;
    }

    // 寻找最大的键值
    Key maxnum() {

        assert( count != 0);
        Node* maxNode = maxnum(root);
        return maxNode->key;
    }

    // 从二叉树中删除最小值所在节点
    void removeMin() {

        if (root) {
            root = removeMin(root);
        }
    }

    // 从二叉搜索树中删除最小值所在节点
    void removeMax() {

        if (root) {
            root = removeMax(root);
        }
    }

    // 从二叉搜索树中删除键值为key的节点
    void remove(Key key) {

        root = remove(root,key);
    }

    // 获取小于当前结点的最大结点
    Key* floor(Key key) {

        if ( count == 0 || key < mininum()) {
            return NULL;
        }

        Node *floorNode = floor(root,key);
        return &(floorNode->key);
    }

    // 获取大于当前结点的最小结点
    Key* ceiling(Key key) {

        if ( count == 0 || key > maxnum())
            return NULL;

        Node *ceilNode = ceil(root,key);
        return &(ceilNode->key);

    }

    // select操作
    Key* select(int k) {
        return select(root,k)->key;
    }

    // rank操作
    Key* rank(Key key) {
        return rank(key,root);
    }

private:
    // 向以node为根的二叉搜索树中 插入节点(key,value)
    // 返回插入新节点后的二叉树的根
    Node* insert(Node *node,Key key,Value value) {

        if (node == NULL) {
            count++;
            return new Node(key,value,count);
        }

        if (key == node->key) {
            node->value = value;
        } else if(key < node->key) {
            node->left = insert(node->left,key,value);
        } else if (key > node->key) {
            node->right = insert(node->right,key,value);
        }

        return node;
    }

    // 查看以node为根的二叉搜索树中是否包含键值为key的节点
    bool contain(Node* node,Key key) {

        if ( node == NULL) {
            return false;
        }

        if (key == node->key) {
            return true;
        } else if(key < node->key){
            return contain(node->left,key);
        } else {
            return contain(node->right,key);
        }
    }


    //对以node为根的二叉树进行前序遍历
    void preOrder(Node* node) {

        if (node != NULL) {
            cout << node->key << endl;
            preOrder(node->left);
            preOrder(node->right);
        }
    }

    //对以node为根的二叉树进行中序遍历
    void inOrder(Node* node) {

        if (node != NULL) {
            inOrder(node->left);
            cout << node->key << endl;
            inOrder(node->right);
        }
    }

    //对以node为根的二叉树进行后序遍历
    void postOrder(Node* node) {

        if (node != NULL) {
            postOrder(node->left);
            postOrder(node->right);
            cout << node->key <left);
            destroy(node->right);

            delete node;
            count--;
        }
    }

    // 寻找最小的键值对应的节点
    Node* mininum(Node* node) {

        if (node->left == NULL) {
            return node;
        }
        return mininum(node->left);
    }

    // 寻找最大的键值对应的节点
    Node* maxnum(Node* node) {

        if (node->right == NULL) {
            return node;
        }
        return maxnum(node->right);
    }

    // 从二叉搜索树中删除最小值所在节点
    Node* removeMin(Node* node) {

        if ( node->left == NULL) {

            Node* rightNode = node->right;
            delete node;
            count--;
            return rightNode;
        }

        node->left = removeMin(node->left);
        return node;
    }


    // 从二叉搜索树中删除最大值所在节点
    // 返回删除节点后新的二分搜索树的根
    Node* removeMax(Node* node) {

       if (node->right == NULL) {

           Node* leftNode = node->left;
           delete node;
           count--;
           return leftNode;
       }

        node->right = removeMax(node->right);
        return node;
    }

    // 删除以node为根的二分搜索树中键值为key的节点
    // 返回删除节点后新的二分搜索树的根
    Node* remove(Node* node,Key key) {

        if (node == NULL) {
            return NULL;
        }

        if (key < node->key) {
            node->left = remove(node->left,key);
            return node;
        } else if (key > node->key) {
            node->right = remove(node->right,key);

            return node;
        } else {

            if (node->left == NULL) {
                Node *rightNode = node->right;
                delete node;
                count--;
                return rightNode;
            }
            if (node->right == NULL) {
                Node *leftNode = node->left;
                delete node;
                count--;
                return leftNode;
            }
            //以要删除节点的右子树中最小的节点替换被删除节点的位置
            Node *successor = new Node(mininum(node->right));
            count++;

            successor->right = removeMin(node->right);
            successor->left = node->left;

            delete node;
            count--;
            return successor;
        }
    }

    // the second remove
    Node* remove2(Node* node,Key key) {

        if (node == NULL) {
            return NULL;
        }

        if (key < node->key) {
            node->left = remove(node->left,key);
        } else if (key > node->key) {
            node->right = remove(node->right,key);
        } else {
            if (node->left == NULL) {
                Node *rightNode = node->right;
                delete node;
                count--;
                return rightNode;
            }
            if (node->right == NULL) {
                Node *leftNode = node->left;
                delete node;
                count--;
                return leftNode;
            }

            //以要删除的节点的左子树中最大的节点替换被删除节点的位置
            Node* successor = new Node(maxnum(node->left));
            count++;

            successor->left = remove2(node->left,key);
            successor->right = node->right;

            delete node;
            count--;

            return successor;
        }


    }

    // 向上取整
    Node* floor(Node* node,Key key) {
        if (node ==NULL) {
             return NULL;
        }
        if (node->key == key) {
            return node;
        }
        if (node->key > key) {
            return floor(node->left,key);
        } else {
            Node* t = floor(node->right,key);
            if (t != NULL)
                return t;
            return node;
        }
    }

    // 向下取整
    Node* ceil(Node* node,Key key) {
        if (node == NULL) {
            return NULL;
        }
        if (node->key == key) {
            return node;
        }
        if (node->key < key) {
            return ceil(node->right,key);
        } else {
            Node* t = floor(node->left,key);
            if (t != NULL)
                return t;
            return node;
        }
    }

    // 查找排名为k的键
    Node* select(Node* node,int k) {
        if ( node == NULL)
            return NULL;
        int n = node->count; //当前的结点总数
        if (n > k)
            return select(node->left,k);
        else if (n < k)
            return select(node->right,k-n-1);
        else
            return node;
    }

    // 计算给定键的排名
    int rank(Key key,Node* node) {
        if ( node == NULL)
            return NULL;
        if (key < node->key) {

            return rank(key,node->left);
        } else if (key > node->key) {
            return 1 + node->count + rank(key,node->right);
        } else {
            return node->count;
        }
    }
};

参考《c++算法与数据结构》和 《算法第4版》。