题记:昨天2016经济学诺奖揭晓,我正好读完了《合适:从升学择校、相亲配对、拍照拍卖了解新兴实用经济学》。巧的是,这也是一本与诺贝尔经济学有关的小书。科学家用人人能懂的算法,解决实实在在的问题,而本书的作者强悍的是用深入浅出的表达将一个诺奖理论讲的清楚明白,让我收获了破解谜题的阅读快感。其中令人惊叹的TTC算法,连小学生都可以很快学会,但是它又能解决经济学领域的疑难问题。这种反差令人震撼,但这又是切切实实的科学!本文比较长,但是如果你稍微耐心一点,我想你会和我一样深刻感受到经济学思维的层次感和创造性!
——————————————————————————————————
最近,关于房价的问题,最近大热。接下来要讨论的事情确实和房子有点关系,这是一个关于换房子的故事。而这次事关诺贝尔经济学奖得主的换房子故事竟然还意外救了很多人的命!
2012年的诺贝尔经济学奖获得者研究的理论里有这样一个案例,说学校给七个学生每人分到1间房当宿舍,但是这7个人觉得别人的房子比自己的好。所以有人就提议说,要不大家互相换换,没准可以换到比现在更满意的房子。
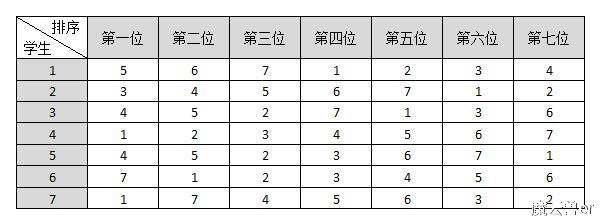
其中有一个人特别善于图形化思考,就提议说咱们列个表吧。为了简化问题,每个学生所在房间以该学生的名字命名。也就是说,现在学生1-7分别住的房间号也叫1-7,就是说学生1住房间1,学生2住房间2,依此类推,一直到学生7住房间7。这些学生对现在的房间不满意。他们对7间房都有自己的偏好,所以呢根据这个就列了下面这张表:
这个表我们可以一目了然地清楚每个人最喜欢哪间房,这样好方便调换。我们来看一下,对于学生1来说,最好的房间是5,其次是6、7、1、2、3、4。这就是学生1的偏好,7个学生的偏好,我们在表格上都可以看到。所以现在我们要做的事情就是参考这个偏好,然后互换一下房间,然后使得“所有人都不会换到比现在更不满意的房间”就行了。
这个问题非常简单对不对,我们随便都可以找到更换的组合,比如:
学生1住房间6,这比他现在住的房间1他要更喜欢一些。学生2住房间 5,学生3住房间2,学生4换到房间3,都比原来满意了。根据上表我们可以看到最满意的就是学生5、6、7了,它们分到了最喜欢的房子。
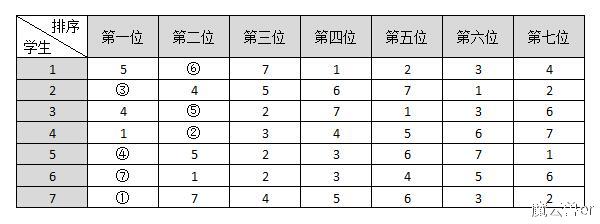
好了,到这一步看来皆大欢喜了。不过其中有一个学生2啊,盯着上面这个分配方案很久,他说不太同意这样分,原来他觉得除了学生1、5、6、7以外,学生2、3、4还可以继续调换,于是在他的提议下,它们达成了这样的协议:
这个学生2果然够聪明,这样一分,每个人几乎都达到了较好的目的。
【表3】这个方案明显是比【表2】好很多,用《合适:从升学择校、相亲配对、拍照拍卖了解新兴实用经济学》里的讲法,【表3】这种分配是对【表2】的帕累托改进。
如果某个分配会被别的分配帕累托改进,就说明在不会使得任何人处境变差的情况下,还有余地让某个人的情况变好,那我们何乐而不为呢。既然资源没有处在最优分配状态,就说明没有得到很好的利用,那我们就有必要进行帕累托改进。直到没办法改进,然后就达到所谓的帕累托最优了。
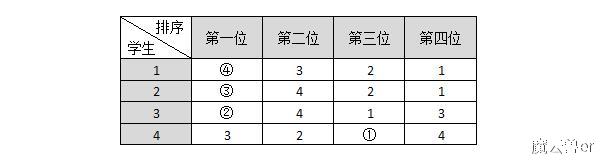
但是帕累托最优的分配大多数时候并不是唯一的。为了讲明白这个问题,我们看一个更简单的情况,比如说4个人分房子,他们各自的偏好如下表:
我们可以用A方案:学生1住房间3,学生2住房间4,学生3住房间1,学生4住房间2。
上面这个其实是有改进空间的,学生1和2对调一下,立刻在不损害其他人的情况下变好了。
这个方案B我们再也无法优化了,这就是帕累托最优,但是帕累托最优解并不是唯一的,假如我们一开始按照方案C来分配:学生1住房间4,学生2住房间3,学生3住房间2,学生4住房间1。具体如下图:
这种情况下,我们发现确实也无法进一步改进了,所以上面这个也算是帕累托最优。
那么问题来了,这样一来我们应该选择哪个方案呢?是方案B还是方案C呢?
在现实生活中会出现这样的情境,即当我们决定用方案B的时候,学生2得到了房间3,学生3得到了房间1,但是这两个学生一看,咦,咱俩对调一下不就行了么,各自都能分到自己满意的,管其他人干嘛?
这样一来,2和3满意了,可是对1和4来讲就不公平了。因为方案B引发了小集团的私下协议。用《合适》的话来讲,发生了“阻止”。如果在分配的时候禁止有这种小集团协议,那么2和3就不会参加换房间了。这样一来可以换的数量减少,更优质的分配就少了。所以我们需要找一个不会发生阻止的分配才行,那么这个在《合适》里叫做强核配置。
这个强核配置有令人震惊的属性,任何分配肯定有解,并且无论分配数量有多大,都仅有一个解!这个结论前半句由沙普利和斯卡夫在1974年论文中证明,后半句由罗斯和安德鲁•波斯尔迪韦特在《数理经济学》证明。
好了,言归正传,说这么多我们还是回到开始的7个人分房子的问题上。我们最终找到了【表3】这么一个分配法:
但是当我们决定按照这个分配的时候,学生1、4、5勾搭上了,说我们内部换了,不跟你们玩了:学生1选了房间5,学生4选了房间1,学生5选了房间4,他们3个皆大欢喜,不管别人了。
这怎么了呢,用我们刚4个人分房子的术语来看,这叫发生了“阻止”,说明这个分配并不是一个强核配置。就是说看起来这个方法不错,但是当你执行的时候,你容易被小集团搞破坏,所以为了防止这种小集团结盟,我们需要找到传说中的强核配置!
可是7个人分房子,分配方式有7!种,7的阶乘有5040种,那怎么才能找到强核配置呢?一个获得过冯诺依曼奖的叫戴维•盖尔的家伙巧妙地解决了这个问题,他发明了一种简单到让人不能相信的算法成功搞定了它,这个算法就是TTC算法。《合适》的作者留学美国的时候,用拙劣的英语就可以和50多岁的大妈讲清楚。
我们还是按照7个人的偏好表来看。TTC算法是这样解决问题的:
〇第一轮
每个学生用手指出对自己来说排在首位的房间,这里“用手指”用箭头来表示:
1→5
2→3
3→4
4→1
5→4
6→7
7→1
以上,1→5就是表示学生1指向了房间5,上面这组组合我们很容易就发现了一个闭环:
1→5→4→1
首尾相连箭头指向想要的东西。因此按照这个分配,我们给学生1分配房间5,给学生5分配房间4,给学生4分配房间1。这样学生1、4、5房间确定,他们离开了。
〇第二轮
现在剩下学生2、3、6、7,他们从剩下的房子中指出了自己最满意的:
2→3
3→2
6→7
7→7
用箭头联结起来的循环我们发现了俩:
2→3→2
7→7
和上一轮一样,分给学生2房间3,分给学生3房间2,然后房间7就分给学生7。
〇第三轮
现在只剩下学生6了,而房间也仅剩下6,所以用箭头表示就是:
6→6
这本身是一个循环,给学生6分配房间6,这个分配就结束了。
而且这个算法牛逼的是,即便有N个学生,最多经过N轮就可以结束,如果用穷举法你需要N的阶乘种!
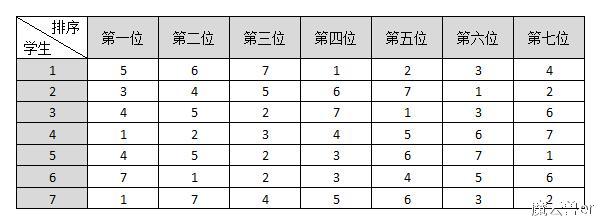
最后我们得到的结果是这样的:
这个看起来很不起眼的分配,正是TTC算法找出来的强核配置!
很多人可能会觉得,这个有前面那个学生2想出来的好吗?确实强核配置里有一个倒霉的学生6,而前面那个配置看起来大家满意度会比较高。但这里的问题并不是满意度,而是要保证公平性,保证不会有小团体,不会发生“阻止”。只有这个唯一解是既满足帕累托最优,又不发生阻止的解,而找到这个解最快的方法就是TTC算法!
更完美的是,这个TTC算法,还满足防策略性,什么意思呢,就是假如你是7个人中的一个,你发现某个房间人气很高,那么你干脆虚报一个没准能搅乱这种分配,听起来这个主意好像很聪明,但事实上罗斯已经证明有这个算法在,那么结果就不会被这种策略性影响!《合适》一书的第31页到第33页,有一个小小的举例,有兴趣的可以看看。1994年发表在《国际博弈论》上的论文还证明强核规则是能满足防策略性、帕累托最优和个体合理性规则的唯一规则!
我们上面讲的这个分房子的例子,其实是沙普利和斯卡夫1974年在《数理经济学》上发表的论文里的精髓。看上去在数学上很完备,也很有趣,不仔细看还给人一种不明觉厉的感觉,可是这东西有啥用处呢,换房子这种事情又不是总能遇得到。
不过呢学术上有很多研究初看时没卵用,但有心人眼里,这些都是解决问题的大工具!很快,就有科学家对这个模型产生了兴趣,他们对这个话题进行了补充和扩展,在“房间-住户”的二元模型中加入了“空房间”“新的入住者”元素,这样一来就产生了奇妙的对应。2004年罗斯、森梅兹和云韦尔在《经济学季刊》上发表了《肾脏交换》的论文。论文的核心就是把住宅分配问题和肾脏移植匹配结合了起来:
♦住户=患者
♦住户的房间=针对某个特定患者的捐献者
♦空房间=捐肾
♦新的入住者=没有捐献者的患者
他们用这个方法,找到了一种解决肾脏移植匹配的办法。众所周知,几乎所有国家都禁止器官买卖,所以无法按照经济学教科书说的那样,用市场来解决供需关系。但是人们虽然排斥器官买卖,可是很多人可以接受患者和捐献者交换。在实际的情况中,经常存在患者和捐献者不适合的情况,那么在肾源作为一种超级紧缺资源的情况下,通过建立不合适组的数据库,做交换配对,反而可以达到资源的有效分配。而我们文章中提到的办法,正好可以用在这个领域。事实上,《合适》就提到了韩国和美国都有这样的数据库。
一个对分房子问题的研究,最后却使得很多肾脏病人受惠,这本身有一种很奇异的美感!当我读这本《合适》的时候,我被经济学家那种富于层次感和创造力的思维逻辑给征服了。我们这篇只是涉及了该书的1/3内容还不到。这本书的后半部分更加精彩,基于匹配理论,作者深入浅出地介绍了择校、相亲、拍卖等更多情况,最后引到了市场设计的探讨上。读完让人击节赞叹!要知道这套理论不仅仅挽救了很多肾衰竭患者,还改善了很多升学择校制度,光拍卖这个课题,就为美国政府带来了高达780亿美元的拍照拍卖收益,2012年诺贝尔经济学奖奖励的也是市场设计这个话题!!
这个日本作者坂井丰贵也十分厉害,能深入浅出地把这个诺贝尔经济学奖的理论用通俗的语言讲的清楚明白,太羡慕这种人了!今天正值2016诺贝尔经济学奖产生,所以最后再次五星级强推这本《合适》!