【维基解密 宇宙 字 (第2018—5—12号 )震惊级绝密文件】
第一题:
有3个人去投宿,一晚30元.三个人每人掏了10元凑够30元交给了老板.
后来老板说今天优惠只要25元就够了,拿出5元命令服务生退还给他们,
服务生偷偷藏起了2元,然后,把剩下的3元钱分给了那三个人,
每人分到1元.
这样,一开始每人掏了10元,
现在又退回1元,
也就是10-1=9,
每人只花了9元钱,
3个人每人9元,
3 X 9 = 27元 + 服务生藏起的2元=29元,
还有一元钱去了哪里?
此题在新西兰面试的时候曾引起巨大反响.
【答案】
三人每人付10元: 老板收25元,服务员藏2元,退回每人1元共3元;
算式: 10X3=25+2+3
最后每人实际付9元共27元。
算式:9X3=27
25+2=27
即服务员藏2元加上老板收的25元等于三人共付的27元。
题中27+2=29是没有数学逻辑依据的,属于误导思维。从而测出你是否有主观的思维能力不被人误导。
第二题:
有个人去买葱问葱多少钱一斤?卖葱的人说 1块钱1斤 这是100斤 要完100元
买葱的人又问 葱白跟葱绿分开卖不
卖葱的人说 卖 葱白7毛 葱绿3毛
买葱的人都买下了
称了称葱白50斤 葱绿50斤
最后一算葱白50×0.7等于35元
葱绿50×0.3等于15元
35+15等于50元
买葱的人给了卖葱的人50元就走了
而卖葱的人却纳闷了
为什么明明要卖100元的葱
而那个买葱的人为什么50元就买走了呢?
【答案】
卖菜的把葱价 分解为葱白价和葱绿价的错误,须知 1斤葱=0.5斤葱白+0.5斤葱绿。那么 1斤葱白价+1斤葱绿价=2斤葱价 应是2元,而他的价格只有1斤葱的价格1元,所以50元买走100斤葱。
正确分解葱价:
1斤葱白+1斤葱绿=2斤葱(2元)
(半斤葱白0.3+半斤0.7)×2=2
葱白0.6元 /斤 + 葱绿1.4元/斤=2元
第三题:
有十二个乒乓球形状、大小相同,其中只有一个重量与其它十一个不同,现在要求用一部没有砝码的天秤称三次,将那个重量异常的球找出来,并且知道它比其它十一个球较重还是较轻。
【答案】
首先把乒乓球按数字顺序编号:1,2,3,4,5,6,7,8,9,10,11,12。
分析:
用没有砝码的天枰称 称重,只有通过两端的平衡状态来确定轻重。轻的一端向上翘,重的一端向下沉,平衡则是两端一样重。
每次称都有3种可能:
1.左边轻;2.左边重;3.左右一样重。
称法:第一次称重后根据天枰称 显示的结果(哪一边重,或是一样重)来判别,分析出下一步的称法。要把以上三种可能出现的结果都必须考虑在内。
【第 A 1次 】: 把左边1,2,3,4号球, 右边5,6,7,8号球。
结果:
【第A1次】显示为平衡,则 异球 在9,10,11,12号中,这8个为标准球。
再用左边1,2,3,右边9,10,11称【第A2次】,
【第A2次】若平衡,则12号有异常,用12与任意一个称 【第A3次】 即可知比标准
的轻或重。(共3次)
【第A2次】不平衡,则9,10,11中有异常,且根据得知比标准的轻重情况。再将三个中任意两
个对称【第A3次】,此时若【第A3次】平衡则是9,10,11中没有参与【第A3次】
称重的。不平衡则根据【第A2次】9,10,11的上下方向与本次相同的那一端的球为
不标准的异球。(共3次)
【第A1次】结果不平衡则:9,10,11,12为标准球,异球在所称过的这8个球中。(注:在左右两边数量相等的条件下,标准球不会影响天平的平衡状态)
【第B2次】称法一:
取出3、4不参与称重
左边球号 : 1,2,5,6,7。 右边球号: 8,9,10,11,12
一:【B2次 】平衡则,异球为3,4两个中,将其对称【B3次】,再根据【A1次】称得左边的结
果上下方向相同的一端判断是哪个球。(共3次)
【B2次 】不平衡则有两种情况:
(1 )【第B2次】 和【第A1次】 的轻重方向一致,都是左边轻或重,那么,因9,10,11,12,是标准球,不会影响重量,而5,6,7,的位置改变而天枰结果没改变,推断出,5,6,7球为标准,未发生位置变换的1,2,8中有异常,将1,2球对称【B3次】平衡则是8号,不平衡则与 【B2次】 左边的结果相同的一端为异常球。(共3次)
(2)【第B2次】和【第A1次】 两端轻重 方向相反,则推断是因5,6,7发生位置变化改变了左右两端的结果,且推论出它比标准的轻重。(即:5,6,7,在A1次右边和B2次左边的结果相同。)故异常球在5,6,7中,任意对称其中2个【B3次】,
【B3次】平衡则是5,6,7号球中没有参与【B3次】称重的那个球,且根据【B2次】称重结
果已经判定他是较轻还是较重。
【B3次】不平衡则是与【B2次】的左边结果 相同 的一端的球有异常。(共3次)
改变【第B2次】称法二:
取出1 、2、3、10、11、12
号不称, 然后左边:4、5、6 ,右边 :7、8、9。
B2平衡,则是1、2、3其中一个。取任意两个对称,B3不平衡根据结果判断与A1次左边平衡状态的结果 一致的那个为异常球,B3平衡,则是没有参与称重的哪一个,且根据A1次结果判断比标准的轻或重。(共三次)
B2不平衡,结果与A1相同,则是没有发生位置变化的4、7、8,取左7、右8对称,B3不平衡 结果与A1 相反,则是左、右位置变化后的7号球,相同则是8号球,B3平衡,可知为4号球异常。。(共三次)
结果与A1次相反,则是位置发生变化的5、6异常,取左5、右6对称,结果与A1次右端一样的为异常球。
第四题:
一个商人骑一头驴要穿越1000公里长的沙漠,去卖3000根胡萝卜。已知驴一次性可驮1000根胡萝卜,但每走1公里又要吃掉1根胡萝卜。问:商人最多可卖出多少胡萝卜?
【答案】
分析:
如果每次从起点驮1000根走完全程1000km,刚好被驴吃完,没有可以卖的,所以必须分段驮。驴没走1公里吃1根胡萝卜,因此必须使驴走的总路程尽可能降低减少胡萝卜的消耗,就必须减少返回趟数,并且合理分段才能走最少的路程。最后一趟走完全程是无法缩减的,那么只能是在第一趟和第二趟上合理分段。
画线段图解,A,B,C,D依次为线段分割的标点。
第一次:从A驮1000根走250里到B ,再回到A,往返吃500根剩500根在B处,
第二次:从A驮1000根走250里吃了250根,再把B处余下的驮上250根余下250根在B处,
还是1000根从B 向前到C走250里,吃了250根,返回A吃500根余下250根在C处,
第三次:驮上最后1000根走完全程到达D点刚好够吃,走到B,C两处时分别驮上两处余下250根
的填补途中所吃的,最后就余下500根可以卖。
第五题:
话说某天一艘海盗船被天上砸下来的石头给击中了,5个倒霉的海盗只好逃难到一个孤岛,发现有棵椰子树,还有一只猴子!大家把椰子全部采摘下来放在一起,但是天已经很晚了,所以没统计数量就先睡觉了.
晚上某个家伙悄悄的起床将椰子平均分成5份,结果发现多一个椰子,顺手就给了幸运的猴子,然后又悄悄的藏了一份,把剩下的椰子混在一起放回原处,悄悄的回去睡觉了.
过了会儿,另一个家伙也悄悄的起床,将剩下的椰子分成5份,结果发现多一个椰子,顺手就又给了幸运的猴子,也悄悄的藏了一份,把剩下的椰子混在一起放回原处,也悄悄的回去睡觉了.
又过了一会 ......
又过了一会 ...
总之5个家伙都起床过,都做了同样的事情。早上大家都起床,各自心怀鬼胎的分椰子了,这个猴子还真不是一般的幸运,因为这次把椰子分成5分后居然又多一个椰子,只好又给它了.问题来了,这堆椰子最少有多少个?
【答案】
根据其条件,得知:共分了6次,由第一次的总数平均分5份余下1个。
从 第二次分椰子开始 的如下规律:
藏了一分,则第二次分的总数是第一次分得的四份的和,再分成5份还是余下1个,.........照此把上次分的的五份藏一份,用四份的和再分5份余1个,共6次。
那么得出第二次 到底五次中需满足如下条件: 4的倍数除以5余下1。 一个数除以另一个数的余数大小取决于被除数的个位, 5的倍数里的 个位 数只有“0”和“5”。那么分5份,余1个,则被除数的个位必须是“1”或“6”。(0+1=“1 ” 5+1=“6”) 但是这个数是前次分的四份的和,那么这个数必须能被“4”整除。因为:“4”的倍数关系里个位数有“6”(4X4=16, 4X9=36),任何整数乘以4的个位数不会有“1”。由此推导出第二次 开始所分的数量的个位数必须是“6”。(第一次分时的总数除外,总数个位数是5的 倍数的个位数+1.)因此,推论出
那么 可以推论出每次分得的结果(平均数)的个位数只有“4”或“9”(4X4=16, 9X4=36才能满足每次分之前的总数的个位数为“6”的条件)。 ...........假设:某次分得的是每份 9996个,代入规律公式,
设总数为Y ,最后一次分得的平均数为X得:
{[(Y-1)÷5x4-1]÷5x4-1]÷5x4-1]÷5x4-1]÷5x4-1}÷5=X
进行计算和推理,得出总数为:15621。最后一次每人分得1023个,还 余下一个给猴子。
算式:
15621 分5 份 第一次每份3124余1 ( 3124 x5+1=15621)藏1份剩4份:
3124 x4=12496 分5份 第二次每份2499余1 (2499 x5+1=12496) 藏1份剩下4份:
2499X4=9996 分5份 第三次每份1999余1 (1999 x5+1=9996)藏1份剩下4份:
1999X4=7996 分5份 第四次每份1599余1 (1599 x5+1=7996)藏1份剩下4份:
1599X4=6396 分5 份 第五次每份1279余1 (1279 x5+1=6396)藏1份剩下4份:
1279X4=5116 分5份 第六次每份1023余1 (1023 x5+1=5116)结束。
不定方程疑难问题(海盗分椰子):
古时候有一艘海盗船,突遇海难,五个海盗幸运的飘到一个岛上,但岛上很荒凉,只有一颗结满椰子的椰子树和树上的一只猴子,几个海盗把椰子全部从树上摘下来堆成一堆之后就休息了,夜间第一个海盗把这堆椰子平均分成5份,还多了一个,就把这多余的一个赐给猴子了,随后他又私藏了一份;随后第二个、第三个、第四个、第五个海盗先后都如法炮制。第二天醒来,几个海盗都都心怀鬼胎地来分椰子,平均分成5份后还多余一个,又把这多余的椰子赐给幸运的猴子了,问这棵树至少有多少颗椰子?
或者==解:设总共有Y个椰子,最后一次(第二天分时)每人分N个
第一海盗分后剩余:4/5(Y-1)
第二海盗分后剩余:4/5[ 4/5(Y-1)-1]=1/25(16Y-36)
第三海盗分后剩余:4/5[1/25(16Y-36)-1]=1/125(64Y-244)
第四海盗分后剩余:4/5[1/125(64Y-244)-1]=1/625(256Y-1476)
第五海盗分后剩余:4/5[1/625(256Y-1476)-1]=1/3125(1024Y-8404)
依据题意得:1/3125(1024Y-8404)=5N+1,
化简1024Y=15625N+11529
Y=(15625N+11529)/1024=15N+11+(265N+265)/1024
Y肯定是个正整数,上式中15N+11是正整数,那么(265N+265)/1024也必须是正整数,设N=1024P-1就能满足上述要求,将N=1024P-1带入Y:
得Y=15625P-4,当P取1时,Y获得最小值即15621个。
第六题:
国王亲自监斩四个死囚犯,定下条例:每人说句话,说真话的处以绞刑,说假话的处以砍头。
甲:我爱国王。 国王说你若爱我就不会犯下滔天罪恶,说假话给我拉出去砍了!
乙:我有罪,该死。国王说认罪伏诛,算真话处绞刑。
丙:我是未来建设国家的栋梁。国王想了想,这未来无法验证算假话,砍了!
丁:“……”国王想了很久,要维护自己的尊严兑现承诺,就不能说话不算话,不能自毁条例,没法处置丁死囚犯,就把他放了。
你知道丁死囚犯说了句什么吗?为什么国王没法杀他?
【答案】
丁说:我将被砍头。
“我将被砍头”如果是假话,他就应该被砍头。
但是他被砍头了,则他说的是真话,应该处绞刑。
处以绞刑,那么“我将被砍头”就是假话,就应该被砍头.........
如此推理,国王无法决定对他的用刑,只好放了。
第七题:说一个屋里有多个桌子,有多个人?
如果3个人一桌,多2个人。
如果5个人一桌,多4个人。
如果7个人一桌,多6个人。
如果9个人一桌,多8个人。
如果11个人一桌,正好。
请问这屋里多少人?
【答案】
分析规则为:假设总人数加上1个人就可以3人/桌,5人/桌,7人/桌,9人 /桌桌刚好的, 算出能被3,5,7,9所整除的最小公倍数315。此是“ 总数+1 ”的最小公倍数,实际“总数+1”必须满足 不能被 “11”整除,应该余1的条件。
但是315÷11=28……7。 要满足除以11余1的条件,就要用315乘以某个倍数 。根据315÷11=28……7的余数7, 推论出 余数7X8倍=56。 56除以11等于5余1,那么315X8=2520 (2520-1)÷11=229……1。
又根据5人每桌余4人,5的倍数的个位是“0”和“5”,则总人数的个位数必须是“4”或“9”。( 推论算式:9-5=4 4-0=4)
总人数的个位为“4”或“9”,那么11人每桌,其桌数的个位数也必须是“4”或“9”。
315X8=2520(总人数+1) 那么总人数为:
2520-1=2519(满足总人数个位为“9”的推论)
3人 /桌 X839桌+余2人= 2519 人
5人/桌 X503桌+余4人=2519人
7人/桌X359桌+余6人=2519人
9人/桌X279桌+余8人=2519人
11人/桌X229桌 =2519人
第八题:有人想买几套餐具,到餐具店看了后,发现自己带的钱可以买21把叉子和21把勺子,或者28把小刀。如果他买的叉子,勺子,小刀数量不统一,就无法配成套,所以他必须买同样多的叉子,勺子,小刀,并且正好将身上的钱用完。如果你是这个人,你该怎么办?
【答案】
解: 设 杈、勺的价格为 X,刀的价格为 Y,刀,杈勺配套后的数量为 Z 得:
(1) 21X+21X=28Y 解得:42X=28Y, 求出 42和28的最小公倍数是84。那么
84÷(21+21)=2 杈勺都是2元/把,
84÷28=3,刀3元/把。
(2)2Z+2Z+3Z=84 解得Z=12(把)
现在买数量相等的配套餐具,则:
12杈X2元/把+12勺X2元/把+12把刀X3元/把=84元
第九题:某学生问:老师您今年几岁啊?
老师:我像你现在这么大时,你才3岁:等你长到我现在这么大时我39岁。你说我多大?
请问他们到底各是几岁?
【答案】
分析:他们的年龄会变化,但是老师和学生之间的“年龄差距”始终不会变。
老师像学生那么大时学生才3岁,即老师的“年龄”减去他们的“年龄差”就是学生的年龄,就是要倒退这个“年龄差”的时间,那么学生也相应要后退这个“年龄差”。所以推论出学生的现在“年龄”减去“年龄差”等于“3岁”。
学生长到老师的年龄时老师39岁,学生的“年龄”加上“年龄差”等于老师的“年龄”,那么就是老师的“年龄”再加上这个“年龄差”就等于“39岁”。
推理出算式:
(1) 3+年龄差=学生年龄:
(2) 学生 年龄+年龄差=老师年龄
(3) 老师年龄+年龄差=39
根据以上3个算式,设他们的“年龄差”为 “Y”得:3+Y得学生年龄,再加“Y”得
老师年龄,再加“Y”得39。
算式为:
3+Y+Y+Y=39
解: 3Y=39-3
3Y=36
Y=12(年龄差)
学生年龄:3+12=15(岁)
老师年龄:15+12=27(岁)
第十题:一次洪灾中,一猎人带一猎狗撑船一艘去救一家,父母二女儿二儿子六口人渡河。父母和猎人会撑船,船每次限载二人(包括撑船的和猎狗)猎人不在猎狗会咬他们一家人,父亲不在母亲就打女儿,母亲不在父亲就打儿子。在保障他们都不受伤害的条件下,最少分几次渡河?如何渡?
【答案】
河分左右两岸,假设他们都在左边,
第1次: 父母共渡到右岸,父亲留下,母亲返回左岸。(此时右边有:父亲)
第2次: 母亲把1儿子送到右岸,留下儿子在右岸,
把父亲接回左岸,避免他打右边的儿子——(此时右边有: 1儿子)
第3次: 母亲送另一个儿子到右岸,自己返回左岸。 (此时右边有:2儿子)
第4次: 把父母共度到右边,母亲留在右岸,
父亲回左岸 —————— (此时右边有:2儿子和母亲)
第5次: 猎人带猎狗到右岸;自己和猎狗留右岸,
把船给母亲回左岸 ———(此时右: 2儿子,猎人,猎狗)
第6次: 父母再次共度右岸,母亲留右岸
父亲回左岸 ———————(此时右:2儿子,猎人,猎狗,母亲)
第7次: 父亲送1女到右岸,
父母亲同回左岸 ——————(此时右:2儿子,猎人,猎狗,1女儿)
第8次: 父亲送另1女到右岸,返回接母亲 ——(此时右:2儿子2女儿,猎人,猎狗)
第9次: 父亲把母亲接回右岸 ————(此时右:全部到齐!!)
大功告成!!!!!
第十一题:现在共有100匹马和100块石头,马分3种,大型马;中型马跟小型马。其中一匹大马一次可以驮3块石头,中型马可以驮2块,而小型马2头可以驮一块石头。问需要多少匹大马,中型马跟小型马才能使100匹马驮完100块石头?(问题的关键是驮100块石头刚好必须是用完100匹马)
【答案】
设:大马为X,中马为Y,小马为Z,
得方程式:1. X+Y+Z=100 (马匹的总数)
2. 3X+2y+0.5Z=100(石头的总数)
其中x,y,z均为非负整数.
解得六组数据:
① x=17, y=5, z=78
② x=14, y=10, z=76
③ x=11, y=15, z=74
④ x=8, y=20, z=72
⑤ x=5, y=25, z=70
⑥ x=2, y=30, z=68
举例第②组:大马14匹,中马10匹,小马76匹。
算式:
1.马匹总数: 14+10+76=100
2.石头总数: 3x14 + 2x10 + 0.5x76 =100
从以上6组数据找出存在的客观规律,6组数据综合后,出现数列等差X的等差为3 ,Y的等差为5 ,Z 的等差为 2。
第十二题:据说有人给酒肆的老板娘出了一个难题:此人常来,所以知道店里只有两个舀酒的勺子,分别能舀7两和11两酒,却硬要老板娘卖给他2两酒。聪明的老板娘毫不含糊,用这两个勺子在酒缸里舀酒,并倒来倒去,居然量出了2两酒,聪明的你能做到吗?
【答案】
设 :舀11两酒的勺为 "A"勺,舀7两酒的勺为 " B"勺,方法如下:
首先把 A勺 打满11两倒入空的 B 勺 里并倒满,A勺里剩下4两(11-7=4),把B勺里的全部倒回酒缸,把 A勺 里的 4两 倒入空的B勺 ,再把A勺打满11两倒3两入B勺使其刚好满,(4+3=7),A勺剩下8两(11-3=8),把B勺全部倒回酒缸,再把A勺里剩下的8两倒满B勺,此时,A勺剩下1两(8-7=1),再次把B勺全部倒回酒缸,把A勺一两倒入B勺,把A勺打满11两 倒6两入B勺使其满(6+1=7),则A勺剩下5两(11-6=5),把B勺全部倒回酒缸,把A勺里剩下的5两倒入B勺, 再把A勺打满11两倒入2两B里使其满(5+2=7),A勺剩下9两(11-2=9),再把B勺全部倒回酒缸,把A勺里剩下的9两倒满B勺,这时A勺里剩下的就是2两酒
9-7=2
(A勺共从酒缸里打满酒四次,4x11=44 两。B勺通过A勺倒酒6次,7x6=42 两, 44 - 42=2两)
如果客人要3两酒,那么(11×6)-(7×9)=3 同上循环,将A勺打满6次,向B勺倒酒9次便可得出3两酒。
这样的容器要抓住容积数据的特性,两个容器不同容积,容值同为奇数,则其差数为 偶数,利用容器之间的 差额可 求得奇数和 偶数的数值;若容量都是偶数,直接差数为 偶数,那么就 无法求得奇数数值。6和9 这 两个容量为奇数、偶数混搭的容器,求得的只能是其最小 公约数3 的倍数数值,无法获得不能 被 3整除的任何数值。
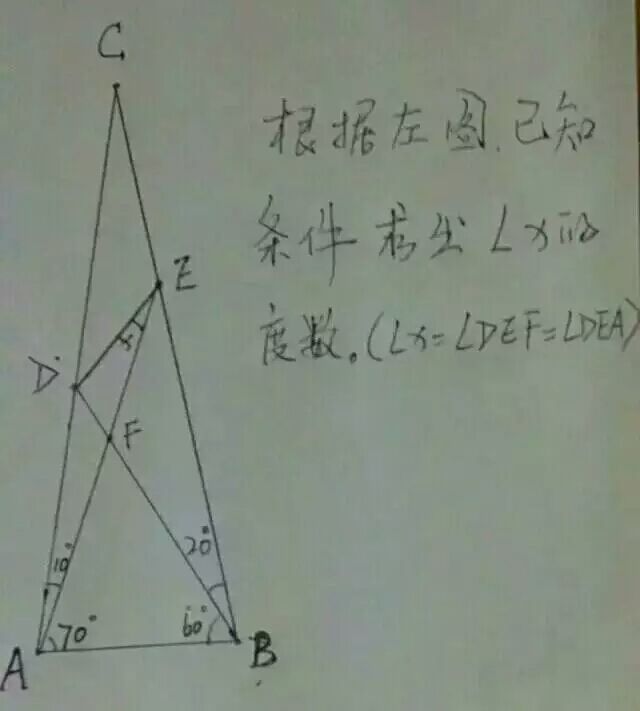
【几何题一】
解:
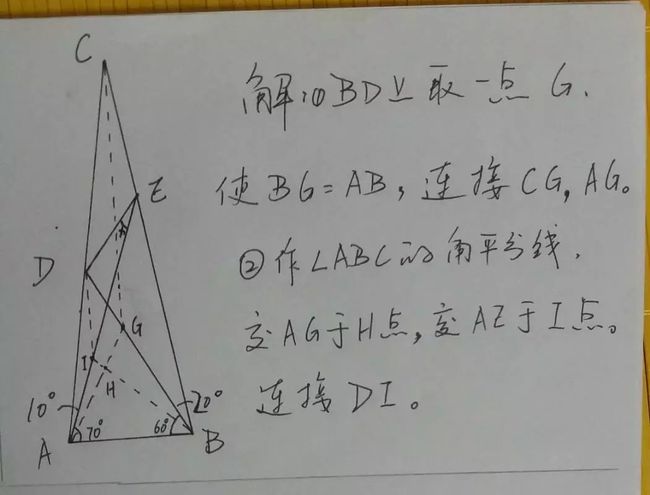
①在BD上截取BG=AB,分别连接CG,AG,
②作∠ABC的角平分线交AG于H点,交AE于I点。
∵IB是∠ABC的角平分线,
∴∠CBI=IBA=40°,
∠DBI=∠CBI-∠CBD=40°-20°=20°
三角形ABI中,∠IAB=70°,
∠IBA=40°,
∠AIB=180°-70°-40°=70°
∠AIB=IAB=70°,
∴三角形ABI是等腰三角形,AB=IB。
∵ABC中,
∠CAB=∠CAE+∠EAB=10°+70°=80°
∠CBA=∠CBD+∠DBA=20°+60°=80°
∴三角形ABC是等腰三角形。AC=BC.,∠ACB=20°
∵CDB中,∠ACB=20°
(已证)∠CBD=20°(已知)
∴三角形CDB是等腰三角形,CD=BD。
∵ABG中,∠DBA=60°,
BG=AB,
∠BAG=∠BGA=60°=∠DBA,
三角形ABG是等边三角形,
∴三条边BG=AG=AB=IB。
∠CAG=∠CAE+∠EAG
=10°+(70°-60°)
=20°
三角形AGC和三角形BGC中,
AC=BC (已证)
AG=BG(已证)
CG=CG(公共边)
∴三角形AGC≌三角形BGC,
∠ACG=BCG=10°。
三角形AEC和三角形CGA中:
∠CAE=∠ACG=10°
CA=AC(公共边)
∠ACE=CAG=20°
∴三角形AEC≌三角形CGA,
边CE=AG=GB=AB=IB。
三角形CDE和 三角形 BDI中:
CE=IB
∠DCE=DBI=20°
CD=BD
∴三角形CDE≌ 三角形 BDI
DE=DI,∠EDC=∠IDB。
三角形ABD中,
∠ADB=180°-70°-10°-60°=40°(三角形内角和定理)
∠CDB=180°-∠ADB=180°-40°=140°
∠CDB=∠EDC+∠EDB=140°
∵∠EDC=∠IDB,
∴∠EDC+∠EDB=∠IDB+∠EDB=140°=∠IDE(等量代换)
三角形IDE中,
DE=ID,
∠DEI=DIE=(180°-∠IDE)÷2=(180°-140)÷2=20°
∠DEI=∠DEA=∠X=20°
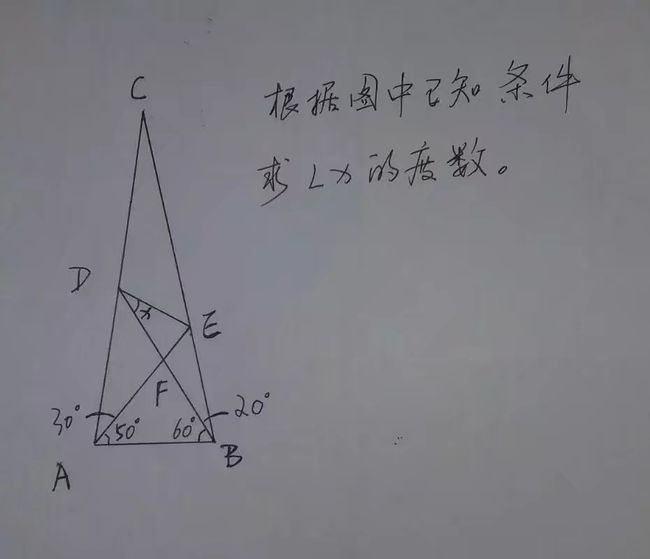
【几何题二】
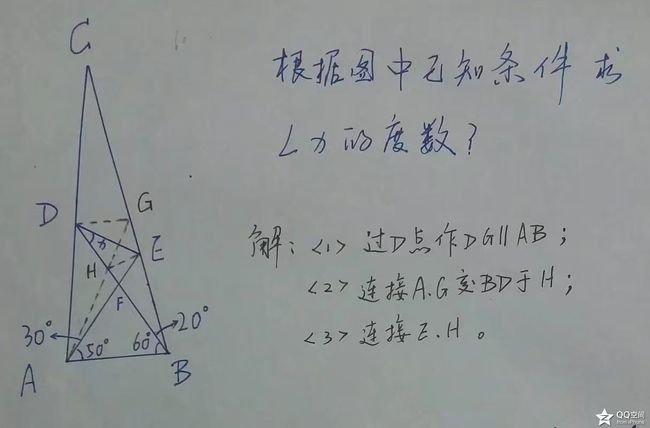
解法【一】
解:(1)过D点作DG∥AB;
(2)连接A、G交BD于H;
(3)连接E、H。
∵四边形ABGD 中
∠DAB=∠DAE+∠EAB
= 30°+50°
=80°
∠GBA=∠GBD+∠DBA
= 20°+60°
=80°
又∵DG∥AB
∴四边形ABGD是等腰梯形
AD=BG
AG=BD(等腰梯形对角线定理)
ABD 、BAG 中
∵AD=BG(已证)
BD=AG(已证)
AB=BA(公共边)
ABD≌BAG (SSS)
∴∠BGA=∠ADB
=180°-(30°+50°+60°)
=40 °(三角形内角和定理)
∠ABD=∠BAG=60°(等边对等角)
∠AHB=180°-∠ABD-∠BAG
=180°-60°-60°
=60°(三角形内角和定理)
∵ABH中
∠ABD=∠BAG=∠AHB=60°(已证)
∴ABH是等边三角形
AH=AB=BH
∴ABH∽DGH (平行线内错角相等+对顶角相等)
DGH是等边三角形
GD=HD=HG
∠GDH=∠DGH=∠DHG=60°
∵EBA中
∠BEA=180°-∠EAB-∠EBA
=180°-50°-80°
=50°
∠BEA=∠EAB=50°
∴EBA是等腰三角形
AB=BE(等角对等边)
∵AH=AB=BH(已证)
∴AH=AB=BH=BE
∠EHB=∠HEB=(180D°-∠EBH)÷2
=(180°-20°)÷2
=80°
EGH中
∠GHE=180°-∠DHG-∠EHB
=180°-60°-80°
=40°
∠GHE=∠BGA=∠EGH
∴EGH是等腰三角形
EG=EH
EGD 、EHD中
GD=HD(已证)
EG=EH(已证)
DE=DE (公共边)
∴ EGD ≌EHD(SSS)
∠EDG=∠EDH(等边对等角)
=∠GDH÷2
∵DG∥AB
∴∠CDG=∠CAB=80°
∠GDH=180°-(∠CDG+∠ADB)
=180°-(80°+40°)
=60°(补角定理)
∠X=∠EDH=∠GDH÷2
∠X =60°÷2
∠X=30 °
解法2【二】
解:
①以B点为圆心,AB为半径,顺时针旋转AB交AC于G点,可知 BG=BA。
②链接EG
根据已知条件
三角形A BG中,
∵BG=BA,
∴∠BGA= ∠BAG
=∠CAE+∠BAE
=30°+50°=80°
∴∠ABG=180°-(∠BGA+∠BAG)
=180°-160°
=20°
∵三角形 ABE中,
∠AEB=180°-∠EAB-∠EBA
=180°-50°-(20°+60°)
=50°
∴ABE是等腰三角形
BA=BE=BG
∵三角形 EBG中,
BE=BG(已证)
∴∠BEG=∠BGE
∠EBG=∠ABC-∠ABG
=(20°+60°)-20°
=60°
∴∠BEG=∠BGE
=(180°-60°)÷2
=60°
∴三角形EBG是等边三角形
BE=EG=BG
三角形DGB中,
∠GDB=∠DAB
=180°-(30°+50°+60°)
=40°
∠GBD=∠DBA-∠ABG
=60°-20°
=40°
∴∠GDB= ∠GBD=40°
∴DGB为等腰三角形
DG=DB=BG=EG=BE=BA
三角形DGE中,
∵DG=EG(已证)
∴∠GDE=∠GED
∠DGE=180°-(∠BGA+∠BGE)
=180°-(80°+60°)
=40°
∠GDE=∠GED=(180°-40°)÷2
=70°
∠X=∠EDB
=∠GDE-∠ADB
=70°-[180°-(30°+50°+60°)]
∠X =70°-40°
∠X=30°