列表是 Lisp 的基本数据结构之一。在最早的 Lisp 方言里,列表是唯一的数据结构: “Lisp” 这个名字起初是 “LISt Processor” 的缩写。但 Lisp 已经超越这个缩写很久了。 Common Lisp 是一个有着各式各样数据结构的通用性程序语言。
3.1 构造
在 2.4 节我们介绍了 cons , car , 以及 cdr ,基本的 List 操作函数。 cons 真正所做的事情是,把两个对象结合成一个有两部分的对象,称之为 Cons 对象。概念上来说,一个 Cons 是一对指针;第一个是 car ,第二个是 cdr 。
Cons 对象提供了一个方便的表示法,来表示任何类型的对象。一个 Cons 对象里的一对指针,可以指向任何类型的对象,包括 Cons 对象本身。它利用到我们之后可以用 cons 来构造列表的可能性。
我们往往不会把列表想成是成对的,但它们可以这样被定义。任何非空的列表,都可以被视为一对由列表第一个元素及列表其余元素所组成的列表。 Lisp 列表体现了这个概念。我们使用 Cons 的一半来指向列表的第一个元素,然后用另一半指向列表其余的元素(可能是别的 Cons 或 nil )。 Lisp 的惯例是使用 car 代表列表的第一个元素,而用 cdr 代表列表的其余的元素。所以现在 car 是列表的第一个元素的同义词,而 cdr 是列表的其余的元素的同义词。列表不是不同的对象,而是像 Cons 这样的方式连结起来。
当我们想在 nil 上面建立东西时,
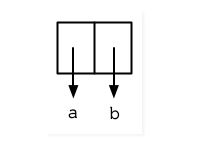
> (setf x (cons 'a nil))
(A)
产生的列表由一个 Cons 所组成,见图 3.1。这种表达 Cons 的方式叫做箱子表示法 (box notation),因为每一个 Cons 是用一个箱子表示,内含一个 car 和 cdr的指针。当我们调用 car 与 cdr 时,我们得到指针指向的地方:
> (car x)
A
> (cdr x)
NIL
当我们构造一个多元素的列表时,我们得到一串 Cons (a chain of conses):
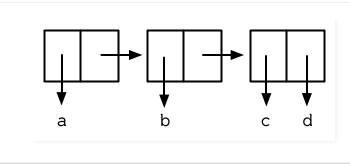
> (setf y (list 'a 'b 'c))
(A B C)
产生的结构见图 3.2。现在当我们想得到列表的 cdr 时,它是一个两个元素的列表。
在一个有多个元素的列表中, car 指针让你取得元素,而 cdr 让你取得列表内其余的东西。
一个列表可以有任何类型的对象作为元素,包括另一个列表:
> (setf z (list 'a (list 'b 'c) 'd))
(A (B C) D)
当这种情况发生时,它的结构如图 3.3 所示;第二个 Cons 的 car 指针也指向一个列表:
>(car (cdr z))
(B C)
前两个我们构造的列表都有三个元素;只不过 z 列表的第二个元素也刚好是一个列表。像这样的列表称为嵌套列表,而像 y 这样的列表称之为平坦列表 (flatlist)。
如果参数是一个 Cons 对象,函数 consp 返回真。所以我们可以这样定义 listp :
>(defun our-listp (x)
(or (null x) (consp x)))
因为所有不是 Cons 对象的东西,就是一个原子 (atom),判断式 atom 可以这样定义:
>(defun our-atom (x) (not (consp x)))
注意, nil 既是一个原子,也是一个列表。
3.2 等式 (Equality)
每一次你调用 cons 时, Lisp 会配置一块新的内存给两个指针。所以如果我们用同样的参数调用 cons 两次,我们得到两个数值看起来一样,但实际上是两个不同的对象:
CL-USER> (eql (cons 'a nil) (cons 'a nil))
NIL
如果我们也可以询问两个列表是否有相同元素,那就很方便了。 Common Lisp 提供了这种目的另一个判断式: equal 。而另一方面 eql 只有在它的参数是相同对象时才返回真,
CL-USER> (setf x (cons 'a nil))
(A)
CL-USER> (eql x x)
T
本质上 equal 若它的参数打印出的值相同时,返回真
CL-USER> (equal x (cons 'a nil))
T
这个判断式对非列表结构的别种对象也有效,但一种仅对列表有效的版本可以这样定义:
CL-USER> (defun our-equal (x y)
(or (eql x y)
(and (consp x)
(consp y)
(our-equal (car x) (car y))
(our-equal (cdr x) (cdr y)))))
这个定义意味着,如果某个 x 和 y 相等( eql ),那么他们也相等( equal )。
勘误: 这个版本的 our-equal 可以用在符号的列表 (list of symbols),而不是列表 (list)。
3.3 为什么 Lisp 没有指针 (Why Lisp Has No Pointers)
一个理解 Lisp 的秘密之一是意识到变量是有值的,就像列表有元素一样。如同 Cons 对象有指针指向他们的元素,变量有指针指向他们的值。
你可能在别的语言中使用过显式指针 (explicitly pointer)。在 Lisp,你永远不用这么做,因为语言帮你处理好指针了。我们已经在列表看过这是怎么实现的。同样的事情发生在变量身上。举例来说,假设我们想要把两个变量设成同样的列表:
CL-USER> (setf x '(a b c))
(A B C)
CL-USER> (setf y x)
(A B C)
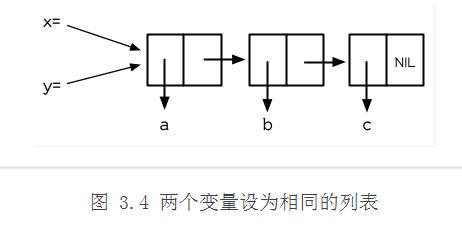
当我们把 x 的值赋给 y 时,究竟发生什么事呢?内存中与 x 有关的位置并没有包含这个列表,而是一个指针指向它。当我们给 y 赋一个相同的值时, Lisp 复制的是指针,而不是列表。(图 3.4 显式赋值 x 给 y 后的结果)无论何时,你将某个变量的值赋给另个变量时,两个变量的值将会是 eql 的:
CL-USER> (eql x y)
T
Lisp 没有指针的原因是因为每一个值,其实概念上来说都是一个指针。当你赋一个值给变量或将这个值存在数据结构中,其实被储存的是指向这个值的指针。当你要取得变量的值,或是存在数据结构中的内容时, Lisp 返回指向这个值的指针。但这都在台面下发生。你可以不加思索地把值放在结构里,或放“在”变量里。
为了效率的原因, Lisp 有时会选择一个折衷的表示法,而不是指针。举例来说,因为一个小整数所需的内存空间,少于一个指针所需的空间,一个 Lisp 实现可能会直接处理这个小整数,而不是用指针来处理。但基本要点是,程序员预设可以把任何东西放在任何地方。除非你声明你不愿这么做,不然你能够在任何的数据结构,存放任何类型的对象,包括结构本身。
3.4 建立列表 (Building Lists)
函数 copy-list 接受一个列表,然后返回此列表的复本。新的列表会有同样的元素,但是装在新的 Cons 对象里:
CL-USER> (setf x '(a b c)
y (copy-list x))
(A B C)
图 3.5 展示出结果的结构; 返回值像是有着相同乘客的新公交。我们可以把 copy-list 想成是这么定义的:
CL-USER> (defun our-copy-list (lst)
(if (atom lst)
lst
(cons (car lst) (our-copy-list (cdr lst)))))
这个定义暗示着 x 与 (copy-list x) 会永远 equal ,并永远不 eql ,除非 x 是 NIL 。
最后,函数 append 返回任何数目的列表串接 (concatenation):
CL-USER> (append '(a b) '(c d) 'e)
(A B C D . E)
通过这么做,它复制所有的参数,除了最后一个
3.5 示例:压缩 (Example: Compression)
作为一个例子,这节将演示如何实现简单形式的列表压缩。这个算法有一个令人印象深刻的名字,游程编码(run-length encoding)。
在餐厅的情境下,这个算法的工作方式如下。一个女服务生走向有四个客人的桌子。“你们要什么?” 她问。“我要特餐,” 第一个客人说。 “我也是,” 第二个客人说。“听起来不错,” 第三个客人说。每个人看着第四个客人。 “我要一个 cilantro soufflé,” 他小声地说。 (译注:蛋奶酥上面洒香菜跟酱料)
瞬息之间,女服务生就转身踩着高跟鞋走回柜台去了。 “三个特餐,” 她大声对厨师说,“还有一个香菜蛋奶酥。”
图 3.6 展示了如何实现这个压缩列表演算法。函数 compress 接受一个由原子组成的列表,然后返回一个压缩的列表:
CL-USER> (compress '(1 1 1 0 1 0 0 0 0 1))
((3 1) 0 1 (4 0) 1)
当相同的元素连续出现好几次,这个连续出现的序列 (sequence)被一个列表取代,列表指明出现的次数及出现的元素。
主要的工作是由递归函数 compr 所完成。这个函数接受三个参数: elt , 上一个我们看过的元素; n ,连续出现的次数;以及 lst ,我们还没检查过的部分列表。如果没有东西需要检查了,我们调用 n-elts 来取得 n elts 的表示法。如果 lst 的第一个元素还是 elt ,我们增加出现的次数 n 并继续下去。否则我们得到,到目前为止的一个压缩的列表,然后 cons 这个列表在 compr 处理完剩下的列表所返回的东西之上。
要复原一个压缩的列表,我们调用 uncompress (图 3.7)
CL-USER> (uncompress '((3 1) 0 1 (4 0) 1))
(1 1 1 0 1 0 0 0 0 1)
这个函数递归地遍历这个压缩列表,逐字复制原子并调用 list-of ,展开成列表。
CL-USER> (list-of 3 'ho)
(HO HO HO)
我们其实不需要自己写 list-of 。内置的 make-list 可以办到一样的事情 ── 但它使用了我们还没介绍到的关键字参数 (keyword argument)。
图 3.6 跟 3.7 这种写法不是一个有经验的Lisp 程序员用的写法。它的效率很差,它没有尽可能的压缩,而且它只对由原子组成的列表有效。在几个章节内,我们会学到解决这些问题的技巧。
载入程序
在这节的程序是我们第一个实质的程序。
当我们想要写超过数行的函数时,
通常我们会把程序写在一个文件,
然后使用 load 让 Lisp 读取函数的定义。
如果我们把图 3.6 跟 3.7 的程序,
存在一个文件叫做,“compress.lisp”然后输入
(load "compress.lisp")
到顶层,或多或少的,
我们会像在直接输入顶层一样得到同样的效果。
注意:在某些实现中,Lisp 文件的扩展名会是“.lsp”而不是“.lisp”
3.6 存取 (Access)
Common Lisp 有额外的存取函数,它们是用 car 跟 cdr 所定义的。要找到列表特定位置的元素,我们可以调用 nth ,
CL-USER> (nth 0 '(a b c))
A
而要找到第 n 个 cdr ,我们调用 nthcdr :
CL-USER> (nthcdr 2 '(a b c d))
(C D)
nth 与 nthcdr 都是零索引的 (zero-indexed); 即元素从 0 开始编号,而不是从 1 开始。在 Common Lisp 里,无论何时你使用一个数字来参照一个数据结构中的元素时,都是从 0 开始编号的。
两个函数几乎做一样的事; nth 等同于取 nthcdr 的 car 。没有检查错误的情况下, nthcdr 可以这么定义:
(defun our-nthcdr (n lst)
(if (zerop n)
lst
(our-nthcdr (- n 1) (cdr lst))))
函数 zerop 仅在参数为零时,才返回真。
函数 last 返回列表的最后一个 Cons 对象:
CL-USER> (last '(a b c))
(C)
这跟取得最后一个元素不一样。要取得列表的最后一个元素,你要取得 last 的 car 。
Common Lisp 定义了函数 first 直到 tenth 可以取得列表对应的元素。这些函数不是 零索引的 (zero-indexed):
(second x) 等同于 (nth 1 x) 。
此外, Common Lisp 定义了像是 caddr 这样的函数,它是 cdr 的 cdr 的 car 的缩写 ( car of cdr of cdr )。所有这样形式的函数 cxr ,其中 x 是一个字符串,最多四个 a 或 d ,在 Common Lisp 里都被定义好了。使用 cadr 可能会有异常 (exception)产生,在所有人都可能会读的代码里使用这样的函数,可能不是个好主意。
3.7 映射函数 (Mapping Functions)
Common Lisp 提供了数个函数来对一个列表的元素做函数调用。最常使用的是 mapcar ,接受一个函数以及一个或多个列表,并返回把函数应用至每个列表的元素的结果,直到有的列表没有元素为止:
CL-USER> (mapcar #'(lambda (x) (+ x 10))
'(1 2 3))
(11 12 13)
CL-USER> (mapcar #'list
'(a b c)
'(1 2 3 4))
((A 1) (B 2) (C 3))
相关的 maplist 接受同样的参数,将列表的渐进的下一个 cdr 传入函数。
CL-USER> (maplist #'(lambda (x) x)
'(a b c))
((A B C) (B C) (C))
其它的映射函数,包括 mapc 我们在 89 页讨论(译注:5.4 节最后),以及 mapcan 在 202 页(译注:12.4 节最后)讨论。
笔记:这一节不怎么看得懂 - -! 先过吧。
3.8 树 (Trees)
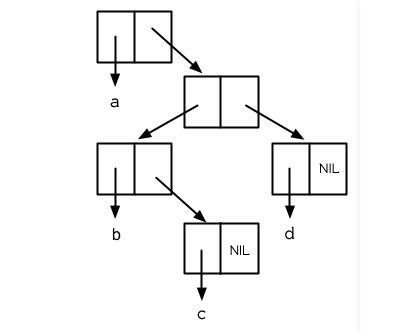
Cons 对象可以想成是二叉树, car 代表左子树,而 cdr 代表右子树。举例来说,列表
(a (b c) d) 也是一棵由图 3.8 所代表的树。 (如果你逆时针旋转 45 度,你会发现跟图 3.3 一模一样)
Common Lisp 有几个内置的操作树的函数。举例来说, copy-tree 接受一个树,并返回一份副本。它可以这么定义:
CL-USER> (defun our-copy-tree (tr)
(if (atom tr)
tr
(cons (our-copy-tree (car tr))
(our-copy-tree (cdr tr)))))
把这跟 36 页的 copy-list 比较一下; copy-tree 复制每一个 Cons 对象的 car 与 cdr ,而 copy-list 仅复制 cdr 。
没有内部节点的二叉树没有太大的用处。 Common Lisp 包含了操作树的函数,不只是因为我们需要树这个结构,而是因为我们需要一种方法,来操作列表及所有内部的列表。举例来说,假设我们有一个这样的列表:
(and (integerp x) (zerop (mod x 2)))
而我们想要把各处的 x 都换成 y 。调用 substitute 是不行的,它只能替换序列 (sequence)中的元素:
CL-USER> (substitute 'y 'x '(and (integerp x) (zerop (mod x 2))))
(AND (INTEGERP X) (ZEROP (MOD X 2)))
这个调用是无效的,因为列表有三个元素,没有一个元素是 x 。我们在这所需要的是 subst ,它替换树之中的元素。
如果我们定义一个 subst 的版本,它看起来跟 copy-tree 很相似:
CL-USER> (subst 'y 'x '(and (integerp x) (zerop (mod x 2))))
(AND (INTEGERP Y) (ZEROP (MOD Y 2)))
如果我们定义一个 subst 的版本,它看起来跟 copy-tree 很相似:
CL-USER> (defun our-subst (new old tree)
(if (eql tree old)
new
(if (atom tree)
tree
(cons (our-subst new old (car tree))
(our-subst new old (cdr tree))))))
操作树的函数通常有这种形式, car 与 cdr 同时做递归。这种函数被称之为是 双重递归 (doubly recursive)
3.9 理解递归 (Understanding Recursion)
学生在学习递归时,有时候是被鼓励在纸上追踪 (trace)递归程序调用 (invocation)的过程。 (288页「译注:附录 A 追踪与回溯」可以看到一个递归函数的追踪过程。)但这种练习可能会误导你:一个程序员在定义一个递归函数时,通常不会特别地去想函数的调用顺序所导致的结果。
如果一个人总是需要这样子思考程序,递归会是艰难的、没有帮助的。递归的优点是它精确地让我们更抽象地来设计算法。你不需要考虑真正函数时所有的调用过程,就可以判断一个递归函数是否是正确的。
要知道一个递归函数是否做它该做的事,你只需要问,它包含了所有的情况吗?举例来说,下面是一个寻找列表长度的递归函数:
CL-USER> (defun len (lst)
(if (null lst)
0
(+ (len (cdr lst)) 1)))
我们可以借由检查两件事情,来确信这个函数是正确的:
1)对长度为 0 的列表是有效的。
2)给定它对于长度为 n 的列表是有效的,它对长度是 n+1 的列表也是有效的。
如果这两点是成立的,我们知道这个函数对于所有可能的列表都是正确的。
我们的定义显然地满足第一点:如果列表( lst ) 是空的( nil ),函数直接返回 0 。现在假定我们的函数对长度为 n 的列表是有效的。我们给它一个 n+1 长度的列表。这个定义说明了,函数会返回列表的 cdr 的长度再加上 1 。 cdr 是一个长度为 n 的列表。我们经由假定可知它的长度是 n 。所以整个列表的长度是 n+1。
我们需要知道的就是这些。理解递归的秘密就像是处理括号一样。你怎么知道哪个括号对上哪个?你不需要这么做。你怎么想像那些调用过程?你不需要这么做。
更复杂的递归函数,可能会有更多的情况需要讨论,但是流程是一样的。举例来说, 41 页的 our-copy-tree ,我们需要讨论三个情况: 原子,单一的 Cons 对象, n+1 的 Cons 树。
能够判断一个递归函数是否正确只不过是理解递归的上半场,下半场是能够写出一个做你想做的事情的递归函数。 6.9 节讨论了这个问题。
3.10 集合 (Sets)
列表是表示小集合的好方法。列表中的每个元素都代表了一个集合的成员:
CL-USER> (member 'b '(a b c))
(B C)
当 member 要返回“真”时,与其仅仅返回 t ,它返回由寻找对象所开始的那部分。逻辑上来说,一个 Cons 扮演的角色和 t 一样,而经由这么做,函数返回了更多资讯。
一般情况下, member 使用 eql 来比较对象。你可以使用一种叫做关键字参数的东西来重写缺省的比较方法。多数的 Common Lisp 函数接受一个或多个关键字参数。这些关键字参数不同的地方是,他们不是把对应的参数放在特定的位置作匹配,而是在函数调用中用特殊标签,称为关键字,来作匹配。一个关键字是一个前面有冒号的符号。
一个 member 函数所接受的关键字参数是 :test 参数。
如果你在调用 member 时,传入某个函数作为 :test 参数,那么那个函数就会被用来比较是否相等,而不是用 eql 。所以如果我们想找到一个给定的对象与列表中的成员是否相等( equal ),我们可以:
CL-USER> (member '(a) '((a) (z)) :test #'equal)
((A) (Z))
关键字参数总是选择性添加的。如果你在一个调用中包含了任何的关键字参数,他们要摆在最后; 如果使用了超过一个的关键字参数,摆放的顺序无关紧要。
另一个 member 接受的关键字参数是 :key 参数。借由提供这个参数,你可以在作比较之前,指定一个函数运用在每一个元素:
CL-USER> (member 'a '((a b) (c d)) :key #'car)
((A B) (C D))
在这个例子里,我们询问是否有一个元素的 car 是 a 。
如果我们想要使用两个关键字参数,我们可以使用其中一个顺序。下面这两个调用是等价的:
CL-USER> (member 2 '((1) (2)) :key #'car :test #'equal)
((2))
CL-USER> (member 2 '((1) (2)) :test #'equal :key #'car)
((2))
两者都询问是否有一个元素的 car 等于( equal ) 2。
如果我们想要找到一个元素满足任意的判断式像是── oddp ,奇数返回真──我们可以使用相关的 member-if :
CL-USER> (member-if #'oddp '(2 3 4))
(3 4)
我们可以想像一个限制性的版本 member-if 是这样写成的:
CL-USER> (defun our-member-if (fn lst)
(and (consp lst)
(if (funcall fn (car lst))
lst
(our-member-if fn (cdr lst)))))
函数 adjoin 像是条件式的 cons 。它接受一个对象及一个列表,如果对象还不是列表的成员,才构造对象至列表上。
CL-USER> (adjoin 'b '(a b c))
(A B C)
CL-USER> (adjoin 'z '(a b c))
(Z A B C)
通常的情况下它接受与 member 函数同样的关键字参数。
集合论中的并集 (union)、交集 (intersection)以及补集 (complement)的实现,是由函数 union 、 intersection 以及 set-difference 。
这些函数期望两个(正好 2 个)列表(一样接受与 member 函数同样的关键字参数)。
CL-USER> (union '(a b c) '(c b s))
(A C B S)
CL-USER> (intersection '(a b c) '(b b c))
(C B)
CL-USER> (set-difference '(a b c d e) '(b e))
(D C A)
3.11 序列 (Sequences)
另一种考虑一个列表的方式是想成一系列有特定顺序的对象。在 Common Lisp 里,序列( sequences )包括了列表与向量 (vectors)。本节介绍了一些可以运用在列表上的序列函数。更深入的序列操作在 4.4 节讨论。
函数 length 返回序列中元素的数目。
CL-USER> (length '(a b c))
3
我们在 24 页 (译注:2.13节 our-length )写过这种函数的一个版本(仅可用于列表)。
要复制序列的一部分,我们使用 subseq 。第二个(需要的)参数是第一个开始引用进来的元素位置,第三个(选择性)参数是第一个不引用进来的元素位置。
CL-USER> (subseq '(a b c d) 1 2)
(B)
CL-USER> (subseq '(a b c d) 1)
(B C D)
如果省略了第三个参数,子序列会从第二个参数给定的位置引用到序列尾端。
函数 reverse 返回与其参数相同元素的一个序列,但顺序颠倒。
CL-USER> (reverse '(a b c))
(C B A)
一个回文 (palindrome) 是一个正读反读都一样的序列 —— 举例来说, (abba) 。如果一个回文有偶数个元素,那么后半段会是前半段的镜射 (mirror)。使用length 、 subseq 以及 reverse ,我们可以定义一个函数
CL-USER> (defun mirror? (s)
(let ((len (length s)))
(and (evenp len)
(let ((mid (/ len 2)))
(equal (subseq s 0 mid)
(reverse (subseq s mid)))))))
来检测是否是回文:
CL-USER> (mirror? '(a b b a))
T
CL-USER> (mirror? '(a b a))
NIL
Common Lisp 有一个内置的排序函数叫做 sort 。它接受一个序列及一个比较两个参数的函数,返回一个有同样元素的序列,根据比较函数来排序:
CL-USER> (sort '(0 2 1 3 8) #'>)
(8 3 2 1 0)
你要小心使用 sort ,因为它是破坏性的(destructive)。考虑到效率的因素, sort 被允许修改传入的序列。所以如果你不想你本来的序列被改动,传入一个副本。
使用 sort 及 nth ,我们可以写一个函数,接受一个整数 n ,返回列表中第 n 大的元素:
CL-USER> (defun nthmost (n lst)
(nth (- n 1)
(sort (copy-list lst) #'>)))
我们把整数减一因为 nth 是零索引的,但如果 nthmost 是这样的话,会变得很不直观。
CL-USER> (nthmost 2 '(0 2 1 3 8))
3
函数 every 和 some 接受一个判断式及一个或多个序列。当我们仅输入一个序列时,它们测试序列元素是否满足判断式:
CL-USER> (every #'oddp '(1 3 5))
T
CL-USER> (some #'evenp '(1 2 3))
T
如果它们输入多于一个序列时,判断式必须接受与序列一样多的元素作为参数,而参数从所有序列中一次提取一个:
CL-USER> (every #'> '(1 3 5) '(0 2 4))
T
如果序列有不同的长度,最短的那个序列,决定需要测试的次数。
3.12 栈 (Stacks)
用 Cons 对象来表示的列表,很自然地我们可以拿来实现下推栈 (pushdown stack)。这太常见了,以致于 Common Lisp 提供了两个宏给堆使用: (push x y)把 x 放入列表 y 的前端。而 (pop x) 则是将列表 x 的第一个元素移除,并返回这个元素。
两个函数都是由 setf 定义的。如果参数是常数或变量,很简单就可以翻译出对应的函数调用。
表达式
(push obj lst)
等同于
(setf lst (cons obj lst))
而表达式
(pop lst)
等同于
CL-USER> (let ((x (car lst)))
(setf lst (cdr lst))
x)
所以,举例来说:
CL-USER> (setf x '(b))
(B)
CL-USER> (push 'a x)
(A B)
CL-USER> (setf y x )
(A B)
CL-USER> (pop x)
;Compiler warnings :
; In an anonymous lambda form: Undeclared free variable X (3 references)
A
CL-USER> x
(B)
CL-USER> y
(A B)
以上,全都遵循上述由 setf 所给出的相等式。图 3.9 展示了这些表达式被求值后的结构。
3.13 点状列表 (Dotted Lists)
调用 list 所构造的列表,这种列表精确地说称之为正规列表(properlist )。一个正规列表可以是 NIL 或是 cdr 是正规列表的 Cons 对象。也就是说,我们可以定义一个只对正规列表返回真的判断式:
CL-USER> (defun proper-list? (x)
(or (null x)
(and (consp x)
(proper-list? (cdr x)))))
至目前为止,我们构造的列表都是正规列表。
然而, cons 不仅是构造列表。无论何时你需要一个具有两个字段 (field)的列表,你可以使用一个 Cons 对象。你能够使用 car 来参照第一个字段,用 cdr 来参照第二个字段。
CL-USER> (setf pair (cons 'a 'b))
(A . B)
因为这个 Cons 对象不是一个正规列表,它用点状表示法来显示。在点状表示法,每个 Cons 对象的 car 与 cdr 由一个句点隔开来表示。这个 Cons 对象的结构展示在图 3.10 。
一个非正规列表的 Cons 对象称之为点状列表 (dotted list)。这不是个好名字,因为非正规列表的 Cons 对象通常不是用来表示列表:(a . b) 只是一个有两部分的数据结构。
你也可以用点状表示法表示正规列表,但当 Lisp 显示一个正规列表时,它会使用普通的列表表示法:
CL-USER> '(a . (b . (c . nil)))
(A B C)
顺道一提,注意列表由点状表示法与图 3.2 箱子表示法的关联性。
还有一个过渡形式 (intermediate form)的表示法,介于列表表示法及纯点状表示法之间,对于 cdr 是点状列表的 Cons 对象:
CL-USER> (cons 'a (cons 'b (cons 'c 'd)))
(A B C . D)
这样的 Cons 对象看起来像正规列表,除了最后一个 cdr 前面有一个句点。这个列表的结构展示在图 3.11 ; 注意它跟图3.2 是多么的相似。
所以实际上你可以这么表示列表 (a b) ,
(a . (b . nil))
(a . (b))
(a b . nil)
(a b)
虽然 Lisp 总是使用后面的形式,来显示这个列表。
3.14 关联列表 (Assoc-lists)
用 Cons 对象来表示映射 (mapping)也是很自然的。一个由 Cons 对象组成的列表称之为关联列表(assoc-listor alist)。这样的列表可以表示一个翻译的集合,举例来说:
CL-USER> (setf trans '((+ . "add") (- . "subtract")))
((+ . "add") (- . "subtract"))
关联列表很慢,但是在初期的程序中很方便。 Common Lisp 有一个内置的函数 assoc ,用来取出在关联列表中,与给定的键值有关联的 Cons 对:
CL-USER> (assoc '+ trans)
(+ . "add")
CL-USER> (assoc '* trans)
NIL
如果 assoc 没有找到要找的东西时,返回 nil 。
我们可以定义一个受限版本的 assoc :
CL-USER> (defun our-assoc (key alist)
(and (consp alist)
(let ((pair (car alist)))
(if (eql key (car pair))
pair
(our-assoc key (cdr alist))))))
和 member 一样,实际上的 assoc 接受关键字参数,包括 :test 和 :key 。 Common Lisp 也定义了一个 assoc-if 之于 assoc ,如同 member-if 之于 member一样。
3.15 示例:最短路径 (Example: Shortest Path)
图 3.12 包含一个搜索网络中最短路径的程序。函数 shortest-path 接受一个起始节点,目的节点以及一个网络,并返回最短路径,如果有的话。
在这个范例中,节点用符号表示,而网络用含以下元素形式的关联列表来表示:
(node . neighbors)
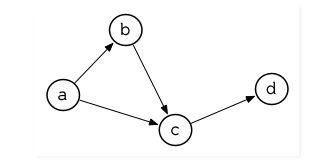
所以由图 3.13 展示的最小网络 (minimal network)可以这样来表示:
(setf min '((a b c) (b c) (c d)))
要找到从节点 a 可以到达的节点,我们可以:
CL-USER> (cdr (assoc 'a min))
(B C)
图 3.12 程序使用广度优先的方式搜索网络。要使用广度优先搜索,你需要维护一个含有未探索节点的队列。每一次你到达一个节点,检查这个节点是否是你要的。如果不是,你把这个节点的子节点加入队列的尾端,并从队列起始选一个节点,从这继续搜索。借由总是把较深的节点放在队列尾端,我们确保网络一次被搜索一层。
图 3.12 中的代码较不复杂地表示这个概念。我们不仅想要找到节点,还想保有我们怎么到那的纪录。所以与其维护一个具有节点的队列 (queue),我们维护一个已知路径的队列,每个已知路径都是一列节点。当我们从队列取出一个元素继续搜索时,它是一个含有队列前端节点的列表,而不只是一个节点而已。
函数 bfs 负责搜索。起初队列只有一个元素,一个表示从起点开始的路径。所以 shortest-path 调用 bfs ,并传入 (list (list start)) 作为初始队列。
bfs 函数第一件要考虑的事是,是否还有节点需要探索。如果队列为空, bfs 返回 nil 指出没有找到路径。如果还有节点需要搜索, bfs 检查队列前端的节点。如果节点的 car 部分是我们要找的节点,我们返回这个找到的路径,并且为了可读性的原因我们反转它。如果我们没有找到我们要找的节点,它有可能在现在节点之后,所以我们把它的子节点(或是每一个子路径)加入队列尾端。然后我们递回地调用 bfs 来继续搜寻剩下的队列。
因为 bfs 广度优先地搜索,第一个找到的路径会是最短的,或是最短之一:
CL-USER> (shortest-path 'a 'd min)
(A C D)
这是队列在我们连续调用 bfs 看起来的样子:
((A))
((B A) (C A))
((C A) (C B A))
((C B A) (D C A))
((D C A) (D C B A))
在队列中的第二个元素变成下一个队列的第一个元素。队列的第一个元素变成下一个队列尾端元素的 cdr 部分。
在图 3.12 的代码不是搜索一个网络最快的方法,但它给出了列表具有多功能的概念。在这个简单的程序中,我们用三种不同的方式使用了列表:我们使用一个符号的列表来表示路径,一个路径的列表来表示在广度优先搜索中的队列 [4] ,以及一个关联列表来表示网络本身。
3.16 垃圾 (Garbages)
有很多原因可以使列表变慢。列表提供了顺序存取而不是随机存取,所以列表取出一个指定的元素比数组慢,同样的原因,录音带取出某些东西比在光盘上慢。电脑内部里, Cons 对象倾向于用指针表示,所以走访一个列表意味着走访一系列的指针,而不是简单地像数组一样增加索引值。但这两个所花的代价与配置及回收Cons 核 (cons cells)比起来小多了。
自动内存管理(Automatic memory management)是 Lisp 最有价值的特色之一。 Lisp 系统维护着一段內存称之为堆(Heap)。系统持续追踪堆当中没有使用的内存,把这些内存发放给新产生的对象。举例来说,函数 cons ,返回一个新配置的 Cons 对象。从堆中配置内存有时候通称为 consing 。
如果内存永远没有释放, Lisp 会因为创建新对象把内存用完,而必须要关闭。所以系统必须周期性地通过搜索堆 (heap),寻找不需要再使用的内存。不需要再使用的内存称之为垃圾 (garbage),而清除垃圾的动作称为垃圾回收 (garbage collection或 GC)。
垃圾是从哪来的?让我们来创造一些垃圾:
CL-USER> (setf lst (list 'a 'b 'c))
(A B C)
CL-USER> (setf lst nil)
NIL
一开始我们调用 list , list 调用 cons ,在堆上配置了一个新的 Cons 对象。在这个情况我们创出三个 Cons 对象。之后当我们把 lst 设为 nil ,我们没有任何方法可以再存取 lst 列表 (a b c) 。
因为我们没有任何方法再存取列表,它也有可能是不存在的。我们不再有任何方式可以存取的对象叫做垃圾。系统可以安全地重新使用这三个 Cons 核。
这种管理內存的方法,给程序员带来极大的便利性。你不用显式地配置 (allocate)或释放 (dellocate)內存。这也表示了你不需要处理因为这么做而可能产生的臭虫。內存泄漏 (Memory leaks)以及迷途指针 (dangling pointer)在 Lisp 中根本不可能发生。
但是像任何的科技进步,如果你不小心的话,自动內存管理也有可能对你不利。使用及回收堆所带来的代价有时可以看做 cons 的代价。这是有理的,除非一个程序从来不丢弃任何东西,不然所有的 Cons 对象终究要变成垃圾。 Consing 的问题是,配置空间与清除內存,与程序的常规运作比起来花费昂贵。近期的研究提出了大幅改善內存回收的演算法,但是 consing 总是需要代价的,在某些现有的 Lisp 系统中,代价是昂贵的。
除非你很小心,不然很容易写出过度显式创建 cons 对象的程序。举例来说, remove 需要复制所有的 cons 核,直到最后一个元素从列表中移除。你可以借由使用破坏性的函数避免某些 consing,它试着去重用列表的结构作为参数传给它们。破坏性函数会在 12.4 节讨论。
当写出 cons 很多的程序是如此简单时,我们还是可以写出不使用 cons 的程序。典型的方法是写出一个纯函数风格,使用很多列表的第一版程序。当程序进化时,你可以在代码的关键部分使用破坏性函数以及/或别种数据结构。但这很难给出通用的建议,因为有些 Lisp 实现,內存管理处理得相当好,以致于使用 cons有时比不使用 cons 还快。这整个议题在 13.4 做更进一步的细部讨论。
无论如何 consing 在原型跟实验时是好的。而且如果你利用了列表给你带来的灵活性,你有较高的可能写出后期可存活下来的程序。
Chapter 3 总结 (Summary)
1)一个 Cons 是一个含两部分的数据结构。列表用链结在一起的 Cons 组成。
2)判断式 equal 比 eql 来得不严谨。基本上,如果传入参数印出来的值一样时,返回真。
3)所有 Lisp 对象表现得像指针。你永远不需要显式操作指针。
4)你可以使用 copy-list 复制列表,并使用 append 来连接它们的元素。
5)游程编码是一个餐厅中使用的简单压缩演算法。
6)Common Lisp 有由 car 与 cdr 定义的多种存取函数。
7)映射函数将函数应用至逐项的元素,或逐项的列表尾端。
8)嵌套列表的操作有时被考虑为树的操作。
9)要判断一个递归函数是否正确,你只需要考虑是否包含了所有情况。
10)列表可以用来表示集合。数个内置函数把列表当作集合。
11)关键字参数是选择性的,并不是由位置所识别,是用符号前面的特殊标签来识别。
12)列表是序列的子类型。 Common Lisp 有大量的序列函数。
13)一个不是正规列表的 Cons 称之为点状列表。
14)用 cons 对象作为元素的列表,可以拿来表示对应关系。这样的列表称为关联列表(assoc-lists)。
15)自动内存管理拯救你处理内存配置的烦恼,但制造过多的垃圾会使程序变慢。
笔记:
一、常用函数函数
1)consp:如果参数是一个 Cons 对象,函数 consp 返回真
2)copy-list: 接受一个列表,然后返回此列表的复本。新的列表会有同样的元素,但是装在新的 Cons 对象里
3)append:函数 append 返回任何数目的列表串接 (concatenation)
4)nth: 找到列表特定位置的元素
5)nthcdr:找到第 n 个 cdr
nth 与 nthcdr 都是零索引的 (zero-indexed); 即元素从 0 开始编号,而不是从 1 开始。在 Common Lisp 里,无论何时你使用一个数字来参照一个数据结构中的元素时,都是从 0 开始编号的。
6)zerop:仅在参数为零时,才返回真
7)last:返回列表的最后一个 Cons 对象
Common Lisp 定义了函数 first 直到 tenth 可以取得列表对应的元素。这些函数不是 零索引的 (zero-indexed)
8)mapcar:接受一个函数以及一个或多个列表,并返回把函数应用至每个列表的元素的结果,直到有的列表没有元素为止
9)maplist:相关的 maplist 接受同样的参数,将列表的渐进的下一个 cdr 传入函数
10)atom:原子 (atom)判断式
11)copy-tree:接受一个树,并返回一份副本
12)substitute:替换序列 (sequence)中的元素
13)subst:替换树之中的元素
14)adjoin:函数 adjoin 像是条件式的 cons 。它接受一个对象及一个列表,如果对象还不是列表的成员,才构造对象至列表上
15)union:并集 (union)
16)intersection:交集 (intersection)
17)set-difference:补集 (complement)
18)length:返回序列中元素的数目
19)subseq:复制序列的一部分。第二个(需要的)参数是第一个开始引用进来的元素位置,第三个(选择性)参数是第一个不引用进来的元素位置。
20)reverse:返回与其参数相同元素的一个序列,但顺序颠倒。
21)sort:排序函数。它接受一个序列及一个比较两个参数的函数,返回一个有同样元素的序列,根据比较函数来排序
22)every: 接受一个判断式及一个或多个序列。当我们仅输入一个序列时,它们测试序列元素是否满足判断式
23)some: 接受一个判断式及一个或多个序列。当我们仅输入一个序列时,它们测试序列元素是否满足判断式
24)push:(push x y)把 x 放入列表 y 的前端。
25)pop:(pop x) 则是将列表 x 的第一个元素移除,并返回这个元素
26)pushnew:pushnew 宏是 push 的变种,使用了 adjoin 而不是 cons
27)assoc:取出在关联列表中,与给定的键值有关联的 Cons 对
二、操作符(好像也可以叫函数)
1)equal:本质上 equal 若它的参数打印出的值相同时,返回真