今天来整理一下查找。
什么是查找?
其实我真的不想解释,嘻嘻,好吧。
来个官方一点的解释吧:
查找(searching)是这样一个过程,即在某个项目组中寻找某一指定目标元素,或者确定该组中并不存在该目标元素。 -from 《Java软件结构与数据结构》
其实通俗点说就是看有没有。真的好通俗!
有哪些查找方式?
一般常见的就两个:
- 线性查找
- 二分查找
来,我们一个一个来看。这里,为了简化问题,我们以整型数组作为我们要查找的序列。
好,开始!
线性查找 (linear search)
从名字中的“线性”我们大概能猜出来这种查找方式是怎么回事,线性嘛!一个一个找嘛!来直接看图:
看到没,线性查找就是从数组的起始位置a[0]开始 依次比较数组中的每一个值直到找到目标值,当然也有可能循环遍历了数组中所有值也没找到目标值。
下面我用代码来演示这一过程:
public class LinearSearchDemo {
public static void main(String[] args) {
int[] data = {2, 1, 4, 6, 12, 7};
int target = 12;
int searchIndex = search(data, target);
if (searchIndex != -1) {
System.out.println("found at: " + searchIndex);
}else {
System.out.println("not found");
}
}
/*
*@param data 待查找的数组
*@param target 待查找的值
*@return int 目标值在数组中的索引,如果没找到返回-1
*/
public static int search(int[] data, int target) {
int length = data.length;
//从头遍历数组中的各个值,如果找到目标值就返回其索引
for (int i = 0; i < length; i++) {
if (data[i] == target) {
return i;
}
}
//代码能走到这一步就说明上面的循环遍历结束了也没找到目标值
//即目标值不存在于数组中
return -1;
}
}
输出结果:
found at: 4
线性查找的效率当然不是很高效,最坏情况是数组中没有我们要找的目标值,但是我们还是要遍历完整个数组才能知道。但是它的优点就是很简单,特别的简单,而且它还不要求待查找的数组是有序的。下面将要介绍的二分查找效率上要比线性查找高,但是它要求待查找的数组中的数据必须是有序的,我们接着来看。
二分查找( binary search)
先来个比较官方的解释:
二分搜索(英语:binary search),也称折半搜索(英语:half-interval search)、对数搜索(英语:logarithmic search),是一种在有序数组中查找某一特定元素的搜索算法。 搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的 那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。 - from 维基百科
以上介绍参考自维基百科(PS:非常建议大家多上Google,多上Wikipedia,相信我,你会爱上它们的,哈哈~)
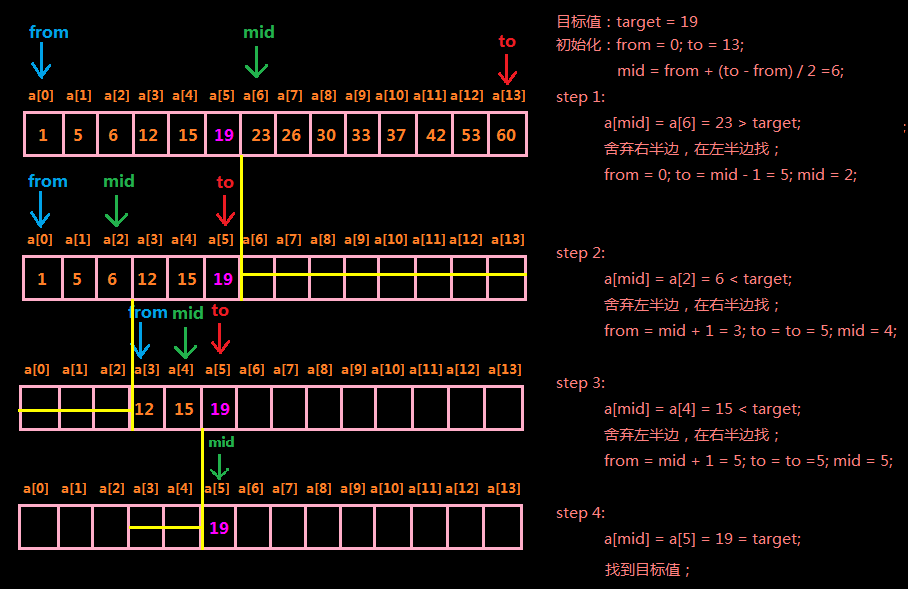
好,看完比较正式的解释如果不太理解,没关系,拿图来说话:
二分法首先考察中间元素a[mid],如果该值是我们要找的值,那好极了,直接找到了;如果不是的话,由于我们已经知道数组是排好序的(二分法要求待查找的数组是有序的,本例假设是升序的,降序其实是一样的),那就看目标值target和a[mid]的关系是怎样的:如果a[mid] > target则说明目标值target如果存在的话一定在a[mid]的左侧,因为左侧都比a[mid]小;如果a[mid] < target则说明目标值如果存在的话一定在a[mid]的右侧,因为右侧都比a[mid]大。
因为a[mid]处在数组的中间位置,所以它的左侧或者右侧都是数组的一半,这样每一次我们通过a[mid]和target的比较就可以排除掉一半的数据。最后只有两种情况,要么我们找到了目标值,要么我们排除了所有数据没有找到目标值。
由此看来,在处理已排序数据的查找工作时,二分查找法显然效率高于线性查找法。这种优势在数据量越大的时候越明显。
比如说,现在有序数组中含有100万个数据,我们要求查找特定元素。如果使用线性查找法,我们必须对这一100万个数据依次考察以确定出目标元素是不是存在,最好的情况是目标元素在数组的第一个位置a[0],这样只要一次就查找到目标元素了,最坏情况是目标元素在数组的最后a[999999],这样我们就得比较100万次才能知道目标元素到底在不在,平均下来看的话也需要50万次比较。而如果使用二分查找法,我们大约做20次比较就可以知道目标元素是不是存在于数组中了。
50万 VS 20!
是不是很惊悚?为了达到目的我们可以使用不同的算法,但是这些算法之间的差异真的很大! 在数据量越大的时候二分法的优势越明显。
以下是我用Java代码实现的,有递归的和非递归两种方式。代码注释都写的很清楚,相信大家对照着上面我的介绍应该可以看得懂哈~
//二分查找:在有序数组中查找某一特定元素的搜索算法
public class BinarySearch {
public static void main(String[] args) {
int[] data = {1, 5, 6, 12, 15, 19, 23, 26, 30, 33, 37, 42, 53, 60};
int target = 19;
int index = binarySearch2(data, 0, data.length - 1, target);
if (index > -1) {
System.out.println("found :" + index);
}else {
System.out.println("not found");
}
}
/**
* 递归方法实现二分查找
* @param data 已排序数组(这里假设是从小到大排序)
* @param from 起始位置
* @param to 终止位置
* @param target 要查找的值
* @return 要查找的值在数组中的位置,如果没找到则返回-1
*/
private static int binarySearch1(int[] data, int from, int to, int target) {
if (from <= to) {
int mid = from + (to - from) / 2;//中间位置,为了防止溢出使用这种方式求中间位置
if (data[mid] < target) {//中间的值比目标值小,则在左半边继续查找
return binarySearch1(data, mid + 1, to, target);
}else if(data[mid] > target){//中间的值比目标值大,则在右半边继续查找
return binarySearch1(data, from, mid - 1, target);
}else {//找到了,把找到的情况放在最后是因为多数情况下中间值不是大于就是小于,这样做可以节省操作
return mid;
}
}
return -1;
}
/**
* 非递归方法实现二分查找
* @param data 已排序数组(这里假设是从小到大排序)
* @param from 起始位置
* @param to 终止位置
* @param target 要查找的值
* @return 要查找的值在数组中的位置,如果没找到则返回-1
*/
private static int binarySearch2(int[] data, int from, int to, int target) {
while(from <= to) {
int mid = from + (to - from) / 2;
if (data[mid] < target) {
from = mid + 1;
}else if(data[mid] > target) {
to = mid - 1;
}else {//找到了,把找到的情况放在最后是因为多数情况下中间值不是大于就是小于,这样做可以节省操作
return mid;
}
}
return -1;
}
}
打印结果:
found: 5
到这里,文章差不多要结束了,最后我们再想一个问题,就是既然二分查找法效率这么高,甩线性查找法好多条街,那为什么还要线性查找法呢?
其实,线性查找法也不是一无是处,它最大的优点就是简单,特别简单,傻瓜式的。你不是让我找东西吗,好啊,那我就把我兜里所有的东西一个一个拿出来看看有没有,是不是很傻瓜式哈~
还有一点就是二分法本身也有局限性,那就是二分法必须要求待查数组是已排序的,比如我给你一个很大的数组,但是这个数组并没有排序,那你如果想用二分查找法的话还必须先给数组排序,然后再查找。这样就会造成除查找之外的额外成本(排序),至于这个额外成本是不是可承受的,就要看设计者自己权衡了,搞不好还不如人家线性查找快呢,嘿嘿~
好了,谢谢观看~