前提摘要
从2000年风靡全球的war3,星际争霸,到现在可能入围奥林匹克奥运比赛项目的LOL。我相信绝大部分的人对这些应该都不陌生,甚至绝大部分的都有接触。不知道大家在体验激情四射的游戏时有没有注意到我们的左下角有一个迷你地图 我们鼠标点在迷你地图的一个坐标上,我们所控制的角色就会自动按照最短的路径去我们所点的目的地。我们不去细想时觉得这是理所当然,但是当我们仔细去注意我们所控制的人物每次都能按照最短的路径去到达终点是不是又会有一点感到很神奇呢?
这就好比我们的角色身处一个迷宫之中,我们只要点击出口位置一下他们就会自动按照最短最优的路径走出迷宫而且不会发生碰壁。是不是感到很惊讶!没错这就是我们今天需要引出的知识:深度优先搜索。-
何为深度优先搜索?
深度优先搜索属于图算法的一种,英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。-
举例说明之:下图是一个无向图,如果我们从A点发起深度优先搜索(以下的访问次序并不是唯一的,第二个点既可以是B也可以是C,D),则我们可能得到如下的一个访问过程:A->B->E(没有路了!
回溯到A)->C->F->H->G->D(没有路,最终回溯到A,A也没有未访问的相邻
节点,本次搜索结束).简要说明深度优先搜索的特点:每次深度优先搜索的结果必然是图的一个连通分量.深度优先搜索可以从多点发起.如果将每个节点在深度优先搜索过程中的"结束时间"排序(具体做法是创建一个list,然后在每个节点的相邻节点都已被访问的情况下,将该节点加入list结尾,然后逆转整个链表),则我们可以得到所谓的"拓扑排序",即topological sort。
[ 理解深度优先搜索的关键在于当下应该怎么做,至于下一步应该怎么做和前面那一步是相同的。
-
-
实例
如果当你不理解某个问题时,用实例来明白我认为是最合适不过了。
-
如果就是给我们一张这样的图片,让我们最快的时间把喊救命的人救出来,你该如何做?
- 考察点①:如何将现实中的事情模型化。
- 考察点②:如何运用我们所知道的知识将模型支撑起来。
分析:上面的图片由4*5的格子组成 格子中有的地方是不能走。那么我们能不能把图片上的事物以二维数组的形式展现出来。这样我们要在最快的时间内把人救出的问题就可以转变成在如何走最少的格子到达喊救命的人的地方。这样问题就简化成在二维数组构成的图中如何走最少的格子到达目的地。以二维数组表示这个图就是如下这样了。
- 这里有几个需要注意的地方
-
我们走的每一步都是独立的。也就是说我们每一步都有四种可能,我们可以往上下左右四个方向都可以。
我们用二维数组的方式去表示图的时候我们要注意下标越界的问题。
控制不走回头路(就是已经走过的路径在这次中不能在走。)
说白了深度优先搜索就是一遍一遍的去尝试,当遇到走不通的时候退回上一步往另外一个方向尝试,如果另外的方向可以走就去另外的方向继续尝试,如果这一步所有的方向都走不通的时候,就在退回的上上步就这样一次一次的循环下去直到到达目的地。(当然这里还要统计走的是不是最短的路径如果不是就还是需要继续尝试下去直到所有的地方都尝试完才结束)
-
语文水平实在有限~~~,还是上代码详解:
package javasort;
/**迷宫解密之深度优化搜索*/
/*
* 迷宫解密也可以称为迷宫最短路径路线问题
* 这也是一个深度优化搜索的案例应用场景 在游戏之中也很常见这种算法比如现在比较活的游戏lol中点击
* 小地图,我们的角色就会按照那条计算出来的最短路径前进。这其中就涉及到深度优化搜索的身影。
* 一般我们采用这种方法,我们都应该事先建立一个与之相对应的模型,如果是图,我们可以建立一个
* 类似于二维数组一样的模型与之对应。
* 现在我们需要解决的问题是如果一个人在一个点去另外一个点的最短路径的问题 并计算出最短路径
* 我们定义的模型如下:采用二维数组
* {[0,0,1,0],
* [0,0,0,0],
* [0,0,1,0],
* [0,1,0,0],
* [0,0,0,1]}
* 其中0代表可以走的地方 1代表不能走的地方
* (x,y) x代表行 y代表列
* (0,0)坐标是我们的起点
* (3,2) 代表目的地
* 求出到达目的地的最短路径(注意一次只能走一步 上下左右 但是不能越界)
* */
public class MazeDecode {
// 定义一个参照数组 相当于记录所走的地方
private static int[][] book = new int[5][4];
// 定义地图 初始化地图
private static int[][] a = {{0,0,1,0},
{0,0,0,0},
{0,0,1,0},
{0,1,0,0},
{0,0,0,1}};
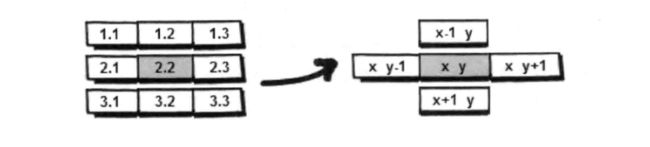
// 定义四个方向 上下左右 上=x-1,y不变 下=x+1,y不变 左=x不变,y-1 右=x不变,y+1
// 根据这个特性我们可以将这四个方向定义成一个二维数组
private static int[][] direction = {{-1,0},{1,0},{0,1},{0,-1}};
// 定义一个走的步数
private static int stepSum = 9999;
/**这是每一次走的函数*/
//x y 相等于 行和列 因为数组是从0开始的所以xy也是从0开始
public static void dfs(int tx, int ty,int step){
//System.out.println(tx +":"+ty+":"+step);
// x,y 这里表示xy点已经被走过了所以需要标记
// book[tx][ty] = 1;
// 如果到达了目的地就需要return
if(tx==3 && ty==2){
// 表示到达目的地 这里还需要记录所走的步数
if(step < stepSum){
stepSum = step;
}
// 将所走的路径遍历出来 也就是book二维数组中等于1的
for(int m=0;m<5;m++){
for(int n=0;n<4;n++){
if(book[m][n] == 1){
System.out.print("("+m+","+n+")");
}
}
}
System.out.print("步数是:"+step);
System.out.println();
return;
}
// 因为每一步都有四种走法
for(int i=0;i=0 && x<5 && y>=0 && y <4 && a[x][y] == 0 && book[x][y] == 0){
book[x][y] = 1;
dfs(x,y,step+1);
//step--;
// 这一步很重要 相当于走了一趟之后重新走的时候撤掉标记
book[x][y] = 0;
}
}
//return;
}
public static void main(String[] args) {
book[0][0]=1;
dfs(0,0,0);
}
}
总结
- 所谓深度优先搜索的核心思想是:解决当下该如何做,至于后面的和前一步是一样的 只是无聊的递归下去。
- 把握越界的几个零界点。(横轴方向,竖轴方向,到达目的地点)
- 事先定义一个和数组一样大的一个空数组,用来记录经过了那些点(标记)。这样做的目的是不走已经走过的点。
- 如果是返回上一步的时候,要将标记取消这一步是这里代码的精华之处。为什么要取消标记?因为如果前面的尝试已经结束了 返回上一步,如果不把标记取消那么后面就没法继续尝试。()