绘制图表的重要性——基于Python从安斯库姆四重奏到等候排队理论的研究

Anscombe's quartert, variability and studying queues with Python - 从安斯库姆四重奏到等候排队理论的研究

Anscombe’s quartet - 安斯库姆四重奏 是四组基本的统计特性一致的数据，但它们的分布却非常不同。

性质	数值
x的平均数	9
x的方差	11
y的平均数	7.50（精确到小数点后两位）
y的方差	4.122或4.127（精确到小数点后三位）
x与y之间的相关系数	0.816（精确到小数点后三位）
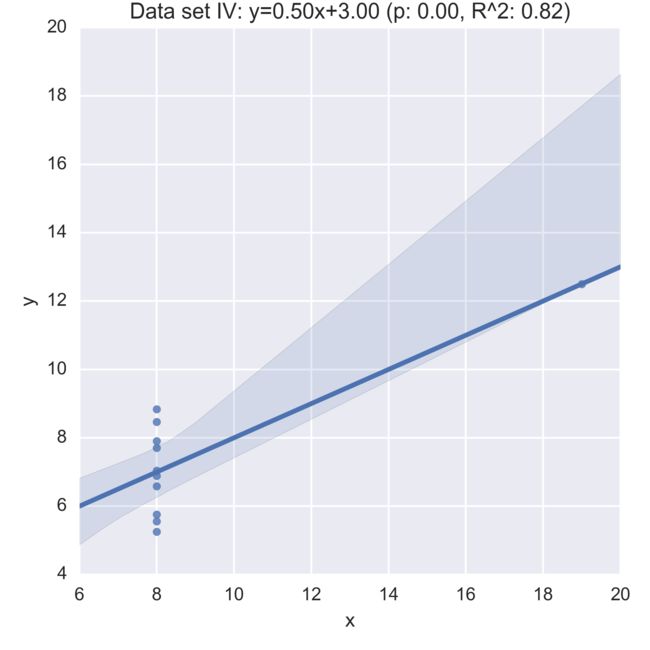
线性回归线	y=3.00+0.500x（分别精确到小数点后两位和三位）

让我们使用Python和seaborn库、Ciw库 etc. 来探索一下吧

---

引入库

import pandas as pd  # Data manipulation
import ciw  # The discrete event simulation library we will use to study queues
import matplotlib.pyplot as plt  # Plots
import seaborn as sns  # Powerful plots
from scipy import stats  # Linear regression
import numpy as np  # Quick summary statistics
import tqdm  # A progress bar

缺少相应库使用pip install即可

加载Anscombe数据集

anscombe = sns.load_dataset("anscombe")

我们得到四组数据集，每组由11个(x, y)点构成：

   dataset     x      y
0        I  10.0   8.04
1        I   8.0   6.95
2        I  13.0   7.58
3        I   9.0   8.81
4        I  11.0   8.33
5        I  14.0   9.96
6        I   6.0   7.24
7        I   4.0   4.26
8        I  12.0  10.84
9        I   7.0   4.82
10       I   5.0   5.68
11      II  10.0   9.14
12      II   8.0   8.14
13      II  13.0   8.74
14      II   9.0   8.77
15      II  11.0   9.26
16      II  14.0   8.10
17      II   6.0   6.13
18      II   4.0   3.10
19      II  12.0   9.13
20      II   7.0   7.26
21      II   5.0   4.74
22     III  10.0   7.46
23     III   8.0   6.77
24     III  13.0  12.74
25     III   9.0   7.11
26     III  11.0   7.81
27     III  14.0   8.84
28     III   6.0   6.08
29     III   4.0   5.39
30     III  12.0   8.15
31     III   7.0   6.42
32     III   5.0   5.73
33      IV   8.0   6.58
34      IV   8.0   5.76
35      IV   8.0   7.71
36      IV   8.0   8.84
37      IV   8.0   8.47
38      IV   8.0   7.04
39      IV   8.0   5.25
40      IV  19.0  12.50
41      IV   8.0   5.56
42      IV   8.0   7.91
43      IV   8.0   6.89

查看统计数据

anscombe.groupby("dataset").describe()

得到非常相近的结果

                       x          y
dataset                            
I       count  11.000000  11.000000
        mean    9.000000   7.500909
        std     3.316625   2.031568
        min     4.000000   4.260000
        25%     6.500000   6.315000
        50%     9.000000   7.580000
        75%    11.500000   8.570000
        max    14.000000  10.840000
II      count  11.000000  11.000000
        mean    9.000000   7.500909
        std     3.316625   2.031657
        min     4.000000   3.100000
        25%     6.500000   6.695000
        50%     9.000000   8.140000
        75%    11.500000   8.950000
        max    14.000000   9.260000
III     count  11.000000  11.000000
        mean    9.000000   7.500000
        std     3.316625   2.030424
        min     4.000000   5.390000
        25%     6.500000   6.250000
        50%     9.000000   7.110000
        75%    11.500000   7.980000
        max    14.000000  12.740000
IV      count  11.000000  11.000000
        mean    9.000000   7.500909
        std     3.316625   2.030579
        min     8.000000   5.250000
        25%     8.000000   6.170000
        50%     8.000000   7.040000
        75%     8.000000   8.190000
        max    19.000000  12.500000

计算回归曲线

for data_set in anscombe.dataset.unique():  # array(['I', 'II', 'III', 'IV'], dtype=object)
    df = anscombe.query("dataset == '{}'".format(data_set))
    slope, intercept, r_val, p_val, slope_std_error = stats.linregress(x=df.x, y=df.y)
    sns.lmplot(x="x", y="y", data=df);
    plt.title("Data set {}: y={:.2f}x+{:.2f} (p: {:.2f}, R^2: {:.2f})".format(data_set, slope, intercept, p_val, r_val))

虽然数据分布十分不一样，但是它们的线性回归却惊人的一致。

分析

上面的事实经常被用来证明一个数据集的统计信息会固有地丢失数据信息，因此应该伴随着进一步的研究/理解（例如在这种情况下：查看数据的图）。
参考： Generating Data with Identical Statistics but Dissimilar Graphics: A Follow up to the Anscombe Dataset

引申

在Queueing theory - 等候理論中，理解类似上文的变异性是非常必要的。
我之前的一篇博文calculating the expected wait in a tandem queue（计算串联队列中的预期等待）讲解了队列理论。其中，主要想法是假定在排队系统中个体到达的间隔时间的某一（随机）分布和为服务每个个体所花费的时间的另一（随机）分布。
在分析上这些会被当作Markov chain - 马尔可夫链研究。单个服务器队列的维基百科条目展示了相应链的图片。
队列的马尔科夫模型假定了（到达时间间隔和服务时间的）分布是马尔可夫的：即指数分布。这通常是一个很好地模拟现实情况的分布，但它也常是不现实的。例如在医疗系统中，诸如医院病房（就是队列），服务时间分布通常遵循Log-normal distribution - 对数正态分布。
当学习队列以及建立分析模型时，可以使用伪随机数发生器来模拟过程。一个用于这个研究的小软件就是ciw（主要开发者是Geraint Palmer-phd在读，Paul Harper和我）。
下面将使用ciw模拟一个单个服务器队列的模型，其中个体到达平均速率为0.5每时间单位（即到达之间有2个时间单位），并且平均以每时间单位1的速率提供服务（即每次服务为1个时间单位）。
我们需要在ciw中构建一个参数字典。Ciw被编写为便于处理大多数排队系统，但是特别考虑到排队网络，也考虑到了处理多个类别的个体的能力。在下面的系统中，我们只有一个个体类Class 0，转换矩阵会显得有点冗余，因为我们只处理单个队列。这里是我们的系统在假设指数分布时的字典：

parameters = {'Arrival_distributions': {'Class 0': [['Exponential', 0.5]]},
              'Service_distributions': {'Class 0': [['Exponential', 1]]},
              'Transition_matrices': {'Class 0': [[0.0]]},
              'Number_of_servers': [1]}

这里是运行单个模拟的函数：

def iteration(parameters, maxtime=250, warmup=50):
    """
    Run a single iteration of the simulation and
    return the times spent waiting for service
    as well as the service times
    """
    N = ciw.create_network(parameters)
    Q = ciw.Simulation(N)
    Q.simulate_until_max_time(maxtime)
    records = [r for r in  Q.get_all_records() if r.arrival_date > warmup]
    waits = [r.waiting_time for r in records]
    service_times = [r.service_time for r in records]
    n = len(waits)
    return waits, service_times

下面是多次运行模拟组合成的一个实验函数，它对于帮助平滑随机过程的随机性是很重要的。

def trials(parameters, repetitions=30, maxtime=2000, warmup=250):
    """Repeat out simulation over a number of trials"""
    waits = []
    service_times = []
    for seed in tqdm.trange(repetitions):  # tqdm gives us a nice progress bar
        ciw.seed(seed)
        wait, service_time = iteration(parameters, maxtime=maxtime, warmup=warmup)
        waits.extend(wait)
        service_times.extend(service_time)
    return waits, service_times

让我们以默认参数运行实验：

waits, service_times = trials(parameters)

首先，让我们验证预期的服务时间（回想下应该是1个时间单位）：

np.mean(service_times)
# 输出 1.0024931747410142

我们还可以检查平均等待是否和理论值一致，理论值为ρ/[μ(1−ρ)]，其中ρ=λ/μ，with λ，μ being the interarrival and service rates

lmbda = parameters['Arrival_distributions']['Class 0'][0][1]
mu = parameters['Service_distributions']['Class 0'][0][1]
rho = lmbda / mu
np.mean(waits), rho / (mu * (1 - rho))
# 输出 (1.0299693832838621, 1.0)

既然我们已经实现了一个简单的马尔科夫系统，让我们创建一些具有相同平均服务时间的分布并比较它们：

distributions = [
    ['Uniform', 0, 2],  # A uniform distribution with mean 1
    ['Deterministic', 1],  # A deterministic distribution with mean 1
    ['Triangular', 0, 2, 1],  # A triangular distribution with mean 1
    ['Exponential', 1],  # The Markovian distribution with mean 1
    ['Gamma', 0.91, 1.1], # A Gamma distribution with mean 1
    ['Lognormal', 0, .1], # A lognormal distribution with mean 1
    ['Weibull', 1.1, 3.9],  # A Weibull distribuion with mean 1
    ['Empirical', [0] * 19 + [20]]  # An empirical distribution with mean 1 (95% of the time: 0, 5% of the time: 20)
   ]

（更多信息从ciw关于分布的文档中获得）

利用trials函数模拟上述所有分布的排队过程：

columns = ["distribution", "waits", "service_times"]
df = pd.DataFrame(columns=columns)  # Create a dataframe that will keep all the data
for distribution in distributions:
    parameters['Service_distributions']['Class 0'] = [distribution]
    waits, service_times = trials(parameters)
    n = len(waits)
    df = df.append(pd.DataFrame(list(zip([distribution[0]] * n, waits, service_times)), columns=columns))

分析下面的统计数据，我们看到所有分布具有相同的平均服务时间，但平均等待时间却截然不同：

bydistribution = df.groupby("distribution")  # Grouping the data
for name, df in sorted(bydistribution, key= lambda dist: dist[1].waits.max()):
    print("{}:\n\t Mean service time: {:.02f}\n\t Mean waiting time: {:.02f}\n\t 95% waiting time: {:.02f} \n\t Max waiting time: {:.02f}\n".format(
                                                        name,
                                                        df.service_times.mean(),
                                                        df.waits.mean(),
                                                        df.waits.quantile(0.95),
                                                        df.waits.max()))

输出统计数据

Deterministic:
         Mean service time: 1.00
         Mean waiting time: 0.51
         95% waiting time: 2.11 
         Max waiting time: 6.73

Weibull:
         Mean service time: 1.00
         Mean waiting time: 0.54
         95% waiting time: 2.24 
         Max waiting time: 8.16

Lognormal:
         Mean service time: 1.01
         Mean waiting time: 0.51
         95% waiting time: 2.09 
         Max waiting time: 8.53

Triangular:
         Mean service time: 1.00
         Mean waiting time: 0.59
         95% waiting time: 2.48 
         Max waiting time: 9.21

Uniform:
         Mean service time: 1.00
         Mean waiting time: 0.67
         95% waiting time: 2.84 
         Max waiting time: 10.42

Exponential:
         Mean service time: 1.00
         Mean waiting time: 1.03
         95% waiting time: 4.76 
         Max waiting time: 16.41

Gamma:
         Mean service time: 1.00
         Mean waiting time: 1.02
         95% waiting time: 4.72 
         Max waiting time: 20.65

Empirical:
         Mean service time: 0.99
         Mean waiting time: 9.30
         95% waiting time: 37.60 
         Max waiting time: 100.60

例如，经验分布中至少有一个个体的等待时间超过了100个时间单位！（要记得，平均每2个时间单位到达一个个体，并且个体平均被服务1个时间单位！）还有5%的个体在经验分布中等待了超过37个时间单位，以及更保守的分布中5%的个体等待时间超过：4.72个时间单位（Gamma），4.76个时间单位（Exponential），2.84时间单位（Uniform） ...
但是正如我们一开始提到的，就像看安斯库姆四重奏那样，重要的是不要仅看统计信息，所以让我们看图：

for name, df in sorted(bydistribution, key= lambda dist: dist[1].waits.max())[:-1]:
    plt.hist(df.waits, normed=True, bins=20, cumulative=True,
             histtype = 'step', label=name, linewidth=1.5)
plt.title("Cdf (excluding the empirical distribution)")
plt.xlabel("Waiting time")
plt.ylabel("Probability")
plt.ylim(0, 1)
plt.legend(loc=5)

for name, df in sorted(bydistribution, key= lambda dist: dist[1].waits.max()):
    plt.hist(df.waits, normed=True, bins=20, cumulative=True,
             histtype = 'step', label=name, linewidth=1.5)
plt.title("Cdf")
plt.xlabel("Waiting time")
plt.ylabel("Probability")
plt.ylim(0, 1)
plt.legend(loc=5)

我们看到，经验分布到目前为止是尾巴最长的，一些个体的等待时间超过了80个时间单位。虽然这种分布是相当人为的，但是假设某一个特定过程或服务几乎不需要多少时间而在很少的情况下却会花费很多的时间，这是相当现实的。这些例子包括了有时需要非常规程序的医疗保健操作。
所有这一切都是模拟一个相当简单的排队系统（单服务器）但是有了Ciw，研究更复杂的系统也变得简单。

此外

Ciw已经相当完善，并且100%测试覆盖，但是它仍需要你的贡献（任何级别的），如果有意，请看：

• The github repo: github.com/CiwPython/Ciw
• A talk given by Geraint Palmer describing the library and his research so far:
  youtube.com/watch?v=0_sIus0mPSM