原文地址:http://happykai.cn/2018/06/07/MIT-PatternRecognition2/ ,没有系统性的目录之分,容易使知识变成一盘散沙,因此今后将逐步转移至个人博客http://happykai.cn,在个人博客中系统地搭建知识体系。
手机版不支持mathjax,所以公式乱码,如果您使用手机阅读,请到个人博客。
主要是概率论,如果你这部分基础牢固,可以跳过,直接看理论部分。
概率质量函数
概率质量函数(Probability Mass Function)是针对离散值而言的,通常用大写字母P表示。假设某个事
件\omega_{1}发生的概率为P(\omega_{1}),某个事件\omega_{2}发生的概率为P(\omega_{2}),两事件相互独立,则P(\omega_{1})+P(\omega_{2})=1。
概率密度函数
概率密度函数(Probability Desity Function)是针对连续值而言的,通常用小写字母p表示。概率密度函数的在正无穷到负无穷上到积分为1,在某一个区间中的概率用在该区间中的积分来表示。
用数学语言描述就是:
(1)p(\overrightarrow {x}) \geq 0, \forall\ \overrightarrow {x}\in R^n
(2)\int p(\overrightarrow {x})\ d\ \overrightarrow x=1
NOTE:
- \overrightarrow x是一个列向量
任何满足以上两个条件的函数都叫在n为欧几里得空间(Euclidean Space)上的概率密度函数。
比如:
高斯密度函数(Gaussian Density Function or Density Function for Gaussian Distribution)
高斯密度函数的定义为:
p(\overrightarrow x)=\dfrac{1}{(\sqrt{2\pi})^n|\Sigma|^{1/2}}exp\left\{-\dfrac{1}{2}(\overrightarrow x-\overrightarrow \mu)^T\Sigma^{-1}(\overrightarrow x - \overrightarrow \mu)\right\}
NOTE:
可能发现上面那个公式和平时见的公式长得不太一样,其实它是从线性代数的角度写的。
公式中的|\Sigma|代表Determinant of sigma, 也就是\Sigma的行列式,将nxn的矩阵映射成一个标量(既然提到了行列式并且我也有些遗忘,所以一会儿在文末附录里整理一下它的概念)。\Sigma是什么呢?它叫Variance-Covariance Matrix, 也叫Dispersion Matrix,是一个nxn的矩阵,它的逆\Sigma^{-1}也是一个nxn的矩阵。(这里协方差矩阵和矩阵的逆还有矩阵的转置,也要在附录里温习)ok,回归正题,这个determinant of sigma可能是0也可能是负数,但是如果是负数,1/2次方就会很难计算,因为它会得到一个非常复杂的数, 而我们的概率密度函数的第一个条件就是p(\overrightarrow x)\geq0,所以determinant ofsigma必须大于0, 因为即使是等于0,1/0也无法计算。
exp代表e的某次方。
\overrightarrow x:一个n维的向量
\overrightarrow \mu:均值向量,代表分布的均值,也是一个n维的向量(mean vector同样在附录里温习)
因为\overrightarrow x和\overrightarrow \mu都是n维的列向量,所以(\overrightarrow x-\overrightarrow \mu)也是一个n维的列向量,即nx1的矩阵,所以(\overrightarrow x-\overrightarrow \mu)^T是一个n维的行向量, 即1xn的矩阵
所以(\overrightarrow x-\overrightarrow \mu)^T\Sigma^{-1}(\overrightarrow x - \overrightarrow \mu)是一个标量,所以这一项是e的任何大于等于0的次方。
看完这里,请跳到附录,补充Variance-Covariance Matrix和Positive-Definite Matrix 的概念,至于行列式(Determinant)和矩阵的逆以及矩阵的转置,看不看都行。
先验概率
先验概率(Prior Probability)是指根据已有情况提前知道的概率,比如已知有一箱红黑混合的小球,其中红色小球共有100颗,黑色小球共有200颗,则红色小球的先验概率为P(red) = 1/3, 黑色小球的鲜艳概率为P(black) = 2/3。
条件概率
假设将上述红黑混合的小球们放在两个箱子中,即A箱放20个红色小球,100个黑色小球,B箱放80个红色小球,100个黑色小球,则从A中取到红色小球的概率是多少?这就是条件概率。
P(red|A) = P(red \& A) / P(A) = (20 / 300) / (120 / 300) = 1/6
那么,红色里面来自A的概率是多少呢?
P(A|red) = P(A \& red) / P(red) = (20 / 300) / (100 / 300) = 1 / 5
附录
Variance-Covariance Matrix
首先需要知道Variance和Covariance的定义。
Variance
假设有n个observations:x_1, x_2, x_3, ..., x_n \in R
它们的平均数\bar x等于:
\bar x=\dfrac {1}{n}\sum_{i=1}^{n}x_i
它们的方差Variance等于
Variance=\dfrac {1}{n}\sum_{i=1}^{n}(x_i-\bar x)^2
一些书也会写为:Variance=\dfrac {1}{n-1}\sum_{i=1}^{n}(x_i-\bar x)^2,这实际上是unbias estimate for Variance of the population,与1/n在value上有些差别,这是统计学中比较复杂的一个概念。(老师没有做详细介绍,说可以课后去查,而我也不打算深入此概念,所以和老师一样,variance就follow第一种写法。)
Covariance
为了阐释协方差Covariance,我们需要两个变量(x, y),假设x是身高,单位是cm,y是体重,单位是kg。
假设有n个observations:
(x_1,y_1),(x_2, y_2), ..., (x_n, y_n)
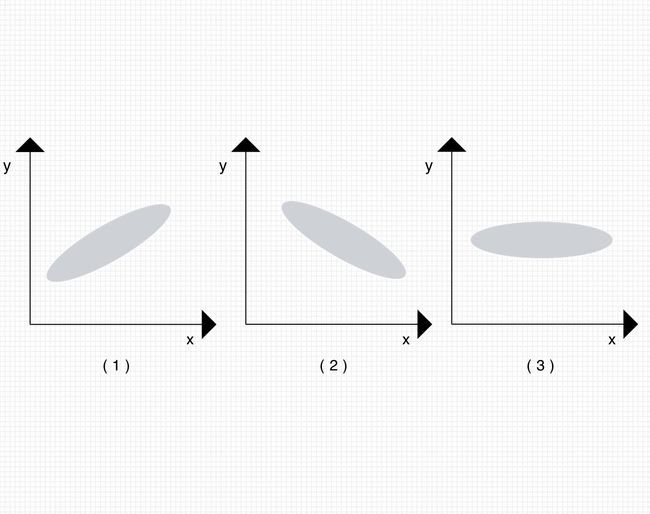
你要做的是plot these points,这里我给出三个这样的plots,灰色区域是一些列点:
图(1)中,x增长,y随x也增长,所以我们用一些大于0的数(quantity)来代表这个关系;
图(2)中,x增长,y随x减小,我们用一些小于0的数(quantity)来代表这个关系;
图(3)中,x增长,y在某一个范围内波动,所以我们用一些非常接近0的数(quantity)来代表这个关系。
那么这个数(quantity)到底是什么呢?
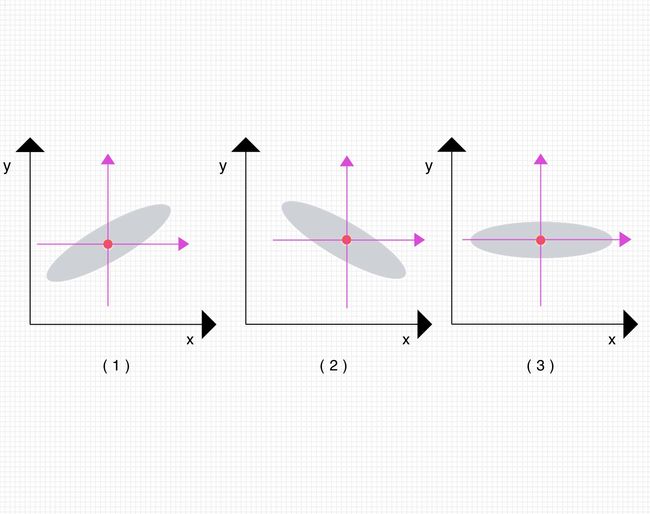
对于所有的x和y,我们找到它们的均值,然后将其作为新坐标轴的原点:
那么所有点的x,y值都会变化,把这些新的值乘起来求均值,会得到什么呢?
比如图(1),新坐标系第一象限的x,y都大于0,乘积也会大于0,第三象限x,y都小于0,乘积也会大于0,第二和第四象限乘积会小于0,但是一三象限的点数量明显大于二四象限的点,所以我们计算
\dfrac{1}{n}\sum_{i=1}^n(x_i - \bar x)(y_i - \bar y)
会得到一个大于0的值。
同理图(2)会得到一个小于0的值,图(3)会得到一个约等于0的值。
这就是x和y的协方差Covariance
Cov(x,y)=\dfrac{1}{n}\sum_{i=1}^n(x_i - \bar x)(y_i - \bar y)
可以看出,Cov(x,x)就是variance。
Variance-Covariance Matrix
在模式识别中,我们把这一系列变量称作features,如果两两组合,会得到多少对呢?n^2对。
如果n个features是
x_1, x_2, x_3, \dots,x_n
则这n个features的Variance-Covariance matrix为:
\Sigma=\begin{bmatrix} {Cov(x_1,x_1)}&{Cov(x_1, x_2)}&{\cdots}&{Cov(x_1, x_n)}\\ {Cov(x_2,x_1)}&{Cov(x_2,x_2)}&{\cdots}&{Cov(x_2,x_n)}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {Cov(x_n,x_1)}&{Cov(x_n,x_2)}&{\cdots}&{Cov(x_n,x_n)}\\ \end{bmatrix}
这是一个对称矩阵symmetric matrix,也是一个正定矩阵Positive-definite matrix,什么是正定矩阵呢,往下看。
Positive-definit matrix
大家应该都知道“欧几里得”距离是什么吧,假设我们有一个列向量\overrightarrow x=[x_1, x_2, \dots,x_n]和一个列向量\overrightarrow y=[y_1, y_2, \dots, y_3],则x和y的欧几里得距离为d(\overrightarrow x, \overrightarrow y)=\sqrt{\sum_{i=1}^n(x_i-y_i)^2}。
现在假设x代表第一个人的feature,y代表第二个人的feature,每个列向量只有两列,分别代表身高和体重。
x的身高和体重分别为160cm和70kg,y的身高和体重分别为158cm和73kg,现在想衡量x和y的距离,如果用上面的欧式距离,就会有些问题,为什么这么说呢?
d(\overrightarrow x, \overrightarrow y)=\sqrt{(160-158)^2+(70-73)^2}=\sqrt{13}
如果同样是这两个人,把身高的单位换成mm,同样的方式计算x和有的距离:
d(\overrightarrow x, \overrightarrow y)=\sqrt{(1600-1580)^2+(70-73)^2}=\sqrt{409}
这是我们不期望得到的结果,相同的两个人,衡量他们的距离,应该无论如何都始终一样,而非仅仅换了单位就出现不同的结果。
所以欧式距离往往是not useful的。
现在让我们移除公式的根号:
d^2(\overrightarrow x, \overrightarrow y)=(x_1-y_1, x_2-y_2)\left(\begin{array}{cccc} 1 & 0 \\ 0 & 1\\ \end{array}\right) \left(\begin{array}{cccc} x_1-y_1 \\ x_2-y_2 \\ \end{array}\right)
这种写法与d(\overrightarrow x, \overrightarrow y)=\sqrt{\sum_{i=1}^2(x_i-y_i)^2}是等价的,一个矩阵与单位矩阵(identity matrix)相乘是不变的。
现在我们对中间对单位矩阵做一些泛化,把它改成\left(\begin{array}{cccc} w_1 & 0 \\ 0 & w_2\\ \end{array}\right),则相应的距离公式变为d(\overrightarrow x, \overrightarrow y)=\sqrt{\sum_{i=1}^2w_i(x_i-y_i)^2},这里的w_i取决于单位,这样就能解决我们的问题:当单位发生改变时,相同的两个人距离不发生改变。这种定义下,如果w_1和w_2严格大于等于0,那么最后的距离就是大于或者等于0的
你还可以继续泛化,把单位矩阵改成\left(\begin{array}{cccc} w_{11} & w_{12} \\ w_{21} & w_{22} \\ \end{array}\right),在这种定义下,w的值该取多少距离才会大于0呢?
满足这样的w有很多,比如随便举个例子:
(x_1-y_1, x_2-y_2)\left(\begin{array}{cccc} 2 & -1 \\ -1 & 2 \\ \end{array}\right)\left(\begin{array}{cccc} x_1-y_1 \\ x_2-y_2\\ \end{array}\right) > 0, \ if(x_1 \neq y_1)\ or\ (x_2 \neq y_2)
这样我们的Positive-definite matrix就有了定义:
A_{n*n} is said to be POSITIVE DEFINITE if a^TAa > 0, \ \forall a \neq \left(\begin{array}{cccc} 0 \\ 0 \\ 0 \\ . \\ . \\ . \\ 0 \end{array}\right)_{n*1}
如果:
a^TAa \geq 0, \ \forall a. A_{n*n} is said to be POSITIVE SEMI DEFINITE, in some books, this is also written as NON NEGATIVE DEFINITE.
在线性代数中,很容易找到positive-definite matrix的定义,那么我们为什么需要一个这样的矩阵呢?从上面那个“距离”的角度来说,我们需要这样的矩阵是因为我们要确保距离是大于等于0的,如果x和y是完全一样的,我们希望其距离为0,否则我们希望一个大于0的数来表示不同程度,因此我们把距离公式写成a^TAa的矩阵形式。
Variance-Covariance matrix 可以被证明是NON-NEGATIVE DEFINITE的,实际上通常是POSITIVE-DEFINITE的,在正态分布(高斯密度函数)下,我们认为Variance-Covariance matrix 是POSITIVE-DEFINITE的,这就是我们为什么会在高斯密度函数的分母上把它写成|\Sigma|^{1/2}的原因。如果Variance-Covariance matrix是non-negative definite的,就会有一些properties,比如矩阵的行列式是它的特征值(the determinant of matrix is product of its eigenvalues),所有的特征值都是大于等于0的,如果variance-covariance matrix是positive-definite的,那么所有eigenvalues都是严格大于0的,所以可以把它做分母。
Determinant
在线性代数里,Determinant是一个可以从方形矩阵中计算出来的值。矩阵的Determinant记做det(A)\ or \ detA \ or \ |A|。在几何学里,它被视作描述矩阵线性变换的scaling factor。
2x2的矩阵行列式计算方法为:
|A|=\left|\begin{array}{cccc} a & b \\ c & d \\ \end{array}\right|=ad - bc
更高阶的计算方法到参考文献的链接查看吧,mathjax不好写了。
Matrix inverse
在线性代数中,如果一个nxn的方阵A存在一个nxn的方阵B使其满足
AB=BA=I_n
则称A为可逆矩阵,B是A的逆。I_n是nxn的Identity Matrix,也被含糊地称为Unit Matrix,单位矩阵,对角线是1,其余是0。
Transpose of Matrix
在线性代数里,矩阵的转置就是行列元素的索引对调,记做A^T:
[A^T]_{ij}=[A]_{ji}
参考文献
- 印度的讲的贼好的MOOC
- 矩阵行列式(Determinant)
- 矩阵的逆(Inverse)
- 矩阵的转置