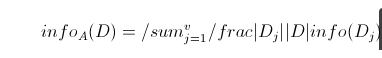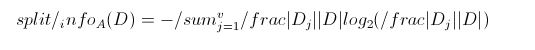这一篇文章中,讨论一种被广泛使用的分类算法——决策树(decision tree)。决策树的优势在于构造过程不需要任何领域知识或参数设置,因此在实际应用中,对于探测式的知识发现,决策树更加适用。
决策树案例
通俗来说,决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友,于是有了下面的对话:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别:见和不见。假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员,那么这个可以用下图表示女孩的决策逻辑。
上图完整表达了这个女孩决定是否见一个约会对象的策略,其中绿色节点表示判断条件,橙色节点表示决策结果,箭头表示在一个判断条件在不同情况下的决策路径,图中红色箭头表示了上面例子中女孩的决策过程。
这幅图基本可以算是一颗决策树,说它“基本可以算”是因为图中的判定条件没有量化,如收入高中低等等,还不能算是严格意义上的决策树,如果将所有条件量化,则就变成真正的决策树了。
有了上面直观的认识,我们可以正式定义决策树了:
决策树(decision tree)是一个树结构(可以是二叉树或非二叉树)。其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
可以看到,决策树的决策过程非常直观,容易被人理解。目前决策树已经成功运用于医学、制造产业、天文学、分支生物学以及商业等诸多领域。知道了决策树的定义以及其应用方法,下面介绍决策树的构造算法。
决策树的构造
不同于贝叶斯算法,决策树的构造过程不依赖领域知识,它使用属性选择度量来选择将元组最好地划分成不同的类的属性。所谓决策树的构造就是进行属性选择度量确定各个特征属性之间的拓扑结构。
构造决策树的关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支,其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。分裂属性分为三种不同的情况:
1、属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。
2、属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试,按照“属于此子集”和“不属于此子集”分成两个分支。
3、属性是连续值。此时确定一个值作为分裂点split_point,按照>split_point和<=split_point生成两个分支。
构造决策树的关键性内容是进行属性选择度量,属性选择度量是一种选择分裂准则,是将给定的类标记的训练集合的数据划分D“最好”地分成个体类的启发式方法,它决定了拓扑结构及分裂点split_point的选择。
属性选择度量算法有很多,一般使用自顶向下递归分治法,并采用不回溯的贪心策略。这里介绍ID3和c4.5两种常用算法。
ID3算法
从信息论知识中我们直到,期望信息越小,信息增益越大,从而纯度越高。所以ID3算法的核心思想就是以信息增益度量属性选择,选择分裂后信息增益最大的属性进行分裂。下面先定义几个要用到的概念。
设D为用类别对训练元组进行的划分,则D的熵表示为:
其中pi表示第i个类别在整个训练元组中出现的概率,可以用属于此类别元素的数量除以训练元组元素总数量作为估计。熵的实际意义表示是D中元组的类标号所需要的平均信息量。
现在我们假设将训练元组D按属性A进行划分,则A对D划分的期望信息为:
而信息增益即为两者的差值:
ID3算法就是在每次需要分裂时,计算每个属性的增益率,然后选择增益率最大的属性进行分裂。下面我们继续用SNS社区中不真实账号检测的例子说明如何使用ID3算法构造决策树。为了简单起见,我们假设训练集合包含10个元素:
其中s、m和l分别表示小、中和大。
设L、F、H和R表示日志密度、好友密度、是否使用真实头像和账号是否真实,下面计算各属性的信息增益。
因此日志密度的信息增益是0.276。
用同样方法得到H和F的信息增益分别为0.033和0.553。
因为F具有最大的信息增益,所以第一次分裂选择F为分裂属性,分裂后的结果如下图表示:
在上图的基础上,再递归使用这个方法计算子节点的分裂属性,最终就可以得到整个决策树。
上面为了简便,将特征属性离散化了,其实日志密度和好友密度都是连续的属性。对于特征属性为连续值,可以如此使用ID3算法:先将D中元素按照特征属性排序,则每两个相邻元素的中间点可以看做潜在分裂点,从第一个潜在分裂点开始,分裂D并计算两个集合的期望信息,具有最小期望信息的点称为这个属性的最佳分裂点,其信息期望作为此属性的信息期望。
C4.5算法
ID3算法存在一个问题,就是偏向于多值属性,例如,如果存在唯一标识属性ID,则ID3会选择它作为分裂属性,这样虽然使得划分充分纯净,但这种划分对分类几乎毫无用处。ID3的后继算法C4.5使用增益率的信息增益扩充,试图克服这个偏倚。
C4.5算法首先定义了“分裂信息”,其定义可以表示成:
其中各符号意义与ID3算法相同,然后,增益率被定义为:
C4.5选择具有最大增益率的属性作为分裂属性,其具体应用与ID3类似,不再赘述。
如果属性用完了怎么办
在决策树构造过程中可能会出现这种情况:所有属性都作为分裂属性用光了,但有的子集还不是纯净集,即集合内的元素不属于同一类别。在这种情况下,由于没有更多信息可以使用了,一般对这些子集进行“多数表决”,即使用此子集中出现次数最多的类别作为此节点类别,然后将此节点作为叶子节点。
关于剪枝
在实际构造决策树时,通常要进行剪枝,这时为了处理由于数据中的噪声和离群点导致的过分拟合问题。剪枝有两种:
先剪枝——在构造过程中,当某个节点满足剪枝条件,则直接停止此分支的构造。
后剪枝——先构造完成完整的决策树,再通过某些条件遍历树进行剪枝。
上图流程图就是一个假想的邮件分类系统决策树,正方形代表判断模块,椭圆形代表终止模块,表示已经得出结论,可以终止运行。判断模块引出的左右箭头称为分支,它可以到达另一个判断模块或者终止模块。决策树的主要优势在于数据形式非常容易理解。
优点
计算复杂度不高,对中间值的缺失不敏感,可以处理不相干特征数据,输出结果易于理解。
缺点
可能会产生过度匹配问题。
适用数据类型
数值型跟标称型
ID3算法python2实现
from math import log
import operator
#def createDataSet():自己创建的数据,可作实验用
#dataSet = [[1, 1, 'yes'],
# [1, 1, 'yes'],
# [1, 0, 'no'],
# [0, 1, 'no'],
# [0, 1, 'no']]
# labels = ['no surfacing','flippers']
#print dataSet
#change to discrete values
#return dataSet, labels
def loadDataSet(fileName): #general function to parse tab -delimited floats
dataMat = [] #assume last column is target value
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split(',')
fltLine = list(curLine) #map all elements to float()
dataMat.append(fltLine)
return dataMat
#def createDataSet():
#dataSet = [[1, 1, 'yes'],
#[1, 1, 'yes'],
#[1, 0, 'no'],
#[0, 1, 'no'],
#[0, 1, 'no']]
#labels = ['no surfacing','flippers']
#print dataSet
#change to discrete values
#return dataSet, labels
def calcShannonEnt(dataSet):#计算给定数据集的香农熵
numEntries = len(dataSet)#计算数据集中实例的总数
#print numEntries
labelCounts = {}#创建一个数据字典
for featVec in dataSet: #the the number of unique elements and their occurance
currentLabel = featVec[-1]#键值是最后一列数值
#print currentLabel
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0#如果键值不存在,则扩展字典并将当前键值加入字典
labelCounts[currentLabel] += 1#当前键值加入字典
#print labelCounts
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries# 使用所有类标签的发生概率计算类别出现的概率
#print prob
shannonEnt -= prob * log(prob,2) #log base 2 用这个概率计算香农熵
#print shannonEnt
return shannonEnt
def splitDataSet(dataSet, axis, value):#划分数据集,dataSet为待划分的数据集,axis为划分数据集的特征,value为特征的返回值
retDataSet = []#创建新的list对象
for featVec in dataSet:
#print featVec
if featVec[axis] == value:#将符合特征的数据抽取出来
reducedFeatVec = featVec[:axis] #chop out axis used for splitting
#print reducedFeatVec
reducedFeatVec.extend(featVec[axis+1:])#extend()函数只接受一个列表作为参数,并将该参数的每个元素都添加到原有的列表中
#print reducedFeatVec
retDataSet.append(reducedFeatVec)#append()向列表的尾部添加一个元素,任意,可以是tuple
return retDataSet
def chooseBestFeatureToSplit(dataSet):#遍历整个数据集,循环计算香农熵和splitDataSet()函数,找到最好的划分方式
numFeatures = len(dataSet[0]) - 1 #the last column is used for the labels判断当前数据集包含多少特征属性
baseEntropy = calcShannonEnt(dataSet)#计算整个数据集的原始香农熵,保存最初的无序度量值,用于与划分完之后的数据集计算的熵值进行比较
bestInfoGain = 0.0; bestFeature = -1
for i in range(numFeatures): #iterate over all the features 遍历数据集中的所有特征
featList = [example[i] for example in dataSet]#create a list of all the examples of this feature使用列表推导创建新的列表
uniqueVals = set(featList) #get a set of unique values将数据集中所有可能存在的值写入featlist中,并从列表中创建集合
newEntropy = 0.0
for value in uniqueVals:#遍历当前特征值中的所有唯一属性值,
subDataSet = splitDataSet(dataSet, i, value)#对每个特征划分一次数据集
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet) #计算数据集的新熵值,并对所有唯一特征值得到的熵求和
infoGain = baseEntropy - newEntropy #calculate the info gain; ie reduction in entropy#信息增益
if (infoGain > bestInfoGain): #compare this to the best gain so far#比较所有特征中的信息增益
bestInfoGain = infoGain #if better than current best, set to best
bestFeature = i#返回最好特征划分的索引值
return bestFeature #returns an integer
def majorityCnt(classList):
classCount={}#创建键值为classList中唯一值的数据字典,字典对象存储了classList中每个类标签现的频率
for vote in classList:
if vote not in classCount.keys(): classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)#利用operator操作键值排序字典
return sortedClassCount[0][0]#返回出现次数最多的分类名称
def createTree(dataSet,labels):#创建树的函数代码
classList = [example[-1] for example in dataSet]#创建了名为classList的列表变量,包含所有类标签
if classList.count(classList[0]) == len(classList): #
return classList[0]#stop splitting when all of the classes are equal
if len(dataSet[0]) == 1: #stop splitting when there are no more features in dataSet
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}#存储了树的所有信息
del(labels[bestFeat])#当前数据集选取的最好特征存储在变量bestFeat中,
featValues = [example[bestFeat] for example in dataSet]#得到列表包含的所有属性值
uniqueVals = set(featValues)
for value in uniqueVals:#遍历当前选择特征包含的所有属性值
subLabels = labels[:] #copy all of labels, so trees don't mess up existing labels为了保证每次调用函数createtree()时不改变原始列表的内容,使用新变量subLabels代替原始列表
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)#递归调用函数cteatetree()得到的返回值插入到字典变量mytree中
return myTree
def classify(inputTree,featLabels,testVec):#递归函数,
firstStr = inputTree.keys()[0]
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr)#使用index查找当前列表中第一个匹配firstStr变量的元素
key = testVec[featIndex]
valueOfFeat = secondDict[key]
if isinstance(valueOfFeat, dict): #如果到达叶子节点
classLabel = classify(valueOfFeat, featLabels, testVec)#返回当前节点的分类标签
else: classLabel = valueOfFeat
return classLabel
def storeTree(inputTree,filename):#决策树分类器的存储
import pickle#pickle序列化对象可以在磁盘上保存对象,并在需要时读出来
fw = open(filename,'w')
pickle.dump(inputTree,fw)
fw.close()
def grabTree(filename):
import pickle
fr = open(filename)
return pickle.load(fr)
import matplotlib.pyplot as plt
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
def getNumLeafs(myTree):#遍历整颗树,累计叶子节点的个数,并返回数值
numLeafs = 0
firstStr = myTree.keys()[0]#第一个关键字是以第一次划分数据集的类别标签
secondDict = myTree[firstStr]#表示子节点的数值
for key in secondDict.keys():#遍历整颗树的所有子节点
if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes type()函数判断子节点是否为字典类型,如果子节点是字典类型
numLeafs += getNumLeafs(secondDict[key])#则该节点是一个判断节点,递归调用getNumLeafs()函数
else: numLeafs +=1
return numLeafs
def getTreeDepth(myTree):#遍历过程中遇到判断节点的个数
maxDepth = 0
firstStr = myTree.keys()[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
thisDepth = 1 + getTreeDepth(secondDict[key])
else: thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotNode(nodeTxt, centerPt, parentPt, nodeType):#执行实际的绘图功能
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )#全局绘图区
def plotMidText(cntrPt, parentPt, txtString):#计算子节点与父节点的中间位置,在父节点间填充文本信息
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on计算宽与高
numLeafs = getNumLeafs(myTree) #this determines the x width of this tree计算树的宽
depth = getTreeDepth(myTree)#计算树的高
firstStr = myTree.keys()[0] #the text label for this node should be this
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)#标记子节点属性值
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
plotTree(secondDict[key],cntrPt,str(key)) #recursion
else: #it's a leaf node print the leaf node
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
#if you do get a dictonary you know it's a tree, and the first element will be another dict
def createPlot(inTree):#第一个版本的函数
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #no ticks
createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))#全局变量plotTree.totalW存储树的宽度
plotTree.totalD = float(getTreeDepth(inTree))#全局变量plotTree.totalD存储树的深度
plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;#使用plotTree.totalW,plotTree.totalD计算树节点的摆放位置,这样可以将树绘制在水平方向和垂直方向的中心位置
plotTree(inTree, (0.5,1.0), '')
plt.show()
#def createPlot():
#fig = plt.figure(1, facecolor='white')
#fig.clf()
#createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
#plotNode('a decision node', (0.5, 0.1), (0.1, 0.5), decisionNode)
#plotNode('a leaf node', (0.8, 0.1), (0.3, 0.8), leafNode)
#plt.show()
def retrieveTree(i):#输出预先存储的树信息,避免每次测试都要从数据集中创建树的麻烦,该函数主要用于测试,返回预定义的树结构
listOfTrees =[{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
{'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
]
return listOfTrees[i]
if __name__ == "__main__":
myMat=loadDataSet('C:\Users\HZF\Desktop\credit.txt')
labels=['A1','A2','A3','A4','A5','A6','A7','A8','A9','A10','A11','A12','A13','A14','A15']
myTree=createTree(myMat,labels)
print myTree
#numLeafs=getNumLeafs(myTree)
maxDepth=getTreeDepth(myTree)
print maxDepth
createPlot(myTree)
#classLabel=classify(myTree,labels,[1,1])
#labels=['age','prescript','astigmatic','tearRate']
#storeTree(myTree,'C:/Users/HZF/Desktop/machinelearninginaction/Ch03/classifierStorage.txt')
#pickle.load(fr)=grabTree('C:/Users/HZF/Desktop/machinelearninginaction/Ch03/classifierStorage.txt')
#print pickle.load(fr)
#print numLeafs
#print maxDepth
#print classLabel
#myMat,labels=createDataSet()
#myMat[0][-1]='maybe'
#print myMat
#shannonEnt=calcShannonEnt(myMat)
#print shannonEnt
#retDataSet=splitDataSet(myMat, 0, 0)
#print retDataSet
#bestFeature=chooseBestFeatureToSplit(myMat)
#print bestFeature
#myTree=createTree(myMat,labels)
#classify(inputTree,featLabels,testVec)
#print myTree
上篇就写这么多了,中下篇会尽快更新哦!
参考文献
1、《机器学习实战》(书)
2、算法杂货铺——分类算法之决策树(博客)
3、其他网站资料(略)