再看 KMP

教程见：学堂在线 -> 30240184X 数据结构 -> 第十一章

串匹配问题

串：长度往往远大于字符集的规模，元素重复率高
串匹配：对基于同一字符表的文本串 T[n] 和模式串 P[m]，判定 T 中是否存在某一子串与 P 相同，若存在（匹配），则报告该子串在 T 中的起始位置。串的长度 n 和 m
本身通常都很大，但相对而言 n 更大，即满足 2 << m << n。

暴搜

我一直想到的都是这样的版本，思路简单粗暴。用 i 标记对其位置，然后逐个字符比对，匹配就结束，不匹配到最后返回 -1：

int match_2(char *P, char *T, int m, int n){
    int i, j;
    for(i = 0; i < n - m + 1; i ++){ //i是对齐点
        for(j = 0; j < m; j ++){ //j指向比对的第j个字符
            if(T[i + j] != P[j]) break;
        }
        if(j == m) return i;
    }
    return -1;
}

这个版本更适合后面 KMP 算法套用，不同之处在于，它用 i 指示主串 T 正在接受匹配的字符， j 指示模式串 P 正在匹配的字符，而对齐位置其实是 i - j。然后，对于每次匹配或者不匹配，详细列出了操作，：

int match_1(char *P, char *T, int m, int n){
    //P[0:m) <- j; T[0:n) <- i;
    int i = 0, j = 0;
    while(i < n && j < m){
        if(T[i] == P[j]){ //如果匹配，都后移
            i ++, j ++;
        }else{
            i -= j - 1; j = 0; //不匹配，j归零，i回到刚刚匹配的对齐点的后一个
        }
    }
    return i - j;
}

测试了一个例子，这两种写法每一步比对都是一样的，复杂度是相同的。从match_2版本来看，复杂度是 O(n*m)，可以找到反例，每一次匹配都在最后一个字符失配。

改进思路

kmp思路.png

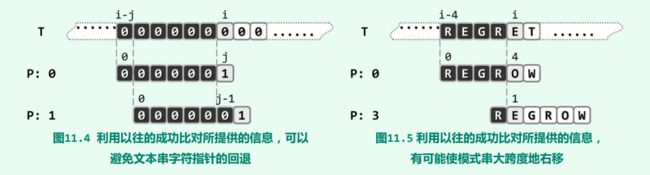
这两个例子可以看出改进的方向。对于左图，比对到 j 位置，一定是因为前面P[0,j)都比对成功，也就是“000000”。下一步比对难道还要从头开始，比对 6 个 0 才停下吗？一眼看上去，肯定知道前 5 个 0 都是比对成功的，从P[5]开始比对就可以了，j 只需要会退到 j - 1，而主串完全不必回退，i 仍然留在刚才失配的位置，等待下一次匹配。

对于右图，失配时，显然往后移动一步、两步都不会成功的，移动三步再开始就够了。

一般地，如果在图中位置 i 和 j 失配，可以将 T[i] 与P[t]对齐直接进行下一次匹配，这个 t 选做多少？

由前面匹配成功，T[i - j, i) = P[0, j)。

子串向右滑动后，如第三行，前缀能匹配，因此由图中1、2、3行匹配，T[i - t, i) = P[j - t, j) = P[0, t)。也就是说，P[0, j) 的长度为 t 的后缀，等于长度为 t 的前缀，即P[j - t, j) = P[0, t)。

这样的 t 可能不止一个，就像上面左图，5、4、3、2、1、0都能满足要求。但是为了不漏掉情况，选最大的 t ，也就是子串进行幅度最小的滑动。而且这个条件漂亮地脱离了与主串的关系，在这里能向后滑动多少，全部由子串本身就可以决定了。

next 表

既然与主串无关，可以依据子串先构造一个线性表 next。其中，next[j] 的具体含义是，对于P[0, j)，满足真前缀与真后缀相同的最大长度，也即P[j - t, j) = P[0, t)的最大的 t 。

这样，对于接下来计算的指导意义就是，当比对失配时，若主串位置为 i，子串位置为 j，则可以将子串的P[t]与主串T[i]做下一步比对，即子串向后滑动 j - t 个字符。

主算法

有了 next 表，只需要在前面的match_2中修改一下，失配的时候，i 不需要回退，j 滑到 next[j]，自然下一步就是P[t]与T[i]做比对了。

int match_kmp_1(char *P, char *T, int m, int n){
    //P[0:m) <- j; T[0:n) <- i;
    int next[m];
    buildNext(P, m, next);
    int i = 0, j = 0;
    while(i < n && j < m){
        printf("i = %d, j = %d\n", i, j);
        if(j < 0 || T[i] == P[j]){ //如果匹配，都后移。j=-1是假想的哨兵匹配
            i ++, j ++;
        }else{
            j = next[j]; //不匹配，i不动，只把j滑到next[j]
        }
    }
    return i - j;
}

这里还有一点，匹配的条件还有 j < 0。我倾向于理解这是个特殊约定：next[0]置为 -1 是比较合适的，因为数组P[0, j)没有长度，已经没有真前缀了，如果置为 0，那主算法将陷入死循环。这样一来，如果遇到T[i]与P[0]失配，按常理应该把 i 向后移动了，取 j = next[j]干嘛？为了写到一起去，索性仍然取j = next[j]，然后下一次循环里让它做i ++, j ++就正好达到效果。

教程的意思是，假想一个哨兵在P[-1]位置，它与任何字符都匹配。这样到了-1 的位置一定会匹配成功，自然i ++, j ++，也可以达到效果。总之， j < 0 是要当做匹配而处理的，写进匹配的条件。

next 的构造

void buildNext(char *P, int m, int* N){
    N[0] = -1;
    int j = 0, t = -1;
    while(j < m - 1){
        if(t < 0 || P[j] == P[t]){
            j ++, t ++;
            N[j] = t;     
        }else{
            t = N[t];
        }
    }
}

这里给出的 buildNext 我也是看了好久才看懂。这里的思路只是，假想将 P 字符串复制一份，然后自己与自己做匹配。同样，j 是指向所谓的“主串”，而 t 指向所谓“子串”。当匹配成功的时候，显然有更长的前缀等于后缀，而这个前后缀是对于P[0, j + 1)而言的，所以在都 ++ 之后再存到数组里正好，t 也就是那个前缀的长度。当匹配不成功，就和主算法一样，反正前面的 next 正好都算完了，只把 t 滑到 next[t]。

还有这个初始条件也想不出来，反正这样刚好启动……结束条件也是，因为j = m - 1 已经没有意义再算了，再算就算到 next[j] 了，不存在的。

线性时间

我真的乍一看是不明白为什么线性时间的。然而给一个辅助量 k = 2 * i - j，就会发现，主算法里面，每一轮循环，如果走上面分支，k ++；如果走下面分支，j 严格减小，k 增加。而 k 最大不过 2 * n，因此是线性的。同样，buildNext 其实也是一样的字符串匹配。所以整个算法是O(m+n)。

我严重怀疑以后遇上了我还得再学几次才能弄懂……