Python量化投资系列01 - SVR预测第二天开盘趋势和股价的正负统计分析

机器学习分类：

1. 监督学习：训练的输出分类是预先设定好的，根据输入和输出，算法的目标在于寻找其中的对应函数。
2. 无监督学习：训练的输出分类是预先不知道的。算法的目标在于发现数据中的结构，如聚类分析。
3. 半监督学习：介于监督学习和无监督学习之间。
4. 增强学习：算法通过执行一系列的动作，影响环境中的可观察变量，从而得到环境对动作反应的规律。最后根据这个规律，判断该采取何种行动以最大化某种回报。

监督式学习是机器学习的一个分支，可以通过训练样本而建立起一个输入和输出之间的函数，并以此对新的事件进行预测。

典型的监督学习流程

支持向量机

是监督学习中一种常用的学习方法。支持向量机（ Support Vector Machines SVM ）是一种比较好的实现了结构风险最小化思想的方法。它的机器学习策略是结构风险最小化原则 为了最小化期望风险，应同时最小化经验风险和置信范围）。

http://scikit-learn.org/stable/modules/svm.html#svm 中是SVM函数和简单介绍。

from sklearn.svm import SVR
# 可以构造支持向量回归（Support Vector Regression）模型

from sklearn.svm import SVC
# 可以用于分类（Support Vector Classification）

Support Vector Regression官网的一个简单例子：
http://scikit-learn.org/stable/auto_examples/svm/plot_svm_regression.html#example-svm-plot-svm-regression-py

import numpy as np
from sklearn.svm import SVR
import matplotlib.pyplot as plt
%matplotlib inline

# Generate sample data
X = np.sort(5 * np.random.rand(40, 1), axis=0)
y = np.sin(X).ravel()

# Add noise to targets
y[::5] += 3 * (0.5 - np.random.rand(8))
# Fit regression models
svr_rbf = SVR(kernel='rbf', C=1e3, gamma=0.2)
svr_lin = SVR(kernel='linear', C=1e3)
svr_poly = SVR(kernel='poly', C=1e3, degree=2)
y_rbf = svr_rbf.fit(X, y).predict(X)
y_lin = svr_lin.fit(X, y).predict(X)
y_poly = svr_poly.fit(X, y).predict(X)

# Result
lw = 2
plt.scatter(X, y, color='darkorange', label='data')
plt.hold('on')
plt.plot(X, y_rbf, color='navy', lw=lw, label='RBF model')
plt.plot(X, y_lin, color='c', lw=lw, label='Linear model')
plt.plot(X, y_poly, color='cornflowerblue', lw=lw, label='Polynomial model')
plt.xlabel('data')
plt.ylabel('target')
plt.title('Support Vector Regression')
plt.legend()
plt.show()

image.png

从回归的角度，可以根据之前的历史数据，预测下一个时间点的股价。
分类的角度，可以根据历史数据，预测下一个时间点股价的正负。
下面对股票数据进行回归建模。

import numpy as np
from sklearn.svm import SVR
import matplotlib.pyplot as plt
import time
import pandas as pd
%matplotlib inline

# Prep data
df = pd.read_csv("SHCOMP_CLOSE.csv")
df = df.set_index('TRADE_DATE').copy()
dates = df.index
X = np.mat(range(1, len(df.values)  + 1)).T
y = df.values

# Fit regression models
svr_rbf = SVR(kernel='rbf', C=1e3, gamma=0.1)
y_rbf = svr_rbf.fit(X, y).predict(X)
y_rbf

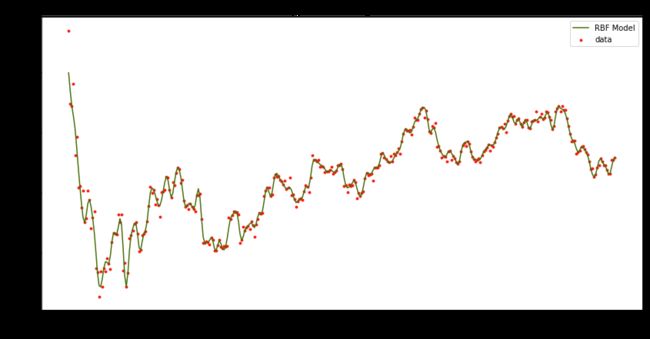
# Result
_, ax = plt.subplots(figsize=[14, 7])
ax.scatter(np.array(X), np.array(y), c='#F61909', label='data', s=8)
ax.plot(X, y_rbf, c='#486D0B', label='RBF Model')
# ax.plot(X, y, c='#000000', label='CLOSE')
ticks = ax.get_xticks()
plt.xlabel('data')
plt.ylabel('target')
plt.title('Support Vector Regression')
plt.legend()
plt.show()

上证综指预测结果

利用非监督学习甚至深度学习找到特征

比如找到大涨的股票，然后看大涨前一段时间的形态有没有相似的，利用非监督学习的方法。显然，这样的关系可能不是那么明显地存在于股票的价格中，可能存在于收益曲线中或者方差曲线中，甚至更高复杂度的统计量中。深度学习提供了将原数据投影到另一个特征空间中的方法，而且是高度非线性的。那么，原数据中没有体现出来的相关性，会不会在这种高度非线性的投影空间中体现出来呢？这个问题值思考。

举例：
特征选择：
基本面因子：PE，PB，ROE等
技术指标因子：RSI，KDJ，MA，MACD
蜡烛图形态因子：三乌鸦，锤子线等
输出
股价、股价涨跌分类、未来一段时间收益率

SVR (Support Vector Regression)

SVR是SVM(Support Vector Machine)中的一个版本，可以用于解决回归问题。
原理性参考这篇文章：A Tutorial on Support Vector Regression
简易中文版：Support Vector Regression

拟合与预测
假设i为1，days为30，
X：第i~i+days 天的开盘，收盘，最高，最低数据。
y：第i+1~i+days+1 天（对应的第二天）的开盘价。
X2：第i~i+days+1天的开盘，收盘，最高，最低数据。
yrep：第i+1~i+days+2天（对应的第二天）的预测开盘价。
yreal：第i+1~i+days+2天的开盘价。
yreal2：第i+days+2天的开盘价减第i+days+1天的开盘价。（真实趋势，大于0表示涨了）
yrep2：第i+days+2天的开盘价减第i+days+1天的预测开盘价。（预测趋势，大于0表示涨了）

同号相乘大于零，这里统计的是所有预测趋势的正确数量，预测涨和跌都算在里面了。

t：预测成功次数。

后面的两个if统计的是当预测为涨的时候，实际涨的次数和跌的次数。这个胜率只统计预测涨的成功率。

m：预测上涨，且真实情况上涨的次数。
e：预测上涨，但真实情况下跌的次数。

---

代码

import numpy as np
from sklearn.svm import SVR
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import preprocessing
%matplotlib inline

# Prep data
df = pd.read_csv("SHCOMP_QUOTE.csv")
df = df.set_index('DATE').copy()
dates = df.index
data = np.array(df[['OPEN', 'CLOSE', 'HIGH', 'LOW']])
data = preprocessing.scale(data)

# Prediction
i = 30
t = 0.0
m = 0.0
e = 0.0
days = 30
predict_value = 0 # OPEN CLOSE HIGH LOW
for i in range(data.shape[0] - days - 1):
    X = data[i: i + days, :]
    y = data[i + 1: i + days + 1, predict_value]
    svr = SVR(kernel='rbf', C=1e3, gamma=0.1)
    svr.fit(X, y)
    
    X2 = data[i: i + days + 1, :]
    y_pre = svr.predict(X)
    y_real = data[i + 1: i + days + 2, predict_value]
    
    y_real2 = y_real[-1] - y_real[-2]
    y_pre2 = y_pre[-1] - y_pre[-2]
    
    if y_real2 * y_pre2 > 0:
        t = t + 1
        
    if y_pre2 > 0:
        if y_real2 > 0:
            m = m + 1
        else:
            e = e + 1
            
print(t / (480 - days) * 100)
print(m / (m + e) * 100)

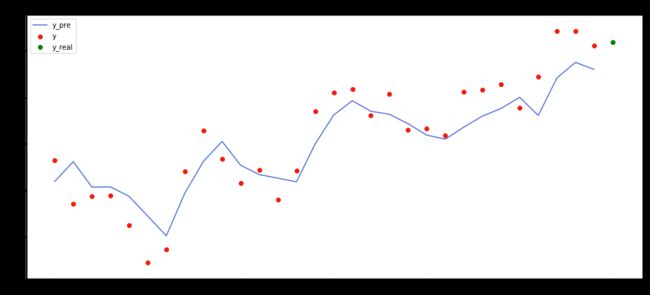
# Result
_, ax = plt.subplots(figsize=[16, 7])
plt.scatter(range(days), y, c='#F61909', label='y')
plt.hold('on')

plt.scatter(range(days, days + 1), y_real[-1], c='g', label='y_real')
plt.hold('on')

plt.plot(range(days), y_pre, c='#486DDB', label='y_pre')
plt.xlabel = ('day')
plt.ylabel = ('price')
plt.title('Support Vector Regression')
plt.legend()
plt.show()

image.png

图中蓝线代表的是预测的走势，红点代表输入的训练集，绿点代表未来值。

---