行列构成的矩阵(稀疏矩阵)
即是矩阵由3列构成,矩阵的行号,矩阵的列号,矩阵的值,值为0的部分省略。
比如:下面矩阵是行列构成的稀疏矩阵
Row为矩阵的行,Column为矩阵的列,Ainverse为矩阵的在某行某列的值。
Row Column Ainverse
1 1 1 1.83
2 2 1 0.50
3 2 2 2.03
4 3 1 -1.00
5 3 2 -1.00
6 3 3 2.50
7 4 1 -0.67
8 4 3 0.50
9 4 4 1.83
10 5 2 0.53
11 5 3 -1.00
12 5 4 -1.00
13 5 5 2.53
14 6 2 -1.07
15 6 5 -1.07
16 6 6 2.13
矩阵形式(半三角)
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1.83 0.00 0.0 0.00 0.00 0.00
[2,] 0.50 2.03 0.0 0.00 0.00 0.00
[3,] -1.00 -1.00 2.5 0.00 0.00 0.00
[4,] -0.67 0.00 0.5 1.83 0.00 0.00
[5,] 0.00 0.53 -1.0 -1.00 2.53 0.00
[6,] 0.00 -1.07 0.0 0.00 -1.07 2.13
矩阵形式(全三角)
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1.83 0.50 -1.0 -0.67 0.00 0.00
[2,] 0.50 2.03 -1.0 0.00 0.53 -1.07
[3,] -1.00 -1.00 2.5 0.50 -1.00 0.00
[4,] -0.67 0.00 0.5 1.83 -1.00 0.00
[5,] 0.00 0.53 -1.0 -1.00 2.53 -1.07
[6,] 0.00 -1.07 0.0 0.00 -1.07 2.13
R语言代码
id <- c(3,4,5,6)
sire <- c(1,1,4,5)
dam <- c(2,"NA",3,2)
ped <- data.frame(id,sire,dam)
ped
library(asreml)
ainv <- asreml.Ainverse(ped)$ginv
ainv
# method 1
matinv <- sparseMatrix(i = ainv$Row,j = ainv$Column,x = ainv$Ainverse)
round(matinv,2)
matinv[upper.tri(matinv)] <- t(mat)[upper.tri(t(mat))]
round(matinv,2)
# method 2
ani <- ainv
n<-max(ani$Row,ani$Column)
mat=matrix(0,n,n)
mat[cbind(ani$Row,ani$Column)]<-ani$Ainverse
round(mat,2)
mat[upper.tri(mat)]=t(mat)[upper.tri(t(mat))]
round(mat,2)
# method 3
library(asreml)
mat3 <- asreml.sparse2mat(ainv)
round(mat3,2)
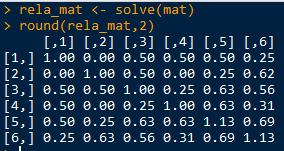
亲缘关系矩阵
如果对亲缘关系逆矩阵求逆,就得到亲缘关系矩阵了
代码如下
rela_mat <- solve(mat)
round(rela_mat,2)