一篇文章让你了解动态数组的数据结构的实现过程（Java 实现）

数组基础简单回顾

1. 数组是一种数据结构，用来存储同一类型值的集合。
2. 数组就是存储数据长度固定的容器，保证多个数据的数据类型要一致。
3. 数组是一种引用数据类型。
4. 简单来说，数组就是把需要存储的数据排成一排进行存放。
5. 数组的索引从 0 开始计数，最后一个位置的索引是数组的长度 - 1（n - 1）。
6. 可以使用数组的索引来存取数据。
7. 数组的索引可以有语意，也可以没有语意。
   • 例如，一个存储学生成绩的数组如果索引有语意，那么索引可以看成学生的学号，此时对于使用索引操作数组就可以看成对学号是 xxx 的学生进行存取成绩的操作。那么如果没有语意，就是随意存取学生的成绩到该数组中。
8. 数组最大的优点：快速查询。例如：arr[index]。
   • 根据此优点，可以知道数组最好应用于 “索引有语意” 的情况。因为索引有了语意，那么我们就可以知道要取的数据是什么、是在哪个位置，可以很方便地查询到数据。
   • 但也并非是所有有语意的索引都适用于数组，例如身份证号。我们知道，一个身份证号的号码有 18 位的长度，如果索引为一个身份证号，其对应着一个人，那么数组就要开启很大的空间，要开启空间到一个索引能有 18 位长度的数字这么大。那么此时如果只存取几个人，空间就会很浪费，而且这么多空间里并不是每一个索引都能是一个身份证号，有些是和身份证号的格式对应不上的，这些空间就会被浪费，所以并非是所有有语意的索引都适用于数组，要根据情况来决定使用。
9. 数组也可以处理“索引没有语意”的情况。比如一个数组有 10 个空间，其中前 4 个空间有数据，此时索引没有语意，对于用户而言，后面的空间是没有元素的，那么此时如何处理我们需要进行考虑。所以我们可以根据 Java 的数组来二次封装一个数组类来进行处理“索引没有语意”的情况，以此掌握数组这个数据结构。

---

二次封装数组类设计

基本设计

• 这里我将这个封装的数组类取名为 Array，其中封装了一个 Java 的静态数组 data[] 变量，然后基于这个 data[] 进行二次封装实现增、删、改、查的操作。接下来将一一实现。

• 成员变量设计

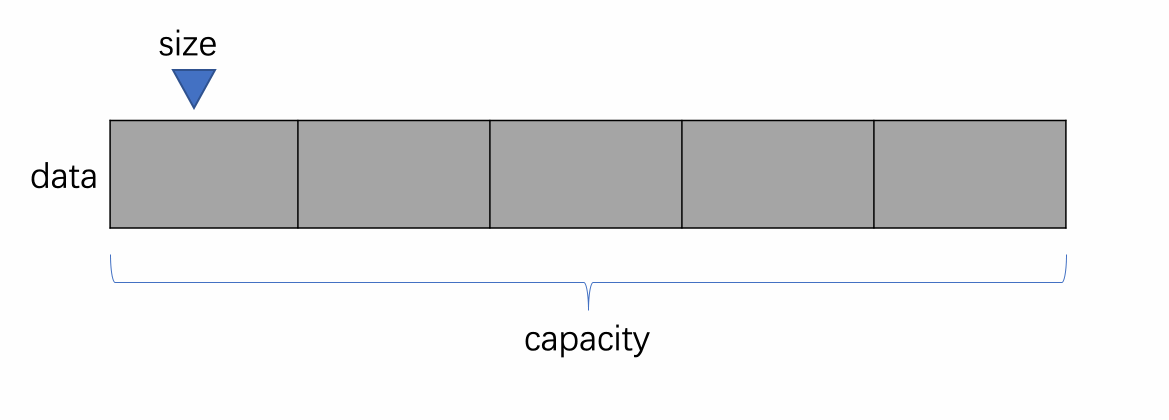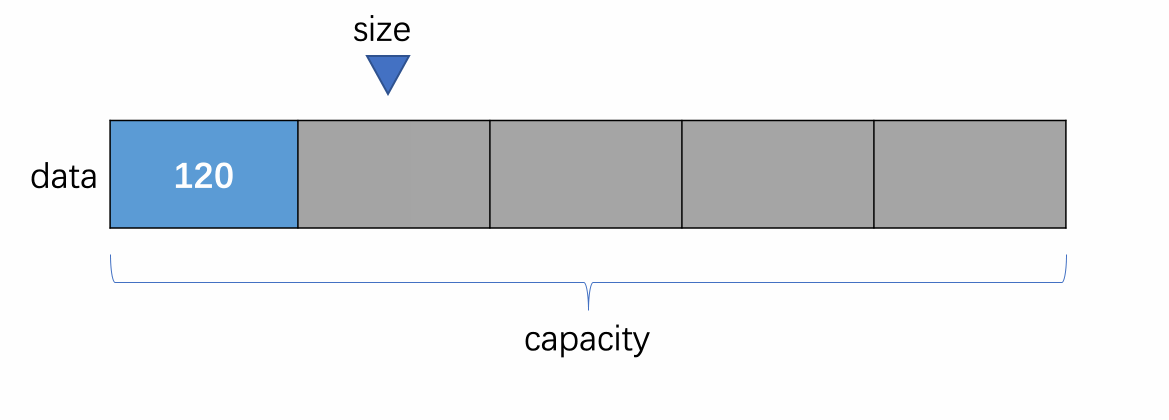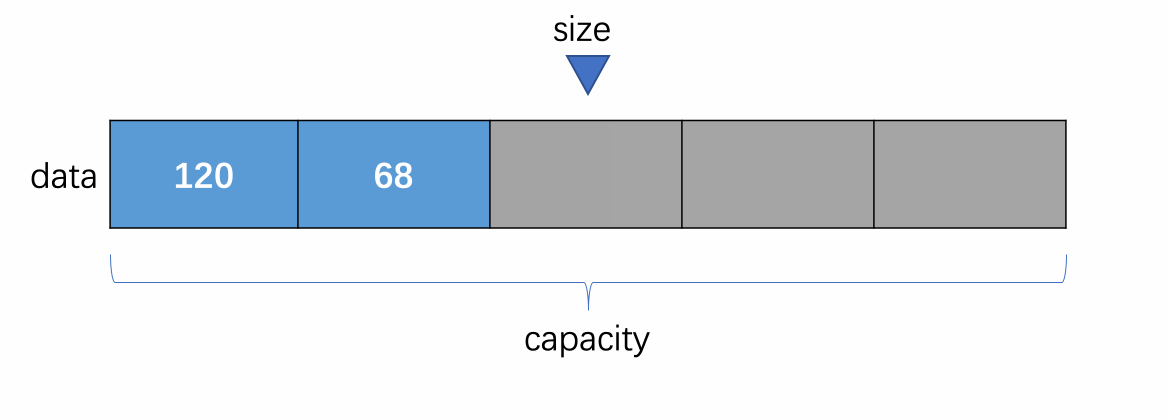
  • 由于数组本身是静态的，在创建的时候需指定大小，此时我将这个大小用变量 capacity 表示，即容量，表示数组空间最多装几个元素。但并不需要在类中声明，只需在构造函数的参数列表中声明即可，因为数组的容量也就是 data[] 的长度，不需要再声明一个变量来进行维护。

  • 对于数组中实际拥有的元素个数，这里我用变量 size 来表示。初始时其值为 0。

    • 这个 size 也能表示为数组中第一个没有存放元素的位置。
    • 例如数组为空时，size 为 0，此时索引 0 处为数组中第一个没有存放元素的位置；再如数组中有两个元素时，size 为 2，此时索引 0 和 1 处都有元素，索引 2 处没有，也就是数组中第一个没有存放元素的位置。

  • 所以可先创建 Array 类如下所示：

    /**
     * 基于静态数组封装的数组类
     *
     * @author 踏雪彡寻梅
     * @date 2019-12-17 - 22:26
     */
    public class Array {
    
        /**
         * 静态数组 data,基于该数组进行封装该数组类
         * data 的长度对应其容量
         */
        private int[] data;
    
        /**
         * 数组当前拥有的元素个数
         */
        private int size;
    
        /**
         * 默认构造函数,用户不知道要创建多少容量的数组时使用
         * 默认创建容量为 10 的数组
         */
        public Array() {
            // 默认创建容量为 10 的数组
            this(10);
        }
    
        /**
         * 构造函数,传入数组的容量 capacity 构造 Array
         * @param capacity 需要开辟的数组容量,由用户指定
         */
        public Array(int capacity) {
            // 初始化 data[] 和 size
            data = new int[capacity];
            size = 0;
        }
    
        /**
         * 获得数组当前的元素个数
         * @return 返回数组当前的元素个数
         */
        public int getSize() {
            return size;
        }
    
        /**
         * 获得数组的容量
         * @return 返回数组的容量
         */
        public int getCapacity() {
            // data[] 的长度对于其容量
            return data.length;
        }
    
        /**
         * 判断数组是否为空
         * @return 数组为空返回 true;否则返回 false
         */
        public boolean isEmpty() {
            // 当前 data[] 的元素个数为 0 代表数组为空,否则非空
            return size == 0;
        }
    
    }
    

---

向数组中添加元素

• 对于向数组中添加元素，向数组末尾添加元素是最简单的，原理如下：

  • 显而易见，往数组末尾添加元素是添加操作中最简单的操作，因为我们已经知道 size 这个变量指向的是数组第一个没有元素的地方，很容易理解，size 这个位置就是数组末尾的位置，所以往这个位置添加元素时也就是往数组末尾添加元素了，添加后维护 size 的值将其加一即可。当前添加时也需要注意数组空间是否已经满了。

  • 添加过程如下图所示：
    

  • 用代码来表示就如下所示：

    /**
     * 向数组末尾添加一个新元素
     * @param element 添加的新元素
     */
    public void addLast(int element) {
        // 检查数组空间是否已满
        if (size == data.length) {
            // 抛出一个非法参数异常表示向数组末尾添加元素失败,因为数组已满
            throw new IllegalArgumentException("AddLast failed. Array is full.");
        }
        // 在数组末尾添加新元素
        data[size] = element;
        // 添加后维护 size 变量
        size++;
    }
    

• 当然，也不能总是往数组末尾添加元素，当用户有往指定索引位置添加元素的需求时，也要将其实现：

  • 对于往指定索引位置添加元素：首先需要做的便是将该索引位置及其后面所有的元素都往后面移一个位置，将这个索引位置空出来。

    • 需要注意：并不是真的空出来，这个位置如果之前有元素的话还是存在原来的元素，只不过已经为原来元素制作了一个副本并将其往后移动了一个位置。

  • 其次再将元素添加到该索引位置。

    • 如果这个位置之前有元素的话实质上就是将新元素覆盖到原来的元素上。

  • 最后再维护存储数组当前元素个数的变量 size 将其值加一。

  • 当然在插入的时候也要确认数组是否有足够的空间以及确认插入的索引位置是否合法（该位置的合法值应该为 0 到 size 这个范围）。

  • 具体过程如下图所示：
    

  • 用代码来表示该过程就如下所示：

    /**
     * 在数组的 index 索引处插入一个新元素 element
     * @param index 要插入元素的索引
     * @param element 要插入的新元素
     */
    public void add(int index, int element) {
        // 检查数组空间是否已满
        if (size == data.length) {
            // 抛出一个非法参数异常表示向数组指定索引位置添加元素失败,因为数组已满
            throw new IllegalArgumentException("Add failed. Array is full.");
        }
    
        // 检查 index 是否合法
        if (index < 0 || index > size) {
            // 抛出一个非法参数异常表示向数组指定索引位置添加元素失败,应该让 index 在 0 到 size 这个范围才行
            throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
        }
    
        // 将 index 及其后面所有的元素都往后面移一个位置
        for (int i = size - 1; i >= index; i--) {
            data[i + 1] = data[i];
        }
        // 将新元素 element 添加到 index 位置
        data[index] = element;
    	// 维护 size 变量
        size++;
    }
    

  • 在实现这个方法之后，对于之前实现的 addLast 方法又可以进行简化了，只需在其中复用 add 方法，将 size 变量和要添加的元素变量 element 传进去即可。如下所示：

    /**
     * 向数组末尾添加一个新元素
     * @param element 添加的新元素
     */
    public void addLast(int element) {
    	// 复用 add 方法实现该方法
        add(size, element);
    }
    

  • 同理，也可再依此实现一个方法实现往数组首部添加一个新元素，如下所示：

    /**
     * 在数组首部添加一个新元素
     * @param element 添加的新元素
     */
    public void addFirst(int element) {
    	// 复用 add 方法实现该方法
        add(0, element);
    }
    

• 对于添加操作的基本实现，已经编写完成，接下来就继续实现在数组中查询元素和修改元素这两个操作。

---

在数组中查询元素和修改元素

• 查询元素时我们需要直观地知道数组中的信息，所以在查询元素和修改元素之前需要先重写 toString 方法，以让后面我们可以直观地看到数组中的信息，实现如下：

  /**
   * 重写 toString 方法,显示数组信息
   * @return 返回数组中的信息
   */
  @Override
  public String toString() {
      StringBuilder arrayInfo = new StringBuilder();
      arrayInfo.append(String.format("Array: size = %d, capacity = %d\n", size, data.length));
      arrayInfo.append("[");
      for (int i = 0; i < size; i++) {
          arrayInfo.append(data[i]);
          // 判断是否为最后一个元素
          if (i != size - 1) {
              arrayInfo.append(", ");
          }
      }
      arrayInfo.append("]");
      return arrayInfo.toString();
  }
  

• 那么接下来就可以实现这些操作了，首先先实现查询的方法:

  • 这里实现一个获取指定索引位置的元素的方法提供给用户用于查询指定位置的元素：

    • 对于这个方法，我们知道这个类是基于一个静态数组 data[] 进行封装的，那么对于获取指定索引位置的元素，我们只需使用 data[index] 就可获取到相应的元素，并且对用户指定的索引位置 index 进行合法性检测即可。

    • 同时，对于 data 我们之前已经做了 private 处理，那么使用该方法来封装获取元素的操作也可以避免用户直接对 data 进行操作，并且在此方法中进行了 idnex 的合法性检测。那么对于用户而言，对于数组中未使用的空间，他们是永远访问不到的，这保证了数据的安全，他们只需知道数组中已使用的空间中的元素能够进行访问即可。

    • 具体代码实现如下：

      /**
       * 获取 index 索引位置的元素
       * @param index 要获取元素的索引位置
       * @return 返回用户指定的索引位置处的元素
       */
      public int get(int index) {
          // 检查 index 是否合法
          if (index < 0 || index >= size) {
              // 抛出一个非法参数异常表示获取 index 索引位置的元素失败,因为 index 是非法值
              throw new IllegalArgumentException("Get failed. Index is illegal.");
          }
      
          // 返回用户指定的索引位置处的元素
          return data[index];
      }
      

• 同理，可以实现修改元素的方法如下：

  /**
   * 修改 index 索引位置的元素为 element
   * @param index 用户指定的索引位置
   * @param element 要放到 index 处的元素
   */
  public void set(int index, int element) {
      // 检查 index 是否合法
      if (index < 0 || index >= size) {
          // 抛出一个非法参数异常表示修改 index 索引位置的元素为 element 失败,因为 index 是非法值
          throw new IllegalArgumentException("Set failed. Index is illegal.");
      }
  
      // 修改 index 索引位置的元素为 element
      data[index] = element;
  }
  

  • 该方法实现的内容则是修改指定位置的老元素为新元素，同样也进行了 index 的合法性检测，对于用户而言是修改不了数组的那些未使用的空间的。

• 实现了以上方法，就可以接着实现数组中的包含、搜索和删除这些方法了。

---

数组中的包含、搜索和删除元素

• 在很多时候，我们在数组中存储了许多元素，有时需要知道这些元素中是否包含了某个元素，这时候就要实现一个方法来判断数组中是否包含我们需要的元素了：

  • 对于该方法，实现起来也很容易，只需遍历整个数组，逐一判断是否包含有需要的元素即可，实现如下：

    /**
     * 查找数组中是否有元素 element
     * @param element 用户需要知道是否存在于数组中的元素
     * @return 如果数组中包含有 element 则返回 true;否则返回 false
     */
    public boolean contains(int element) {
        // 遍历数组,逐一判断
        for (int i = 0; i < size; i++) {
            if (data[i] == element) {
                return true;
            }
        }
    
        return false;
    }
    

• 不过有些时候用户不仅需要知道数组中是否包含需要的元素，还需要知道其所在的索引位置处，这时候就要实现一个方法来搜索用户想要知道的元素在数组中的位置了：

  • 对于这个方法，具体实现和上面的包含方法差不多，也是遍历整个数组然后逐一判断，不同的是如果存在需要的元素则是返回该元素的索引，如果不存在则返回 -1 表示没有找到，实现如下：

    /**
     * 查找数组中元素 element 所在的索引
     * @param element 进行搜索的元素
     * @return 如果元素 element 存在则返回其索引;不存在则返回 -1
     */
    public int find(int element) {
        // 遍历数组,逐一判断
        for (int i = 0; i < size; i++) {
            if (data[i] == element) {
                return i;
            }
        }
    
        return -1;
    }
    

• 最后，则实现在数组中删除元素的方法，先实现删除指定位置元素的方法：

  • 对于删除指定位置元素这个方法，其实和之前实现的在指定位置添加元素的方法的思路差不多，只不过反转了过来。

  • 对于删除来说，只需从指定位置后一个位置开始，把指定位置后面的所有元素一一往前移动一个位置覆盖前面的元素，最后再维护 size 将其值减一并且返回删除的元素，就完成了删除指定位置的元素这个操作了，当然也需要进行指定位置的合法性判断。

    • 此时完成了删除之后，虽然 size 处还可能含有删除之前的数组的最后一个元素或者含有数组的默认值。（创建数组时，每个位置都有一个默认值 0）。但对用户而言，这个数据他们是拿不到的。因为对于获取元素的方法，已经设置了 index 的合法性检测，其中限制了 index 的范围为大于等于 0 且小于 size，所以 size 这个位置的元素用户是取不到的。综上该位置如含有之前的元素是不影响接下来的操作的。

  • 具体过程图示如下：
    

  • 代码实现如下：

    /**
     * 从数组中删除 index 位置的元素并且返回删除的元素
     * @param index 要删除元素的索引
     * @return 返回删除的元素
     */
    public int remove(int index) {
        // 检查 index 是否合法
        if (index < 0 || index >= size) {
            // 抛出一个非法参数异常表示从数组中删除 index 位置的元素并且返回删除的元素失败,因为 index 是非法值
            throw new IllegalArgumentException("Remove failed. Index is illegal.");
        }
    
        // 存储待删除的元素,以便返回
        int removeElement = data[index];
    
        for (int i = index + 1; i < size; i++) {
            data[i - 1] = data[i];
        }
        // 维护 size
        size--;
    
        // 返回删除的元素
        return removeElement;
    }
    

  • 实现了删除指定位置的元素的方法之后，我们可以根据该方法再衍生出两个简单的方法：删除数组中第一个元素的方法、删除数组中最后一个元素的方法。实现如下：

    • 删除数组中第一个元素：

      /**
       * 从数组中删除第一个元素并且返回删除的元素
       * @return 返回删除的元素
       */
      public int removeFirst() {
          // 复用 remove 方法实现该方法
          return remove(0);
      }
      

    • 删除数组中最后一个元素：

      /**
       * 从数组中删除最后一个元素并且返回删除的元素
       * @return 返回删除的元素
       */
      public int removeLast() {
          // 复用 remove 方法实现该方法
          return remove(size - 1);
      }
      

  • 还可以根据 remove 方法结合上之前实现的 find 方法实现一个删除指定元素 element 的方法：

    • 该方法实现逻辑为：

      • 先通过 find 方法查找这个需要删除的元素 element，如果找的到则会返回该元素的索引，再使用该索引调用 remove 方法进行删除并且返回 true。
      • 如果找不到则返回 false。

    • 实现如下：

      /**
       * 从数组中删除元素 element
       * @param element 用户指定的要删除的元素
       * @return 如果删除 element 成功则返回 true;否则返回 false
       */
      public boolean removeElement(int element) {
          // 使用 find 方法查找该元素的索引
          int index = find(element);
          // 如果找到,进行删除
          if (index != -1) {
          remove(index);
              return true;
      } else {
              return false;
          }
      }
      

    • 需要注意的是当前数组中是可以存在重复的元素的，如果存在重复的元素，在进行以上操作后只是删除了一个元素，并没有完全删除掉数组中的所有这个元素。对于 find 方法也是如此，如果存在重复的元素，那么查找到的索引则是第一个查找到的元素的索引。

    • 所以可以接着再实现一个能删除数组中重复元素的方法 removeAllElement:

      • 对于该方法，实现逻辑为：

        • 先使用 find 方法寻找一次用户指定要删除元素 element 的索引 index。
        • 再使用 while 循环对 index 进行判断：
          • 如果 index 不等于 -1，则在循环中调用 remove 方法将第一次查找到的索引传进去进行删除。
          • 然后再次使用 find 方法查找是否还有该元素再在下一次循环中进行判断。
          • 以此类推直到循环结束就可以删除掉数组中所有的该元素了。

      • 为了判断数组中是否有进行过删除操作，我使用了一个变量 i 来记录删除操作的次数：

        • 如果 while 循环结束后 i 的值大于 0 则表示进行过删除操作，此时返回 true 代表删除元素成功，反之返回 false 代表没有这个元素进行删除。

      • 具体实现代码如下：

        /**
         * 删除数组中的所有这个元素 element
         * @param element 用户指定的要删除的元素
         * @return 删除成功返回 true;否则返回 false
         */
        public boolean removeAllElement(int element) {
            // 使用 find 方法查找该元素的索引
            int index = find(element);
            // 用于记录是否有删除过元素 element
            int i = 0;
        
            // 通过 white 循环删除数组中的所有这个元素
            while (index != -1) {
                remove(index);
                index = find(element);
            i++;
            }
        
            // 有删除过元素 element,返回 true
            // 找不到元素 element 进行删除,返回 false
            return i > 0;
        }
        

      • 对于查找一个元素在数组中的所有索引的方法这里就不再实现了，有兴趣的朋友可以自行实现。

• 至此，这个类当中的基本方法都基本实现完成了，接下来要做的操作便是使用泛型对这个类进行一些改造使其更加通用，能够存放 “任意” 数据类型的数据。

---

使用泛型使该类更加通用（能够存放 “任意” 数据类型的数据）

• 我们知道对于泛型而言，是不能够存储基本数据类型的，但是这些基本数据类型都有相对应的包装类，所以对于这些基本数据类型只需使用它们对应的包装类即可。

• 对于将该类修改成泛型类非常简单，只需要更改几个地方即可，不过需要注意以下几点：

  1. 对于泛型而言，Java 是不支持形如 data = new E[capacity]; 直接 new 一个泛型数组的，需要绕一个弯子来实现，如下所示：

     data = (E[]) new Object[capacity];
     

  2. 在上面实现 contains 方法和 find 方法时，我们在其中进行了数据间的对比操作：if (data[i] == element)。在我们将类转变为泛型类之后，我们需要对这个判断做些修改，因为在使用泛型之后，我们数组中的数据是引用对象，我们知道引用对象之间的对比使用 equals 方法来进行比较为好，所以做出了如下修改：

     if (data[i].equals(element)) {
         ...
     }
     

  3. 如上所述，在使用了泛型之后，数组中的数据都是引用对象，所以在 remove 方法的实现中，对于维护 size 变量之后，我们已经知道此时 size 的位置是可能存在之前数据的引用的，所以此时我们可以将 size 这个位置置为 null，让垃圾回收可以较为快速地将这个不需要的引用回收，避免对象的游离。修改如下：

     /**
      * 从数组中删除 index 位置的元素并且返回删除的元素
      * @param index 要删除元素的索引
      * @return 返回删除的元素
      */
     public E remove(int index) {
         ...
         
         // 维护 size
         size--;
         // 释放 size 处的引用,避免对象游离
         data[size] = null;
     	
         ...
     }
     

• 将该类转变为泛型类的总修改如下所示：

  public class Array {
  
      /**
       * 静态数组 data,基于该数组进行封装该数组类
       * data 的长度对应其容量
       */
      private E[] data;
  
      /**
       * 数组当前拥有的元素个数
       */
      private int size;
  
      /**
       * 默认构造函数,用户不知道要创建多少容量的数组时使用
       */
      public Array() {
          // 默认创建容量为 10 的数组
          this(10);
      }
  
      /**
       * 构造函数,传入数组的容量 capacity 构造 Array
       * @param capacity 需要开辟的数组容量,由用户指定
       */
      public Array(int capacity) {
          // 初始化 data
          data = (E[]) new Object[capacity];
          size = 0;
      }
  
      /**
       * 获得数组当前的元素个数
       * @return 返回数组当前的元素个数
       */
      public int getSize() {
          return size;
      }
  
      /**
       * 获得数组的容量
       * @return 返回数组的容量
       */
      public int getCapacity() {
          return data.length;
      }
  
      /**
       * 判断数组是否为空
       * @return 数组为空返回 true;否则返回 false
       */
      public boolean isEmpty() {
          return size == 0;
      }
  
      /**
       * 在数组的 index 索引处插入一个新元素 element
       * @param index 要插入元素的索引
       * @param element 要插入的新元素
       */
      public void add(int index, E element) {
          // 检查数组空间是否已满
          if (size == data.length) {
              // 抛出一个非法参数异常表示向数组指定索引位置添加元素失败,因为数组已满
              throw new IllegalArgumentException("Add failed. Array is full.");
          }
  
          // 检查 index 是否合法
          if (index < 0 || index > size) {
              // 抛出一个非法参数异常表示向数组指定索引位置添加元素失败,应该让 index 在 0 到 size 这个范围才行
              throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
          }
  
          // 将 index 及其后面所有的元素都往后面移一个位置
          for (int i = size - 1; i >= index; i--) {
              data[i + 1] = data[i];
          }
          // 将新元素 element 添加到 index 位置
          data[index] = element;
          // 维护 size 变量
          size++;
      }
  
      /**
       * 在数组首部添加一个新元素
       * @param element 添加的新元素
       */
      public void addFirst(E element) {
          // 复用 add 方法实现该方法
          add(0, element);
      }
  
      /**
       * 向数组末尾添加一个新元素
       * @param element 添加的新元素
       */
      public void addLast(E element) {
          // 复用 add 方法实现该方法
          add(size, element);
      }
  
      /**
       * 获取 index 索引位置的元素
       * @param index 要获取元素的索引位置
       * @return 返回用户指定的索引位置处的元素
       */
      public E get(int index) {
          // 检查 index 是否合法
          if (index < 0 || index >= size) {
              // 抛出一个非法参数异常表示获取 index 索引位置的元素失败,因为 index 是非法值
              throw new IllegalArgumentException("Get failed. Index is illegal.");
          }
  
          // 返回用户指定的索引位置处的元素
          return data[index];
      }
  
      /**
       * 修改 index 索引位置的元素为 element
       * @param index 用户指定的索引位置
       * @param element 要放到 index 处的元素
       */
      public void set(int index, E element) {
          // 检查 index 是否合法
          if (index < 0 || index >= size) {
              // 抛出一个非法参数异常表示修改 index 索引位置的元素为 element 失败,因为 index 是非法值
              throw new IllegalArgumentException("Set failed. Index is illegal.");
          }
  
          // 修改 index 索引位置的元素为 element
          data[index] = element;
      }
  
      /**
       * 查找数组中是否有元素 element
       * @param element 用户需要知道是否存在于数组中的元素
       * @return 如果数组中包含有 element 则返回 true;否则返回 false
       */
      public boolean contains(E element) {
          // 遍历数组,逐一判断
          for (int i = 0; i < size; i++) {
              if (data[i].equals(element)) {
                  return true;
              }
          }
  
          return false;
      }
  
      /**
       * 查找数组中元素 element 所在的索引
       * @param element 进行搜索的元素
       * @return 如果元素 element 存在则返回其索引;不存在则返回 -1
       */
      public int find(E element) {
          // 遍历数组,逐一判断
          for (int i = 0; i < size; i++) {
              if (data[i].equals(element)) {
                  return i;
              }
          }
  
          return -1;
      }
  
      /**
       * 从数组中删除 index 位置的元素并且返回删除的元素
       * @param index 要删除元素的索引
       * @return 返回删除的元素
       */
      public E remove(int index) {
          // 检查 index 是否合法
          if (index < 0 || index >= size) {
              // 抛出一个非法参数异常表示从数组中删除 index 位置的元素并且返回删除的元素失败,因为 index 是非法值
              throw new IllegalArgumentException("Remove failed. Index is illegal.");
          }
  
          // 存储待删除的元素,以便返回
          E removeElement = data[index];
  
          for (int i = index + 1; i < size; i++) {
              data[i - 1] = data[i];
          }
          // 维护 size
          size--;
          // 释放 size 处的引用,避免对象游离
          data[size] = null;
  
          // 返回删除的元素
          return removeElement;
      }
  
      /**
       * 从数组中删除第一个元素并且返回删除的元素
       * @return 返回删除的元素
       */
      public E removeFirst() {
          // 复用 remove 方法实现该方法
          return remove(0);
      }
  
      /**
       * 从数组中删除最后一个元素并且返回删除的元素
       * @return 返回删除的元素
       */
      public E removeLast() {
          // 复用 remove 方法实现该方法
          return remove(size - 1);
      }
  
      /**
       * 从数组中删除元素 element
       * @param element 用户指定的要删除的元素
       * @return 如果删除 element 成功则返回 true;否则返回 false
       */
      public boolean removeElement(E element) {
          // 使用 find 方法查找该元素的索引
          int index = find(element);
          // 如果找到,进行删除
          if (index != -1) {
              remove(index);
              return true;
          } else {
              return false;
          }
      }
  
      /**
       * 删除数组中的所有这个元素 element
       * @param element 用户指定的要删除的元素
       * @return 删除成功返回 true;否则返回 false
       */
      public boolean removeAllElement(E element) {
          // 使用 find 方法查找该元素的索引
          int index = find(element);
          // 用于记录是否有删除过元素 element
          int i = 0;
  
          // 通过 white 循环删除数组中的所有这个元素
          while (index != -1) {
              remove(index);
              index = find(element);
              i++;
          }
  
          // 有删除过元素 element,返回 true
          // 找不到元素 element 进行删除,返回 false
          return i > 0;
      }
  
      /**
       * 重写 toString 方法,显示数组信息
       * @return 返回数组中的信息
       */
      @Override
      public String toString() {
          StringBuilder arrayInfo = new StringBuilder();
          arrayInfo.append(String.format("Array: size = %d, capacity = %d\n", size, data.length));
          arrayInfo.append("[");
          for (int i = 0; i < size; i++) {
              arrayInfo.append(data[i]);
              // 判断是否为最后一个元素
              if (i != size - 1) {
                  arrayInfo.append(", ");
              }
          }
          arrayInfo.append("]");
          return arrayInfo.toString();
      }
  }
  

• 此时可以做一些测试：

  • 测试代码：

    public static void main(String[] args) {
    	Array array = new Array<>(20);
        for (int i = 0; i < 10; i++) {
            array.addLast(i);
        }
        System.out.println(array + "\n");
    
        array.add(1, 20);
        System.out.println(array);
        array.addFirst(35);
        System.out.println(array);
        array.addLast(40);
        System.out.println(array + "\n");
    
        Integer e = array.remove(6);
        System.out.println("e: " + e);
        System.out.println(array + "\n");
        e = array.removeLast();
        System.out.println("e: " + e);
        System.out.println(array + "\n");
        e = array.removeFirst();
        System.out.println("e: " + e);
        System.out.println(array + "\n");
    
        int size = array.getSize();
        int capacity = array.getCapacity();
        System.out.println("size: " + size + ", capacity: " + capacity + "\n");
    
        e = array.get(3);
        System.out.println("e: " + e);
        array.set(3, 66);
        e = array.get(3);
        System.out.println("e: " + e);
        System.out.println(array + "\n");
    
        boolean empty = array.isEmpty();
        System.out.println("empty: " + empty);
    
        boolean contains = array.contains(9);
        System.out.println("contains: " + contains + "\n");
    
        int index = array.find(9);
        System.out.println(array);
        System.out.println("index: " + index + "\n");
    
        boolean b = array.removeElement(9);
        System.out.println(array);
        System.out.println("b: " + b + "\n");
    
        array.addLast(88);
        array.addLast(88);
        array.addLast(88);
        System.out.println(array);
        b = array.removeAllElement(88);
        System.out.println(array);
        System.out.println("b: " + b);
    }
    

  • 测试结果：

    Array: size = 10, capacity = 20
    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
    
    Array: size = 11, capacity = 20
    [0, 20, 1, 2, 3, 4, 5, 6, 7, 8, 9]
    Array: size = 12, capacity = 20
    [35, 0, 20, 1, 2, 3, 4, 5, 6, 7, 8, 9]
    Array: size = 13, capacity = 20
    [35, 0, 20, 1, 2, 3, 4, 5, 6, 7, 8, 9, 40]
    
    e: 4
    Array: size = 12, capacity = 20
    [35, 0, 20, 1, 2, 3, 5, 6, 7, 8, 9, 40]
    
    e: 40
    Array: size = 11, capacity = 20
    [35, 0, 20, 1, 2, 3, 5, 6, 7, 8, 9]
    
    e: 35
    Array: size = 10, capacity = 20
    [0, 20, 1, 2, 3, 5, 6, 7, 8, 9]
    
    size: 10, capacity: 20
    
    e: 2
    e: 66
    Array: size = 10, capacity = 20
    [0, 20, 1, 66, 3, 5, 6, 7, 8, 9]
    
    empty: false
    contains: true
    
    Array: size = 10, capacity = 20
    [0, 20, 1, 66, 3, 5, 6, 7, 8, 9]
    index: 9
    
    Array: size = 9, capacity = 20
    [0, 20, 1, 66, 3, 5, 6, 7, 8]
    b: true
    
    Array: size = 12, capacity = 20
    [0, 20, 1, 66, 3, 5, 6, 7, 8, 88, 88, 88]
    Array: size = 9, capacity = 20
    [0, 20, 1, 66, 3, 5, 6, 7, 8]
    b: true
    
    进程已结束，退出代码 0
    

• 在将这个类转换为泛型类以支持存储 “任意” 类型的数据之后，还可以对这个类进行一些修改，使其能够根据存储的数据量动态地扩展以及缩小自身的空间以节约资源。

---

升级为动态数组

• 对于动态数组，我们需要实现的效果为使其能够根据自身数据量的大小自动伸缩自身的空间，所以就相对应着两种情况：当数组空间满的时候进行扩容、当数组空间少到一定程度时进行减容。接下来一一实现。

• 当数组空间满的时候进行扩容

  • 对于这种情况，在我们先前的实现中，在数组空间用完时我们往其中添加新数据我们是不能再往数组中添加的，所以此时我们需要在 add 方法中做扩容操作以使能够添加新数据进去。

  • 对于扩容操作，可以实现一个更改容量的方法 resize来实现：

    1. 先构造一个容量为当前数组两倍的新数组 newData。

       • 对于为何扩容原来空间的两倍而不是扩容一个常数，是因为如果扩容一个常数不知道要扩容多少空间。
       • 比如原先已有几万个元素此时扩容几十个容量那是十分低效的，因为如果要再添加很多数据需要扩容很多次。
       • 又比如一次扩容很多容量又显得十分浪费，比如原有 10 个数据此时扩容 1000 个容量那么可能会有很多空间会被浪费。
       • 而对于扩容为原来容量的二倍（也可以扩容为其他倍数，如 1.5 倍），是和当前数组有多少容量是相关的，扩容的量和已有的容量是一个数量级的，比如原有容量为 100 那么扩容成 200，原有容量为 10000 那么扩容为 20000，这样子扩容是比较有优势的，之后会进行复杂度分析分析其中的优势。

    2. 使用循环将当前数组的数据一一复制到新数组中。

    3. 将当前数组的引用变量 data 引用到 newData 上。

    4. 对于 size 的操作依然还是之前 add 方法中的操作，不用在扩容方法中进行操作。

    5. 对于 data 之前的引用，因为此时 data 已经引用到了新数组上，没有其他变量引用它们，所以原来的引用会被垃圾回收自动回收掉。

    6. 对于 newData 这个变量由于它是局部变量在执行完添加数据这个方法之后会自动消失,不用对其进行额外的操作。

    7. 所以最后 data 这个变量引用的就是数组扩容后并添加了新数据后的所有数据。

  • 以上过程图示如下：
    

  • 修改过后的代码如下所示：

    /**
     * 在数组的 index 索引处插入一个新元素 element
     * @param index 要插入元素的索引
     * @param element 要插入的新元素
     */
    public void add(int index, E element) {
        // 检查 index 是否合法
        if (index < 0 || index > size) {
            // 抛出一个非法参数异常表示向数组指定索引位置添加元素失败,应该让 index 在 0 到 size 这个范围才行
            throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
        }
    
        // 检查数组空间是否已满,如果已满进行扩容,再进行添加数据的操作
        if (size == data.length) {
            // 对 data 进行扩容,扩容为原先容量的两倍
            resize(2 * data.length);
        }
    
        // 将 index 及其后面所有的元素都往后面移一个位置
        for (int i = size - 1; i >= index; i--) {
            data[i + 1] = data[i];
        }
        // 将新元素 element 添加到 index 位置
        data[index] = element;
        // 维护 size 变量
        size++;
    }
    
    /**
     * 更改 data 的容量
     * @param newCapacity data 的新容量
     */
    private void resize(int newCapacity) {
        E[] newData = (E[]) new Object[newCapacity];
        for (int i = 0; i < size; i++) {
            newData[i] = data[i];
        }
        data = newData;
    }
    

• 当数组空间少到一定程度时进行减容

  • 对于这种情况，在先前的 remove 方法实现中，删除了元素之后是没有进行别的操作的，此时我们需要进行一个判断，判断数组在删除元素后此时剩余的元素个数是否达到了一个比较小的值，如果达到我们就进行减容操作。此时先将这个值设定为数组原来容量的二分之一，如果剩余的元素个数等于这个值，这里先暂时将数组的容量减小一半。

  • 这时候就可以复用上面实现的更改数组容量的方法了，具体代码实现如下：

    /**
     * 从数组中删除 index 位置的元素并且返回删除的元素
     * @param index 要删除元素的索引
     * @return 返回删除的元素
     */
    public E remove(int index) {
        // 检查 index 是否合法
        if (index < 0 || index >= size) {
            // 抛出一个非法参数异常表示从数组中删除 index 位置的元素并且返回删除的元素失败,因为 index 是非法值
            throw new IllegalArgumentException("Remove failed. Index is illegal.");
        }
    
        // 存储待删除的元素,以便返回
        E removeElement = data[index];
    
        for (int i = index + 1; i < size; i++) {
            data[i - 1] = data[i];
        }
        // 维护 size
        size--;
        // 释放 size 处的引用,避免对象游离
        data[size] = null;
    
        // 判断当前 data 中的元素个数是否达到了该进行减容操作的个数,如果达到进行减容
        if (size == data.length / 2) {
            // 减容操作,减小容量为原先的二分之一
            resize(data.length / 2);
        }
    
        // 返回删除的元素
        return removeElement;
    }
    

• 至此，已经基本实现了动态数组该具有的功能，接着对当前实现的方法进行一些简单的时间复杂度分析以找到一些还能提升效率的地方进行修改使这个数组类更加完善。

---

简单的时间复杂度分析与一些改进

• 对于添加操作的时间复杂度分析

  • 对于添加操作，已经实现了三个方法，分别是：addLast、addFirst、add 方法。接下来一一简单地分析一下它们的时间复杂度：
    • addLast：对于这个方法，每一次添加都是在数组末尾直接赋值，不需要移动元素，所以可以得出该方法的时间复杂度为 O(1)。
    • addFirst：对于该方法，每一次添加都需要把数组所有元素往后移动一个位置以腾出第一个位置来放置新元素，可以得出该方法的时间复杂度为 O(n)。
    • add：对于该方法，可能有时在数组较前面添加、可能有时在数组较后面添加，但综合而言，移动元素的次数大约为 n/2，所以该方法的时间复杂度为 O(n/2) = O(n)。
    • 所以总的来说，添加操作的时间复杂度为 O(n)。（最坏情况）
    • 对于添加操作中的 resize 方法，每一次执行都会复制一次数组中的所有元素，所以该方法的时间复杂度为 O(n)。

• 对于删除操作的时间复杂度分析

  • 由上面的添加操作的时间复杂度分析可以很快的得出删除操作的时间复杂度如下：
    • removeLast：O(1)
    • removeFirst：O(n)
    • remove：O(n/2) = O(n)
    • 总的来说，删除操作的时间复杂度为 O(n)。（最坏情况）
    • 其中的 resize 方法上面已经分析过，时间复杂度为 O(n)。

• 对于修改操作的时间复杂度分析

  • 对于修改操作而言，实现了 set 方法，对于该方法存在两种情况：
    • 知道要修改元素的索引：如果知道索引，那么可以瞬间找出要修改的元素并修改为新元素，所以时间复杂度为 O(1)。
    • 不知道要修改元素的索引：如果不知道索引，可以借助 find 方法找到索引位置再进行修改，所以这种情况需要先找后改，时间复杂度为 O(n)。

• 对于查找操作的时间复杂度分析

  • 对于查询操作，实现了三个方法 get、contains、find：
    • get：该方法为使用索引获取元素，时间复杂度为 O(1)。
    • contains：该方法是一一判断元素是否存在，时间复杂度为 O(n)。
    • find：该方法是一一判断元素是否存在找到其位置，时间复杂度为 O(n)。
    • 总的来说，如果知道索引，查找操作时间复杂度为 O(1)；如果不知道索引，时间复杂度为 O(n)。

• 此时再着重观察一下添加和删除操作，如果我们总是只对最后一个元素进行操作（addLast 或 removeLast），那么此时时间复杂度是否还是为 O(n)?resize 方法是否会影响?

• 可以进行一些简单的分析：

• 首先先看 resize 方法，对于这个方法，是不是在每一次添加或删除元素时会影响到数组的性能呢？很显然不是的，对于 reszie 而言并不是每次执行添加和删除操作时都会触发它。

  • 比如一个数组初始容量为 10，那么它要执行 10 次添加操作才会执行一次 resize 方法，此时容量为 20，这时要再执行 10 次添加操作才会再执行 resize 方法，然后容量变为 40，这时需要执行 20 次添加操作才会再一次执行 resize 方法。

    • 即正常情况下，需要执行 n 次添加操作才会触发一次 resize 方法。

  • 接着进行如下分析：

    • 假设数组当前容量为 10，并且每一次添加操作都使用 addLast：
      • 前十次添加是没有任何问题的，进行了 10 次 addLast 操作。
      • 在第十一次添加时，触发了一次 resize 方法，此时复制 10 个元素，进行了 10 次基本操作。
      • 执行完 resize 方法之后，添加了第十一个元素，此时又进行了一次 addLast 操作。
      • 所以到此时，一共执行了 11 次 addLast 操作，触发了一次 resize，总共进行了 21 次基本操作。
      • 那么平均而言，每次 addLast 操作，大约进行 2 次基本操作。时间复杂度为 O(1)。
      • 以上可归纳如下：
        • 假设数组容量为 n，执行了 n+1 次 addLast，触发 resize，总共进行 2n+1 次基本操作，平均每次 addLast 操作进行大约 2 次基本操作，这样均摊计算，时间复杂度是 O(1) 的。

  • 同理，removeLast 操作的均摊复杂度也为 O(1)。

  • 不过此时，在我们之前的代码实现中还存在着一个特殊情况：同时进行 addLast 和 removeLast 操作（复杂度震荡）。

  • 以一个例子说明：

    • 假设当前数组容量已满为 n，此时进行一次 addLast 操作，那么会触发一次 resize 方法将容量扩容为 2n，然后紧接着又执行一次 removeLast 操作，此时元素个数为 n 为容量 2n 的一半又会触发一次 resize 方法，接着又执行一次 addLast 方法，再接着执行 removeLast 方法，以此类推，循环往复，resize 方法就会一直被触发，每次的时间复杂度都为 O(n)，这时再也不是如之前分析的那般每 n 次添加操作才会触发一次 resize 方法了，也就是不再均摊复杂度了，这种情况也就是复杂度震荡（从预想的 O(1) 一下上升到了 O(n)）。

    • 那么此时需要进行一些改进，从上面例子可以分析出出现这种特殊情况的原因：removeLast 时触发 resize 过于着急。

      • 也就是当元素个数为当前容量二分之一时就进行了减容操作，将容量减少为二分之一，此时容量是满的，这时再添加一个元素自然而然的就再一次触发 resize 方法进行扩容了。

    • 所以可以这样修改：在进行 removeLast 操作时，原先实现的判断元素个数等于容量的二分之一就进行减容的操作修改为当元素个数等于容量的四分之一时才进行减容操作，减少容量为原先的一半，这样子减容之后，还预留了一半的空间用于添加元素，避免了以上的复杂度震荡。

    • 所以修改代码如下（需要注意的是在减容的过程中可能数组容量会出现等于 1 的情况，如果容量为 1，传进 resize 方法的参数就是 1/2=0 了，这时会 new 一个空间为 0 的数组，所以需要避免这种情况）：

      /**
       * 从数组中删除 index 位置的元素并且返回删除的元素
       * @param index 要删除元素的索引
       * @return 返回删除的元素
       */
      public E remove(int index) {
          // 检查 index 是否合法
          if (index < 0 || index >= size) {
              // 抛出一个非法参数异常表示从数组中删除 index 位置的元素并且返回删除的元素失败,因为 index 是非法值
              throw new IllegalArgumentException("Remove failed. Index is illegal.");
          }
      
          // 存储待删除的元素,以便返回
          E removeElement = data[index];
      
          for (int i = index + 1; i < size; i++) {
              data[i - 1] = data[i];
          }
          // 维护 size
          size--;
          // 释放 size 处的引用,避免对象游离
          data[size] = null;
      
          // 当 size == capacity / 4 时,进行减容操作
          if (size == data.length / 4 && data.length / 2 != 0) {
              // 减容操作,减小容量为原先的二分之一
              resize(data.length / 2);
      }
      
          // 返回删除的元素
          return removeElement;
      }
      

• 至此，这个数组类就封装完成了，总的来说这个类基于一个静态数组实现了一个支持增删改查数据、动态更改数组空间和支持存储 “任意” 数据类型的数据的数组数据结构

---

如有写的不足的，请见谅，请大家多多指教。(*^▽^*)

---