如何激发孩子数学学习的内驱力?这8个国外宝藏网站满足你的所有期待!
看点 之前外滩君分享了美国停课后的312学习资源(点击查看)很多读者收藏并表示希望类似的资源推荐,因此在今天这篇文章中,外滩君就来推荐海外“数学学习资源”!根据操作便捷度、内容质量、页面设计等多个因素,选出了8个网站,并按照幼儿园、小学、初中、高中推荐给不同学龄段的孩子。因此,家长可以根据自身孩子的需求与能力挖掘更多、更适合的学习资料。
文丨陆以沁 编丨Jane
2019年年末,教育部发布的一份报告中显示,四年级学生数学学习焦虑程度高与较高的比例接近四分之一,而八年级学生,这个比例超过40%。
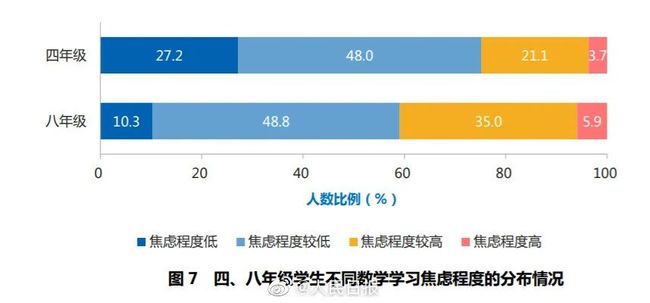
相信很多家长也深有感触,无论哪个学龄段的孩子,数学似乎都是个令人头疼的问题。
但是,数学的重要性不言而喻,如何激发孩子数学学习的内驱力?这是不少家长和教育工作者都在探寻的问题。
浏览了一众数学类教育资源网站后,外滩君发现,大部分国外网站普遍重视数学学习的趣味性,通过展现数学和实际生活的联系,或者环环相扣的逻辑推理,降低了孩子在学习数学过程中的枯燥感和困难。
因此,根据操作便捷度、内容质量、页面设计等多个因素,外滩君筛选出了8名“优胜选手”推荐给大家。
需要注意的是,不少网站的资源其实都跨越了多个年龄层,而不局限于外滩君介绍的某个年级。
因此,家长可以根据自身孩子的需求与能力挖掘更多、更适合的学习资料。
文章最后,外滩君还安排了一个彩蛋。数学天赋从何而来?数学历史上每一次精妙的推导、证明,依靠的都是从天而降的灵感吗?这些问题的答案,或许也决定了一个孩子在数学之路上究竟能走多远。
适合学前与幼儿园的孩子
“数学启蒙”是很多幼儿家长的关注重点。为了培养孩子的“数感”,家长们越来越早地开始教孩子数数。不过,有些家长已经发现,即使孩子能够流利地从1数到10,甚至100,让他拿5颗糖时,孩子依然会拿错。
这是因为,孩子只是像背诵字母一样记住了一首“数字歌”,没有建立起数字与数量的关系。事实上,理解这样一种关系更能促进孩子的数学能力发展。
美国儿童教育网站Starfall的数学教育就非常重视这一点。无论是数数、比较大小还是简单的运算,都会提供具象的水果、动物或者小朋友,帮助幼儿理解数字与数量的关系。

对于年龄较小的孩子,外滩君推荐Starfall中的“数学歌曲”板块。生动有趣的画面与歌唱的方式,更能吸引孩子的注意力,也符合他们的认知水平。
比如歌曲“十个孩子出来玩(Ten Kids Went to Play)”中,每出场一个孩子,身上都会带有相应的数字。

孩子在观看的过程中,更容易感受到数字与数量的对应关系。
对于年龄更大一些的孩子而言,学写数字可能是另一个难关。
而在英国中小学教材出版公司Twinkl的网站上,家长可以找到丰富的相关练习,下载或打印下来就能给孩子使用。
比如铅笔的控制练习、1-10的笔顺训练等等,其中同样包含数字与数量的关系,并且帮助孩子反复巩固每个数字的书写。

由于资源丰富、质量也有保障,很多当地和双语学校的老师都会从Twinkl下载海报、课堂练习等素材。
推荐网站1: Starfall
网址:https://www.starfall.com/h/
内容范围:英语阅读与口语、科学文化常识、数学......
适合年龄段:学前、幼儿园、小学低年级
使用权限:部分免费
推荐网站2: Twinkl
内容范围:文学、数学、音乐、科学等各学科、节日、健康教育、手工......
适合年龄段:学前、幼儿园、小学
使用权限:部分免费
*输入Offer code: USATWINKLHELPS 能下载更多免费资料,有效期至2020/4/13。
适合小学阶段的孩子
进入小学阶段,运算是数学学习的一个重头部分。不过动辄几十甚至几百道计算题,对孩子而言实在有些枯燥。
尤其涉及小数、分数的计算,孩子更感到复杂、不愿做题。
而网站Funbrain就有让孩子爱上数学的神奇魔力。
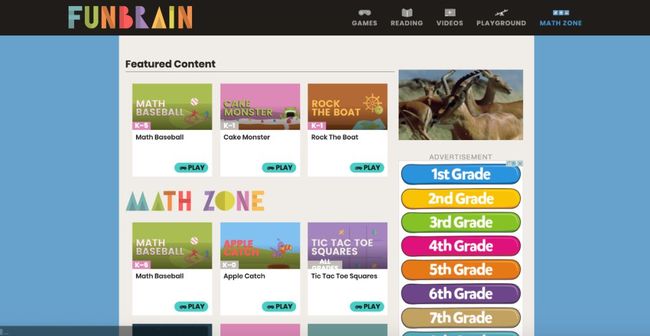
将小游戏与数学知识结合,整个画面看上去就很有吸引力。而且有些游戏还能选择难度,真正实现“玩中学”。
看懂游戏规则、琢磨玩法的过程也很能锻炼孩子的理解与运用能力。
比如在游戏“大黄蜂数字(Bumble Numbers)”中,孩子需要对花朵中的式子进行加法计算,然后控制画面中的蜜蜂抓取答案,再准确落到对应的花朵上。
同时,还要躲避过往的蜻蜓。因此,这个游戏还非常考验孩子的手眼协调能力与反映速度。

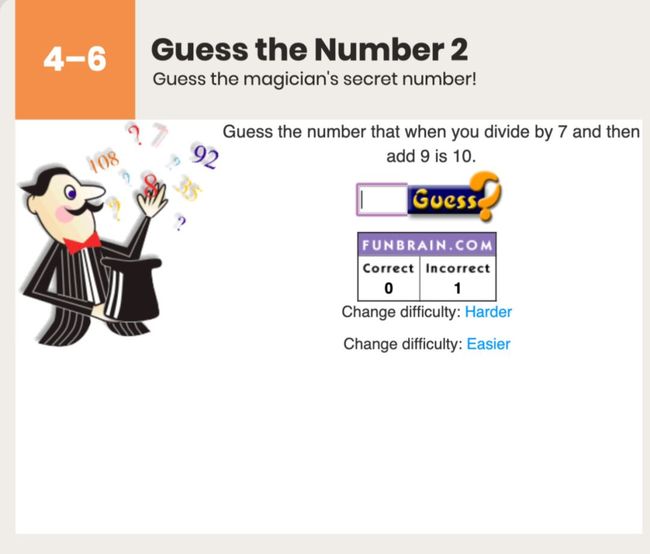
再如游戏“猜数字2(Guess the Number 2)”,孩子需要逆向推算出魔术师的神秘数字。这要求孩子不仅能熟练掌握四则混合运算,还要有一定的逆向思维能力。
如果输入的答案不正确,孩子会得到数字太大或太小的提示,还有相关计算过程。
除了运算能力,很多家长和教师反馈,应用题是孩子在小学阶段普遍遇到的一个难点,尤其是需要多步运算的应用题。
其中非常重要的原因之一是孩子审题能力弱,无法理解完整的题干信息,并且难以提炼出关键的数量关系。
对于这个问题,美国数学学习网站Zearn Math上提供了非常有针对性的教学视频和练习。

在视频中,老师会引导孩子阅读应用题题干,还会有互动环节,来帮助孩子思考和理解。虽然英文教学可能会带来一些障碍,但解题思路非常值得孩子学习,掌握后对日常中文应用题的练习也会有很大帮助。

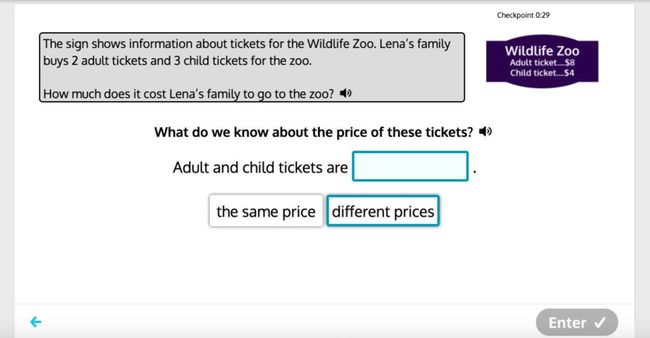
例题:动物园买票
推荐网站3: Funbrain
内容范围:数学、英文阅读
适合年龄段:幼儿园、小学
使用权限:免费
推荐网站4: Zearn
内容范围:数学
适合年龄段:幼儿园、小学
使用权限:免费
适合初中阶段的孩子
初中阶段的数学和小学相比,要跨上很高的一层台阶。
比如小学几何更偏向感性认知,图形的面积和体积计算也基本不会有太大问题,但到了初中,证明题的加入一下子提升了难度,需要孩子在掌握图形性质的基础上,还要能灵活运用。
针对初中几何的问题,外滩君首先想要推荐网站Twig Education,因为这个网站中的视频内容通常会将数学知识与实际生活联系在一起。
对于觉得几何学习有些困难的孩子而言,这样的内容更加直观有趣,不仅能消除孩子的畏难情绪,还能体会几何的巧妙。
比如在“三角形”的板块中,视频“建造金字塔”就将直角三角形的性质与埃及金字塔联系在一起。
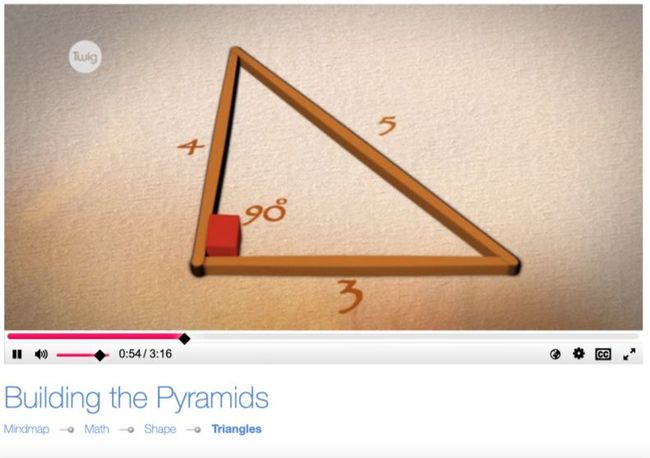
据视频介绍,建造金字塔时,为了确保底座是正方形而不是菱形,有一种说法是建筑师利用了边长比为3:4:5的三角形,因为这样的三角形一定是直角三角形,从而保证了金字塔底座的四个角一定是直角。
例如胡夫金字塔的底座,就是利用了边长分别为21、28和35的三角形,边长比同样是3:4:5。

而这个技巧,其实就包含了勾股定理的逆定理,这也是解证明题的常用定理之一。
如果说Twig Education是数学知识在现实生活中的运用,那么网站TeachingTextbooks所提供的内容更像是“会说话的教科书”。
比如同样关于三角形的知识,在一个类似书本的界面,Teaching Textbooks会有老师讲解全等三角形的性质与判定。

看完教学后,孩子可以点击配套习题进行练习,如果不会或做错了,同样有详细的解题步骤与老师讲解。
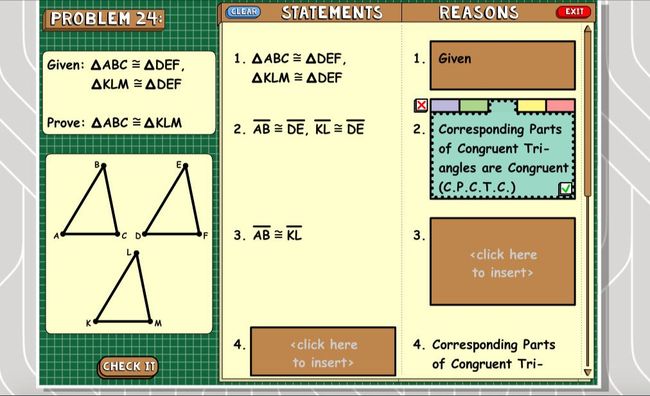
虽然是英文教学,但只要了解了数学术语的英文表达,配合题目和图片应该就不难理解。
推荐网站5: Twig Education
网址:https://www.go.twigeducation.com/covid19-us
内容范围:数学、科学、
适合年龄段:初中、高中
使用权限:注册后30天免费试用
推荐网站6: TeachingTextbooks
网址:https://www.teachingtextbooks.com/Default.htm
内容范围:数学
适合年龄段:小学、初中
使用权限:注册后试用部分内容,且永久有效
适合高中阶段的孩子
进入高中阶段,或者在初二、初三,部分走英国留学路线的学生就要开始GCSE和A Level的学习。
据了解,GCSE和A Level的数学虽然深度没有那么深,但是覆盖范围广。此外,全英文的数学题可能会让孩子感到不适应。
因此,做题、归纳总结、熟悉数学术语的英文表达可能是提升考试成绩的有效途径,而网站Seneca就提供了丰富的GCSE和A Level的数学学习资源,基本以幻灯片和互动题的形式出现。
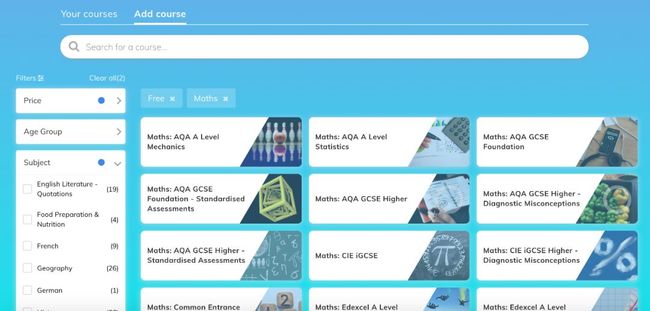
每道题目正确与否学生都能得到即时反馈。
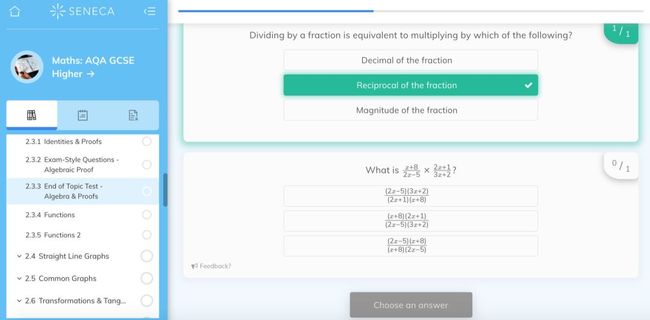
对于不计划赴英国留学的学生而言,如果对数学感兴趣,或者想提前学习大学相关内容,网站edX是一个不错的选择。
这个由麻省理工和哈佛联合创立的大规模在线课程平台,目前已经吸引了包括加州伯克利、牛津、清华、北大在内的多所世界名校提供课程。
因此,数学领域的课程涵盖范围更广,学生更易找到自己感兴趣的内容。
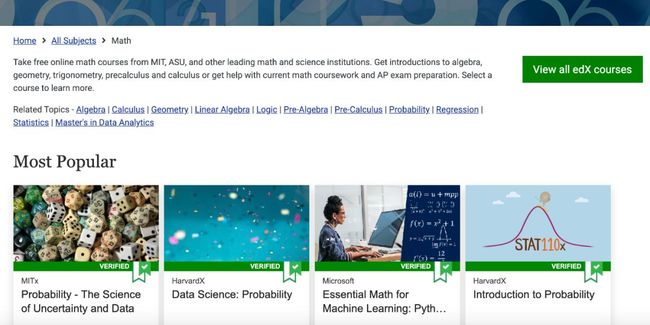
不仅如此,edX的数学课程中还包括了AP数学的教学资源。
比如很多参加AP考试的中国学生都会选择的AP微积分(考试分为AP微积分AB和AP微积分BC两个科目)
其中的微分方程和级数的内容,往往是考试的重难点所在。
而在edX上就有课程“AP微积分:微积分AB与微积分BC中具有挑战性的概念(AP Calculus: Challenging Concepts from Calculus AB & Calculus BC)”,完全针对学生普遍反映AP微积分中较难的内容展开,清晰流畅的视频讲解也非常适合高中生自学。
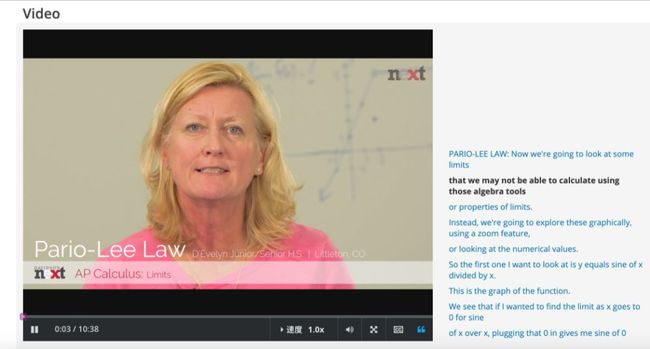
推荐网站7: Seneca
网址:https://www.senecalearning.com/
内容范围:全科,GCSE, A LEVEL
适合年龄段:初中、高中
使用权限:课程部分免费,教学材料全部免费
推荐网站8: edX
内容范围:各领域学科
适合年龄段:高中、大学
使用权限:教学视频免费,课后题收费
最后的彩蛋环节,外滩君想和大家分享哔哩哔哩网站上的一个视频,名叫《数学天赋是什么样的?它从何而来?(丹迪林双球)》(点击即可查看),由Up主3Blue1Brown 发布。
3Blue1Brown其实是一个由斯坦福大学的数学系学生Grant Sanderson创建的YouTube账号。通过演示动画解说高等数学,目前已经有259万位订阅者,并且火到了国内,而B站上的是这个频道的中国官方账号。

在这个视频中,Grant向观众介绍了自己最喜欢的数学证明之一,并借此探讨数学天赋与灵感的问题。
这道题目是,证明以下三种方式产生的曲线等价。
1.单个方向上伸缩圆
2.双图钉画法
3.斜切圆锥面

不难理解的是,这三种方式生成的都是椭圆,而它们也的确是椭圆的三个定义,但是如何证明呢?
如果感兴趣,不妨自己先思考一下。
Grant分享的是他在数学家保罗·洛克哈特所著的《度量》中,看到的一个巧妙的证明方法——在截面上下引入两个球体。


这两个球体分别在圆锥面相切于两个圆处,并且与截面相切于不同的点。
这个方法最早由杰米诺·皮埃尔·丹迪林与1822年提出,因此这两个球也被称为“丹迪林双球”。
后续的证明其实都不难,但球体的引入无疑是整个过程的“神来之笔”。


人们是怎样想出如此巧妙的证明的呢?
作者保罗猜测,这可能与《包法利夫人》和《蒙娜丽莎》等作品的诞生一样。“我不知道这样的构思是怎样出现的,我只知道当我有这种想法时,那就是上天的眷顾。”
这么说来,每次数学理论的发展,依靠的都是天赋以及从天而降的灵感吗?
Grant同意这个观点,但他更想深入分析一下。假设一个有着丰富几何解题经验的人面对这道证明题,他的思路是什么样的?
事实上,他的经验积累会让他非常熟悉线段“等长转化”的方法,从而更易联想到引入圆和球概念,因为它们的定义就包含了无数条等长线段,那么转化的可能性也就更高。

因此,Grant更想告诉观众的是:不要将这些天才般的技巧仅仅看作运气使然的奇迹,而要看作丰富阅历经验的结晶。
当你换个角度去思考时,就不再仅仅是佩服天才般的思想,而是会从中受到启发了。
不否认运气和天赋的因素,但更相信努力和积累的重要作用,并以兴趣为导向引导孩子学习数学,或许孩子也能因此拥有更多探索未知、迎难而上的动力。
关注外滩教育
阅读3000+篇优质文章
![]()
![]()











