目录
1. 线性模型
2. 线性回归
2.1 一元线性回归
3. 一元线性回归的Python实现
3.1 使用 stikit-learn
3.1.1 导入必要模块
3.1.2 使用 Pandas 加载数据
3.1.3 快速查看数据
3.1.4 使用 stlearn 创建模型
3.1.5 模型评估
3.2 手动实现
3.2.1 计算 w 和 b
3.2.2 功能封装
1. 线性模型
给定 dd 个属性描述的示例 x=(x1;x2;...;xd)x=(x1;x2;...;xd),其中 xixi 为 xx 在第 ii 个属性上的取值,线性模型(linear model)试图学得一个通过属性的线性组合来进行预测的函数,即:
f(x)=w1x1+w2x2+...+wdxd+b(1.1)(1.1)f(x)=w1x1+w2x2+...+wdxd+b
使用向量形式为:
f(x)=wTx+b(1.2)(1.2)f(x)=wTx+b
其中 w=(w1;w2;...;wd)w=(w1;w2;...;wd),表达了各属性在预测中的重要性。
2. 线性回归
给定数据集 D={(x1,y1),(x2,y2),...,(xm,ym)}D={(x1,y1),(x2,y2),...,(xm,ym)},其中 xi=(xi1;xi2;...;xid)xi=(xi1;xi2;...;xid),yi∈Ryi∈R。线性回归(linear regression)试图学得一个能尽可能准确地预测真实输出标记的线性模型,即:
f(xi)=wTxi+b,使得f(xi)≃yi(1.3)(1.3)f(xi)=wTxi+b,使得f(xi)≃yi
2.1 一元线性回归
先只考虑输入属性只有一个的情况,D={(x1,y1),(x2,y2),...,(xm,ym)}D={(x1,y1),(x2,y2),...,(xm,ym)},xi∈Rxi∈R。对离散属性,若属性值存在序(order)关系,可通过连续化将其转化为连续值。
如”高度“属性的取值“高”、“中”、“低”,可转化为{1.0,0.5,0.0}{1.0,0.5,0.0}。
若不存在序关系,则假定有 kk 种可能的属性值,将其转化为 kk 维向量。
如“瓜类”属性的取值有“冬瓜”、“西瓜”、“南瓜”,可转化为 (0,0,1),(0,1,0),(1,0,0)(0,0,1),(0,1,0),(1,0,0)。
线性回归试图学得:
f(xi)=wxi+b,使得f(xi)≃yi(1.4)(1.4)f(xi)=wxi+b,使得f(xi)≃yi
为使 f(xi)≃yif(xi)≃yi,即:使 f(x)f(x) 与 yy 之间的差别最小化。
考虑回归问题的常用性能度量——均方误差(亦称平方损失(square loss)),即让均方误差最小化:
(w∗,b∗)=arg min(w,b)∑i=1m(f(xi)−yi)2=arg min(w,b)∑i=1m(yi−wxi−b)2(1.5)(1.5)(w∗,b∗)=arg min(w,b)∑i=1m(f(xi)−yi)2=arg min(w,b)∑i=1m(yi−wxi−b)2
w∗,b∗w∗,b∗ 表示 ww 和 bb 的解。
均方误差对应了欧几里得距离,简称欧氏距离(Euclidean distance)。
基于均方误差最小化来进行模型求解的方法称为最小二乘法(least square method)。在线性回归中,就是试图找到一条直线,使得所有样本到直线上的欧氏距离之和最小。
下面需要求解 ww 和 bb 使得 E(w,b)=∑i=1m(yi−wxi−b)2E(w,b)=∑i=1m(yi−wxi−b)2 最小化,该求解过程称为线性回归模型的最小二乘参数估计(parameter estimation)。
E(w,b)E(w,b) 为关于 ww 和 bb 的凸函数,当它关于 ww 和 bb 的导数均为 00 时,得到 ww 和 bb 的最优解。将 E(w,b)E(w,b) 分别对 ww 和 bb 求导数得:
∂E(w,b)∂(w)=2(w∑i=1mx2i−∑i=1m(yi−b)xi)(1.6)(1.6)∂E(w,b)∂(w)=2(w∑i=1mxi2−∑i=1m(yi−b)xi)
∂E(w,b)∂(b)=2(mb−∑i=1m(yi−wxi))(1.7)(1.7)∂E(w,b)∂(b)=2(mb−∑i=1m(yi−wxi))
令式子 (1.6) 和 (1.7) 为 00 得到 ww 和 bb 的最优解的闭式(closed-form)解:
w=∑i=1myi(xi−x¯¯¯)∑i=1mx2i−1m(∑i=1mxi)2(1.8)(1.8)w=∑i=1myi(xi−x¯)∑i=1mxi2−1m(∑i=1mxi)2
b=1m∑i=1m(yi−wxi)(1.9)(1.9)b=1m∑i=1m(yi−wxi)
其中 x¯¯¯=1m∑i=1mxix¯=1m∑i=1mxi 为 xx 的均值。
3. 一元线性回归的Python实现
现有如下训练数据,我们希望通过分析披萨的直径与价格的线性关系,来预测任一直径的披萨的价格。

其中 Diameter 为披萨直径,单位为“英寸”;Price 为披萨价格,单位为“美元”。
3.1 使用 stikit-learn
3.1.1 导入必要模块
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
3.1.2 使用 Pandas 加载数据
pizza = pd.read_csv("pizza.csv", index_col='Id')
pizza.head() # 查看数据集的前5行

3.1.3 快速查看数据
我们可以使用 matplotlib 画出数据的散点图,x 轴表示披萨直径,y 轴表示披萨价格。
def runplt():
plt.figure()
plt.title("Pizza price plotted against diameter")
plt.xlabel('Diameter')
plt.ylabel('Price')
plt.grid(True)
plt.xlim(0, 25)
plt.ylim(0, 25)
return plt
dia = pizza.loc[:,'Diameter'].values
price = pizza.loc[:,'Price'].values
print(dia)
print(price)
plt = runplt()
plt.plot(dia, price, 'k.')
plt.show()
[ 6 8 10 14 18]
[ 7. 9. 13. 17.5 18. ]
3.1.4 使用 stlearn 创建模型
model = LinearRegression() # 创建模型
X = dia.reshape((-1,1))
y = price
model.fit(X, y) # 拟合
X2 = [[0], [25]] # 取两个预测值
y2 = model.predict(X2) # 进行预测
print(y2) # 查看预测值
plt = runplt()
plt.plot(dia, price, 'k.')
plt.plot(X2, y2, 'g-') # 画出拟合曲线
plt.show()
[ 1.96551724 26.37284483]
这里 fit()方法学得了一元线性回归模型 f(x)=wx+bf(x)=wx+b,这里 xx 指披萨的直径,f(x)f(x) 为预测的披萨的价格。
fit() 的第一个参数 X 为 shape(样本个数,属性个数) 的数组或矩阵类型的参数,代表输入空间;
第二个参数 y 为 shape(样本个数,) 的数组类型的参数,代表输出空间。
3.1.5 模型评估
成本函数(cost function)也叫损失函数(lost function),用来定义模型与观测值的误差。
模型预测的价格和训练集数据的差异称为训练误差(training error)也称残差(residuals)。
plt = runplt()
plt.plot(dia, price, 'k.')
plt.plot(X2, y2, 'g-')
# 画出残差
yr = model.predict(X)
for index, x in enumerate(X):
plt.plot([x, x], [y[index], yr[index]], 'r-')
plt.show()
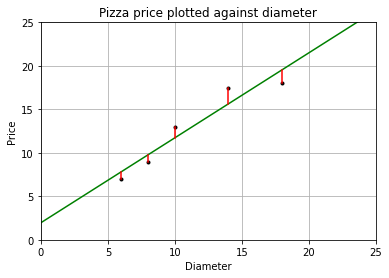
根据最小二乘法,要得到更高的性能,就是让均方误差最小化,而均方误差就是残差平方和的平均值。
print("均方误差为: %.2f" % np.mean((model.predict(X)-y) ** 2))
均方误差为: 1.75
3.2 手动实现
3.2.1 计算 w 和 b
ww 和 bb 的最优解的闭式(closed-form)解为:
w=∑i=1myi(xi−x¯¯¯)∑i=1mx2i−1m(∑i=1mxi)2(1.8)(1.8)w=∑i=1myi(xi−x¯)∑i=1mxi2−1m(∑i=1mxi)2
b=1m∑i=1m(yi−wxi)(1.9)(1.9)b=1m∑i=1m(yi−wxi)
其中 x¯¯¯=1m∑i=1mxix¯=1m∑i=1mxi 为 xx 的均值。
下面使用 Python 计算 ww 和 bb 的值:
w = np.sum(price * (dia - np.mean(dia))) / (np.sum(dia**2) - (1/dia.size) * (np.sum(dia))**2)
b = (1 / dia.size) * np.sum(price - w * dia)
print("w = %f\nb = %f" % (w, b))
y_pred = w * dia + b
plt = runplt()
plt.plot(dia, price, 'k.') # 样本点
plt.plot(dia, y_pred, 'b-') # 手动求出的线性回归模型
plt.plot(X2, y2, 'g-.') # 使用LinearRegression.fit()求出的模型
plt.show()
w = 0.976293
b = 1.965517
郑州妇科医院那家好:http://www.zzyytj.com/郑州妇科医院哪里好:http://www.zzyytj.com/郑州治疗妇科哪家医院好:http://www.zzyytj.com/
可以看到两条直线重合,我们求出的回归模型与使用库求出的回归模型相同。
3.2.2 功能封装
将上述代码封装成类:
class LinearRegression:
"""
拟合一元线性回归模型
Parameters
----------
x : shape 为(样本个数,)的 numpy.array
只有一个属性的数据集
y : shape 为(样本个数,)的 numpy.array
标记空间
Returns
-------
self : 返回 self 的实例.
"""
def __init__(self):
self.w = None
self.b = None
def fit(self, x, y):
self.w = np.sum(y * (x - np.mean(x))) / (np.sum(x**2) - (1/x.size) * (np.sum(x))**2)
self.b = (1 / x.size) * np.sum(y - self.w * x)
return self
def predict(self, x):
"""
使用该线性模型进行预测
Parameters
----------
x : 数值 或 shape 为(样本个数,)的 numpy.array
属性值
Returns
-------
C : 返回预测值
"""
return self.w * x + self.b
使用:
# 创建并拟合模型
model = LinearRegression()
model.fit(dia, price)
x2 = np.array([0, 25]) # 取两个预测值
y2 = model.predict(x2) # 进行预测
print(y2) # 查看预测值
runplt()
plt.plot(dia, price, 'b.')
plt.plot(x2, y2, 'y-') # 画出拟合
plt.show()
[ 1.96551724 26.37284483]