#树状数组(上) [TOC] 给出下一篇的链接:树状数组(下) ##简介 树状数组(Binary Indexed Tree)是一种修改和查询的时间复杂度都为$O(\log_2!n)$的一种数据结构。它支持查询区间和修改单点操作。 思想上，树状数组类似于线段树，还比线段树省空间，代码复杂度比线段树小，可以扩展到多维情况，不过适用范围比线段树小。 与线段树不同，树状数组在使用时无需建树，它的树状结构是数组模拟的。 ##结构分析 先看一张图：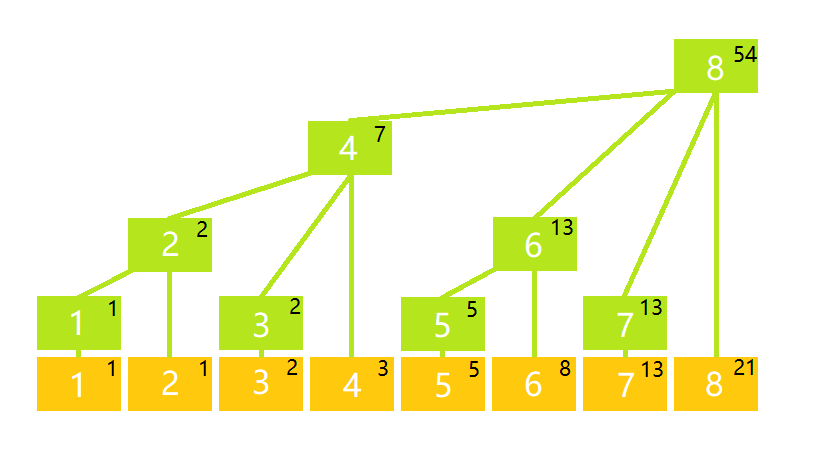 
这张图展示了树状数组的结构（想象出来的结构）。其中橙色代表原数组节点$A[i]$，绿色代表树状数组节点$C[i]$，每个节点右上角的数代表该节点的权值。你可以发现，每个绿色节点权值都等于其子节点权值和。 其中有两个重要的规律： \(C[i]=\sum_{j=i-\operatorname{lowbit}(i)+1}^{n}\!{A[j]}\qquad(1)\) \(\sum_{j=1}^{i}\!A[j]=C[i]+C[i-\operatorname{lowbit}(i)]+C[i-\operatorname{lowbit}(i)-\operatorname{lowbit}(i-\operatorname{lowbit}(i))]\cdots\qquad(2)\) 其中$i$为正整数。 在解释这两个规律之前，先来看看$\operatorname(i)$是啥。 ###lowbit函数 这是一种位运算黑科技，函数原型是$x$&$-x$。返回值是第一个小于等于$x$的$2^k(k为非负整数)$的数(从小到大枚举)。 举个例子，\(x=4\)，\(\operatorname{lowbit}(x)=4\)；\(x=7\)，\(\operatorname{lowbit}(x)=1\)。 如果没看懂还是百度一下吧 ###解释 ####对$(1)$式的解释： 对于$C[i]$，它对应$A[i-\operatorname(i)+1]+\cdots+A[i]$。 因此对$A[i]$加上$k$时，需要将每一个包含$A[i]$的$C[j]$加上$k$。 可以证明只有$C[i]$、\(C[i+\operatorname{lowbit}(i)]\)、$C[i+\operatorname(i)+\operatorname(i+\operatorname(i))]\cdots$包含$A[i]$。 举例：\(i=(6)_{10}=(110)_2\)，包含$A[i]$的$C[]$有$C[6]$、\(C[8]\)、$C[16]$等。 ####对$(2)$式的解释： 计算$A[1]+\cdots+A[i]$时，把$i$减去$\operatorname(i)$，得到新的$i_2$，再将$i_2$减去$\operatorname(i_2)$，以此类推，直到$i-\operatorname(i)$为$0$为止。 举例：\(i=(6)_{10}=(110)_2\)，\(A[1]+\cdots+A[6]=C[(110)_2]+C[(100)_2]=C[6]+C[4]=13+7=20\)。 下面看看树状数组的基本操作“单点修改”和“区间查询”是如何实现的。 ##操作与变式 ###单点修改 在原数组中$A[i]$的位置加上一个值，并维护树状数组。 根据上文对$(1)$式的解释，可得如下代码：
inline void add(int x,int k)//维护树状数组C，对应于原数组A的操作就是A[i]+=k
{
for(;x<=n;x+=x&-x)//x & -x 就是lowbit()函数
c[x]+=k;
}
###区间查询 计算$A[1]+\cdots+A[i]$。 根据上文对$(2)$式的解释，可得如下代码：
inline int ask(int x)//查询A[1]+···+A[x]的值
{
int ans=0;
for(;x;x-=x&-x)
ans+=c[x];
return ans;
}
如果上文的解释你没看懂，可以体会一下这两段代码。 ###区间修改，单点查询 这里利用了差分的思想（似乎是差分最广泛的应用） 我们发现，当$A[l]~A[j]$都加上一个值时，相邻的A[i]之差不变。 这启发我们利用差分进行变式，使其支持单点查询和区间修改操作。 可以用树状数组维护原数组的差分数组。 举例：A[]={1,2,3,5}，B[]={1,1,1,2}，C[]={1,2,1,5}。 ###区间修改，区间查询 我们知道，“区间修改，区间查询”的操作本质上是用树状数组$C[]$维护原数组$A[]$的差分数组$B[]$，因此若要查询区间，时间复杂度是$O(n!\log_2!n)$的。 有没有改进的方法？ 根据差分的性质$A[x]=\sum_i^x B[i]$可得 \(\sum_{i=1}^x A[i]=\sum_{i=1}^x\sum_{j=1}^i B[j]\) 等式右边可以转化： \(\sum_{i=1}^x\sum_{j=1}^i B[j]\) \(=B[1]+(B[1]+B[2])+\cdots+(B[1]+\cdots+B[x])\) \(=\sum_{i=1}^{x}(x+1-i)\times B[i]\) \(=(x+1)\times\sum_{i=1}^{x}B[i]-\sum_{i=1}^{x}(i\times B[i])\) 可以发现，这个式子的第一项能通过区间查询树状数组$tree[]\(算出（区间查询\)[1,x]$，乘$x+1$）；第二项可以用一个新的树状数组（设为$tree2[]$）维护$i\times B[i]$即可。 根据上文，我们可对$\operatorname()\(函数与\)\operatorname()$函数作一些改动：
long long tree[N],tree2[N],a[N],n,m;
//注意add()与ask()的改动
inline void add(long long x,long long k)//给x加上k
{
for(long long x0=x;x<=n;x+=x&-x)
tree[x]+=k,tree2[x]+=k*x0;
}
inline long long ask(long long x)//查询[1,x]权值和
{
long long ans=0;
for(long long x1=x+1;x;x-=x&-x)
ans+=x1*tree[x]-tree2[x];
return ans;
}
修改区间[l,r]：add(l,k),add(r+1,-k) 查询区间[l,r]：ask(r)-ask(l-1) 当然，也可以用原来的函数，不作改动，这种方式的代码可以看看lpf_666的文章（强烈推荐） ###二维树状数组 既然有二维前缀和，自然就会有二维树状数组： 利用树状数组的思想维护一个$A[N][M]$的二维数组。 代码实现并不复杂，与之前的情况类似，只是多了一层循环：
const int N=10005;
const int M=10005;
int tree[N][M],a[N][M],n,m;
inline void add(int x,int y,int k)//修改操作，相当于A[x][y]+=k
{
//这里的for循环不能用之前的写法，否则会出错，想想为什么
for(int i=x;i<=n;i+=i&-i)
for(int j=y;j<=m;j+=j&-j)
tree[i][j]+=k;
}
inline int ask(int x,int y)//查询A[1][1]至A[x][y]的一个子矩阵和
{
int ans=0;
for(int i=x;i;i-=i&-i)
for(int j=y;j;j-=j&-j)
ans+=tree[i][j];
}
类似地，二维树状数组也可以利用差分进行变式，从而实现其他功能。 若已经看懂了之前的部分，读者可以尝试自己实现一下。 ##模板 ###LG3304【模板】树状数组 1 模板题，上代码
#include
using namespace std;
int n,m,a[1000005],tr[1000005];
inline void add(int x,int y)
{
for(;x<=n;x+=x&-x)
tr[x]+=y;
}
inline int ask(int x)
{
int ans=0;
for(;x;x-=x&-x)
ans+=tr[x];
return ans;
}
int main()
{
ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=1,w;i<=n;i++)
{
scanf("%d",&a[i]);add(i,a[i]);
}
for(int i=1,t,x,y;i<=m;i++)
{
scanf("%d%d%d",&t,&x,&y);
if(t==1) add(x,y);
else printf("%d",ask(y)-ask(x-1));
}
return 0;
}
###LG3368【模板】树状数组 2
//在实际操作时其实可以一边读入一边计算差分
#include
#include
#include
using namespace std;
long long a[500005],tr[500005],n,m;
inline void add(long long x,long long k)
{
for(;x<=n;x+=x&-x)
tr[x]+=k;
}
inline long long ask(long long x)
{
int ans=0;
for(;x;x-=x&-x)
ans+=tr[x];
return ans;
}
int main()
{
long long t,x,y,k;
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
add(i,a[i]-a[i-1]);//a[i]-a[i-1]是差分的定义
}
while(m--)
{
cin>>t;
if(t==1)
{
scanf("%lld%lld%lld",&x,&y,&k);
add(x,k),add(y+1,-k);//差分的性质1:区间[l,r]的元素加k，在原数组要依次维护区间
//[l,r]中的每一个元素，在差分数组只要使b[l]+k，b[r]-k
//即可
}
else
{
scanf("%lld",&x);
printf("%lld\n",ask(x));//差分的性质2:A[i]=B[1]+···+B[i]
}
}
return 0;
}
###A Simple Problem with Integers 区间修改，区间查询：
#include
#define N 100005
using namespace std;
long long tree[N],tree2[N],a[N],n,m;
inline void add(long long x,long long k)
{
for(long long x0=x;x<=n;x+=x&-x)
tree[x]+=k,tree2[x]+=k*x0;
}
inline long long ask(long long x)
{
long long ans=0;
for(long long x1=x+1;x;x-=x&-x)
ans+=x1*tree[x]-tree2[x];
return ans;
}
int main()
{
ios::sync_with_stdio(false);
cin>>n>>m;
char c;
for(long long i=1;i<=n;i++)
cin>>a[i],add(i,a[i]-a[i-1]);
for(long long i=1,t,l,r,k;i<=m;i++)
{
cin>>c>>l>>r;
if(c=='C') cin>>k,add(l,k),add(r+1,-k);
if(c=='Q') cout< ###LG4054[JSOI2009计数问题] 二维树状数组模板，不过这里维护的是一个子矩阵中某种特定权值出现的个数，修改操作是改变一个格子的权值。 可以发现权值范围不大（$1\leq\leq 100$），因此设立$tree[c][x][y]$表示$c$在矩阵A[1][1]至A[x][y]中出现了几次： 代码如下：
#include
#include
#include
using namespace std;
int tree[101][301][301],a[301][301],n,m,q;
int oper,X1,X2,Y1,Y2,c;
inline void add(int c,int x,int y,int k)
{
for(int i=x;i<=n;i+=i&-i)
for(int j=y;j<=n;j+=j&-j)
tree[c][i][j]+=k;
}
inline long long ask(int c,int x,int y)
{
long long ans=0;
for(int i=x;i;i-=i&-i)
for(int j=y;j;j-=j&-j)
ans+=tree[c][i][j];
return ans;
}
int main()
{
ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[i][j],add(a[i][j],i,j,1);
cin>>q;
while(q--)
{
cin>>oper;
if(oper==1)
{
cin>>X1>>Y1>>c;
add(a[X1][Y1],X1,Y1,-1);
a[X1][Y1]=c;
add(c,X1,Y1,1);
}
else
{
cin>>X1>>X2>>Y1>>Y2>>c;
cout< ##结语 树状数组还是蛮神奇的，跟线段树比起来，算法常数小，代码短，省空间 敬请期待$树状数组(下)$ \(\xrightarrow{\qquad}To\;be\;continued\cdots\)