基于均值坐标(Mean-Value Coordinates)的图像融合算法的具体实现

1. 概述

泊松融合是图像融合处理效果最好的算法，其来自于2004年Siggraph的经典paper：《Poisson Image Editing》。以这篇文章为发端，很多大神提出了一系列的优化算法。2009年, Zeev Farbman 在的SIGGRAPH上面提出的基于Mean-Value Coordinates方法的泊松融合加速算法《Coordinates for Instant Image Cloning》（文献二）。在这篇文章中，泊松方程被转换成拉普拉斯方程，并且提出了用均值坐标Mean-Value Coordinates来近似求解这个方程，从而达到实时运算的效果。

初步了解了一下原生的泊松融合算法和均值坐标融合算法，其原理包含的内涵十分丰富，包含一些诸如列散度、拉普拉斯算子、梯度场、泊松方程等等数学知识，要完全弄明白确实需要一定的基础。这里就重点关注一下根据《Coordinates for Instant Image Cloning》（文献二）实现图像融合的过程，有机会的话再详细推导一下其原理。

2. 实现

2.1. 准备

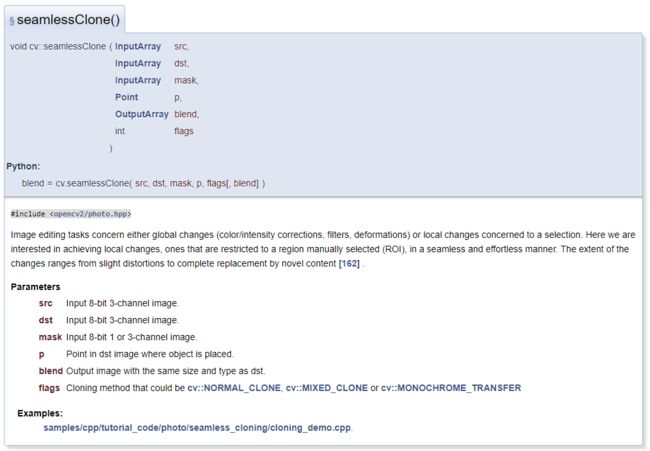
在OpenCV中，已经收录了泊松融合算法，也就是函数seamlessClone()：

这个算法要求输入一个源图像，一个目标图像，源图像希望融合到目标图像的位置，以及一个mask图像。这个mask图像也就是一张二值化图像，用来标识图像的ROI(region of interest感兴趣区域)。均值坐标融合算法的输入参数也是一样的，不过mask图像很难以处理，OpenCV自带的GUI难以满足需求。所以我这里通过QT来做GUI，通过OpenCV将图像显示到QT窗体上，然后再QT窗体的图像区域内绘制多边形，多边形内部即为ROI。可以参考我的这两篇文章：
《使用QT显示OpenCV读取的图片》
《使用QT绘制一个多边形》

2.2. 核心

2.2.1. 均值坐标（Mean-Value Coordinates）

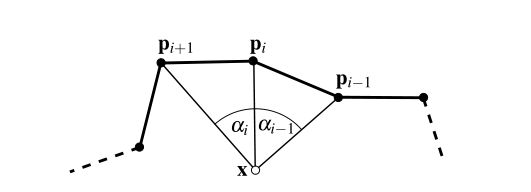
在论文中提出了一个很重要的概念也就是均值坐标（Mean-Value Coordinates）。对于如下多边形内部的点：

都有一系列与多边形边界相关的坐标值：

也就是说，只要确定了ROI，也就确定了ROI区域内每个点的均值坐标（Mean-Value Coordinates），每个点会有m个值（m为ROI边界多边形的顶点）。

2.2.2. ROI边界栅格化

论文中是以ROI边界多边形为例的，实际用到图像处理中是不会只用几个多边形的节点来计算的，而应该是ROI边界上连续的点。实际上不用想也知道，图像融合最关键的部分就是ROI边界部分的像素值。必须要用到ROI边界上所有的像素值来计算。

也就是说这里还需要一个工作，就是将ROI边界多边形栅格化，取得其上连续的像素位置，得到准确的栅格化多边形边界。这里可以参看我的这篇文章《矢量线的一种栅格化算法》。按照顺序逐条将多边形的边栅格化，即可以得到ROI的栅格化多边形边界。

2.2.3. 核心实现

论文给出的算法伪代码如下：

这段算法描述并不复杂，转换成自然语言如下：

1. 假设ROI区域内有n个点，其边界由m个点组成。
2. 那么可以求每个点的MVC(均值坐标)，每个点有m个坐标值，一共有n个点，MVC就是就是一个n*m的矩阵。
3. 求ROI区域边界的像素差diff，显然其是一个m*1的矩阵。
4. 那么新图像ROI区域的插值为：r = MVC * diff，矩阵乘法后r为n*1矩阵。
5. 将插值r与原图像g矩阵相加：f = g + r，替换目标图像相应位置的值。

核心部分具体的实现代码如下：

    QTime startTime = QTime::currentTime();

    //Step1:找到边界上所有的像素点
    vector ROIBoundPointList;
    CalBoundPoint(ROIBoundPointList);

    //Step2:计算范围内每个点的 mean-value coordinates
    size_t srcImgBufNum = static_cast(srcImg.cols) * static_cast(srcImg.rows);
    vector> MVC(srcImgBufNum);
    for(size_t i = 0; i < srcImgBufNum; i++)
    {
        MVC[i].resize(ROIBoundPointList.size()-1, 0);
    }
    vector clipMap(srcImgBufNum, true);           //标识范围内的点

    cout<<"开始计算 mean-value coordinates..." << endl;
    #pragma omp parallel for        //开启OpenMP并行加速
    for (int ri = 0; ri < srcImg.rows; ++ri)
    {
        for (int ci = 0; ci < srcImg.cols; ++ci)
        {
            //点是否在多边形内
            size_t m = static_cast(srcImg.cols) * ri + ci;
            if(!Point_In_Polygon_2D(ci, ri, ROIBoundPointList))
            {
                clipMap[m] = false;
                continue;
            }

            //逐点计算MVC
            Vector2d P(ci, ri);
            vector alphaAngle(ROIBoundPointList.size());
            for(size_t pi = 1; pi < ROIBoundPointList.size(); pi++)
            {
                alphaAngle[pi] = threePointCalAngle(ROIBoundPointList[pi-1], P, ROIBoundPointList[pi]);
            }
            alphaAngle[0] = alphaAngle[ROIBoundPointList.size()-1];


            for(size_t pi = 1; pi < ROIBoundPointList.size(); pi++)
            {
                double w_a = tan(alphaAngle[pi-1]/2) + tan(alphaAngle[pi]/2);
                double w_b = (ROIBoundPointList[pi-1] - P).Mod();
                MVC[m][pi-1] = w_a / w_b;
                if(_isnan(MVC[m][pi-1])==1)
                {
                    MVC[m][pi-1] = 0;
                }
            }

            double sum = 0;
            for(size_t pi = 0; pi < MVC[m].size(); pi++)
            {
                sum = sum + MVC[m][pi];
            }

            for(size_t pi = 0; pi < MVC[m].size(); pi++)
            {
                MVC[m][pi] = MVC[m][pi] / sum;
            }
        }
    }
    cout<<"计算完成！" << endl;

    //Step3:计算边界的像素插值
    vector diff;
    for(size_t i = 0; i < ROIBoundPointList.size()-1; i++)
    {
        size_t l = (size_t) srcImg.cols * ROIBoundPointList[i].y + ROIBoundPointList[i].x;
        for(int bi = 0; bi < winBandNum; bi++)
        {
            size_t m = (size_t) dstImg.cols * winBandNum * (ROIBoundPointList[i].y + posY)+ winBandNum * (ROIBoundPointList[i].x + posX) + bi;
            size_t n = (size_t) srcImg.cols * winBandNum * ROIBoundPointList[i].y + winBandNum * ROIBoundPointList[i].x + bi;
            int d = (int)(dstImg.data[m]) - (int)(srcImg.data[n]);
            diff.push_back(d);
        }
        clipMap[l] = false;         //在多边形边上的点没法计算MVC
    }

    //Step4:插值计算
    cout<<"开始插值计算..." << endl;
    //Mat rMat(srcImg.rows, srcImg.cols, CV_64FC3);
    #pragma omp parallel for
    for (int ri = 0; ri < srcImg.rows; ++ri)
    {
        for (int ci = 0; ci < srcImg.cols; ++ci)
        {
            size_t l = (size_t) srcImg.cols * ri + ci;
            if(!clipMap[l])
            {
                continue;
            }

            vector r(winBandNum, 0);

            for(size_t pi = 0; pi < MVC[l].size(); pi++)
            {
                for(int bi = 0; bi < winBandNum; bi++)
                {
                    r[bi] = r[bi] + MVC[l][pi] * diff[pi * winBandNum + bi];
                }
            }

            for(int bi = 0; bi < winBandNum; bi++)
            {
                size_t n = (size_t) srcImg.cols * winBandNum * ri + winBandNum * ci + bi;
                size_t m = (size_t) dstImg.cols * winBandNum * (ri + posY)+ winBandNum * (ci + posX) + bi;

                dstImg.data[m] = min(max(srcImg.data[n] + r[bi], 0.0), 255.0);
            }
        }
    }
    cout<<"插值完成！" << endl;

    QTime stopTime = QTime::currentTime();
    int elapsed = startTime.msecsTo(stopTime);
    cout<<"总结完成用时"<

2.2.4. 实现中的问题

1. ROI边界上的点无法计算MVC值，需要予以剔除，否则ROI边界上会出现一圈白色的点。
2. 用到了OpenMP加速，可以大幅提高性能。如有必要的话，可以通过显卡加速。

3. 效果

3.1. 使用过程

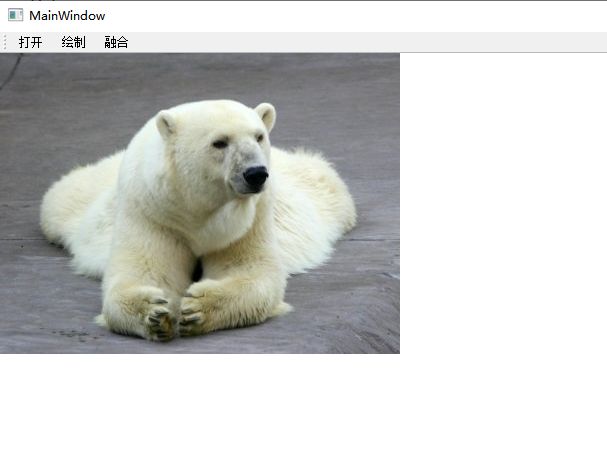
程序源代码可参见文章最末的链接，是一个OpenCV结合QT的GUI的程序。编译运行后，点击"打开"按钮，界面会显示源图像：

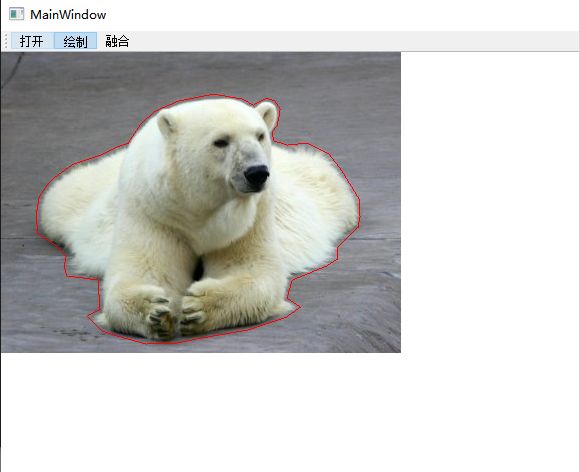
点击"绘制"按钮，在源图像区域内绘制一个多边形，确定一个ROI：

准备一张想要融合的目标图像：

点击"融合"按钮，会加载目标图像，并会根据设置的位置，将源图像的ROI融合到目标图像中：

3.2. 效率

在Debug模式，不使用OpenMP加速的情况下，这个算法的效率大约需要50秒左右的时间。

在Debug模式，使用OpenMP加速，算法的效率可以优化到10秒，也就是不使用OpenMP加速时的5倍左右。而我使用的机器CPU是i7-8750H标压6核CPU，考虑到一些IO操作造成的性能损耗，这个优化效率是正常的。

最后在使用Release模式，使用OpenMP加速之后，算法的效率可以优化到1秒左右，这说明编译器优化对程序性能也是有很大影响的，尤其是对并行程序而言。

这个实现只是这个算法的初始实现，效率就已经达到了1秒左右，看来论文说的可以达到实时融合确实不是虚言。有机会再尝试一下论文中提到的一些性能优化实现。

4. 参考

[1] 泊松融合及其优化算法
[2] Coordinates for Instant Image Cloning
[3] 图像处理（十二）图像融合(1)Seamless cloning泊松克隆-Siggraph 2004
[4] 多尺度并行坐标插值实时图像克隆算法

实现代码