方差分析

方差分析的主要功能就是验证两组样本，或者两组以上的样本均值是否有显著性差异（是否一致）。

这里有两个大点需要注意：①方差分析的原假设是：样本不存在显著性差异（即，均值完全相等）；②两样本数据无交互作用（即，样本数据独立）这一点在双因素方差分析中判断两因素是否独立时用。

原理

方差分析的原理就一个方程：SST=SSM+SSE   (全部平方和=模型平方和+误差平方和)

方差分析看的最终结果看的统计量是：F统计量、R²。

F=[SS_M/(S-1)]/[SS_E/(N-S)]   S水平个数，S-1模型只有度，N-S误差自由度。

R²=SS_M/SS_T   

方差分析步骤：

①建立原假设和备泽假设，原假设为：不同水平对应均值相等；

②给定那个显著水平α，默认0.05；

③计算F统计量的F₀值（F₀=误差自由度/模型自由度）。

方差假设条件为残差服从正态分布，其条件等价于：

①每组观测服从正态分布（观测数目足够多就认为正态分布）；

②方差齐性；

③数据中的观测间独立。

可用于方差分析的三个过程步：TTEST、ANOVA、GLM分别适用于一个因素两个水平(TTEST\ANOVA\GLM)、一个因素多个水平(ANOVA\GLM)、多个因素(ANOVA\GLM)。不同的是ANOVA适用于处理均衡数据（每个分类观测数量相等）。

DATA RELIEFTIME;
    INPUT MEDICINE $ HOURS @@;
    DATALINES;
    A 7 A 5 A 3 A 1
    B 6 B 5 B 5 B 3
    C 7 C 9 C 8 C 9
    D 4 D 4 D 3 D 3
    ;
RUN;
PROC ANOVA DATA=RELIEFTIME;
    CLASS MEDICINE;
    MODEL HOURS=MEDICINE;
RUN;

注：进行此分析有一个大前提，是在假设方差分析的三个条件都满足的前提下！

此处MEDICINE是影响的因素，因素中包含多个水平，HOURS是相应变量。

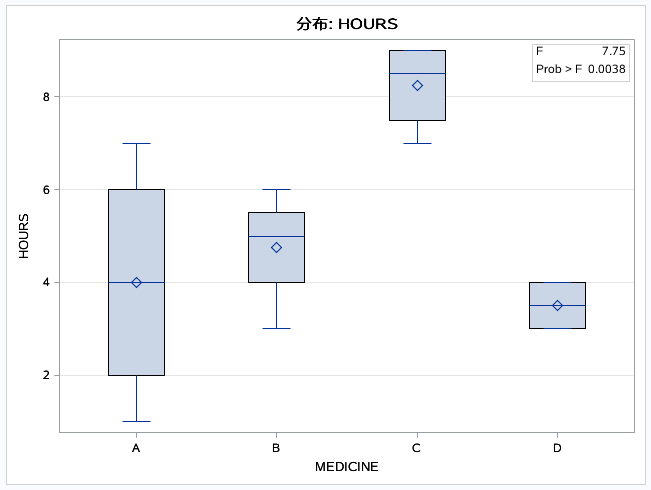
结果如下图：

先统计有多少个水平，多少个观测；

由上图第一张表得知：模型自由度为3，误差自由度为12，拟合的合计自由度为15。F₀=4，即当模型平方和=误差平方和时F=4，而在第一张表中F=7.75说明SS_M/SS_E>1所以在P值允许的情况下该因素的不同水平之间是存在显著差异的。而进一步看P值，看出F值有效，即得出结论，该药物对缓解时间有显著性影响。

在进一步看盒形图，也能得出C水平药物与其他的有明显差异。

以下来介绍GLM过程步

该过程步可以对正态性条件和方差齐性条件进行验证，实则方便许多。

PROC GLM DATA=RELIEFTIME PLOTS(ONLY)=DIAGNOSTICS;
    CLASS MEDICINE;
    MODEL HOURS=MEDICINE;
    MEANS MEDICINE/HOVTEST;
RUN;

先看该数据是否满足条件进行方差分析，

其残差是已经满足正态分布的，看Q-Q图也可以看出大致分布在直线两侧，所以数据是满足正态性条件的；

上图是齐方差性检验，看P>0.05，所以满足齐方差性的假设，即满足的方差齐性条件。

同时该题假设各组观测数据是独立的。

接下来看方差分析结果：

从第二张表F=7.75说明在模型平方和占比显著，说明数据值有效。进而因为P<0.05所以拒绝原假设，不同水平之间存在显著差异。

同时看第三张表R方>0.5说明数据模型平方和占比显著。

在看最后两张表，有两种平方和的计算方法，因为是单因素分析，所以不同方法求得的值相同，一般情况下我们默认看Ⅲ型平方和数据，和之前的数据是一样的。

LSMEANS语句

GLM过程步中有LSMEANS语句（LSMEANS 因素<选项>）进行水平的差异分析，选项可用来控制误差，若要控制两两比较的误差则用 LSMEANS/PDIFF=ALL ADJUST=T,

若重点控制正果实验过程中的误差则用  LSMEANS/PDIFF=ALL ADJUST=TUKEY(此选项仅考虑两两比较的情形) 或者 LSMEANS/PDIFF=CONTROL('控制组') ADJUST=DUNNETT。

PROC GLM DATA=RELIEFTIME PLOTS(ONLY)=DIAGNOSTICS;
    CLASS MEDICINE;
    MODEL HOURS=MEDICINE;
    LSMEANS MEDICINE/PDIFF=ALL;
RUN;

即如果如下：

第一张表是表明不同水平于1234的对应关系，

第二张表可以看出M_{12 、}M_14、M24、M43、M24的P>0.05所以我们接受原假设量水平见无显著差异，但是其余的就有显著差异了。

双因素方差检验

双因素甚至多因素方差检验多看了一个因素之间的交互性除了各个因素分别看差异之外，还有因素1*因素2合起来的水平之间的差异性，如下代码：

PROC GLM DATA=SASHELP.CLASS;
    CLASS AGE SEX;
    MODEL WEIGHT= AGE SEX AGE*SEX;
RUN;

与单因素方差分析的结果相比不一样的结果如下：

注：前面提到的原假设是因素间各自独立，没有交互作用。所以看交互因素AGE*SEX的P>0.05所以原假设成立，两因素没有交互作用。所以两因素各自分开看即可。

同时从表中可以看到只有AGE一个显著因素，所以后面加上语句LSMEANS AGE/PDIFF=ALL ADJUST=TUKEY

PROC GLM DATA=SASHELP.CLASS;
    CLASS AGE SEX;
    MODEL WEIGHT= AGE SEX AGE*SEX;
    LSMEANS AGE/PDIFF=ALL ADJUST=TUKEY;

RUN;

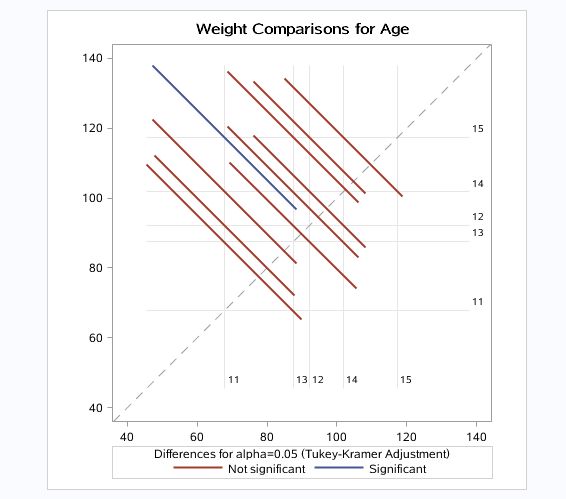
多出结果；

该图为年龄对体重的影响的置信区间图，对角线为组间差异的参考先（0线），与改线相交说明两水平均值没有显著差异，

所以有意义的线只有一条蓝线（11岁和15岁差异性比较显著）。

接下来看一个因素间有交互作用的例子，

PROC GLM DATA=FRUIT;
    CLASS HUMIDITY TEMPERATURE;
    MODEL OUTPUT_LBS=HUMIDITY TEMPERATURE HUMIDITY*TEMPERATURE;
    LSMEANS HUMIDITY*TEMPERATURE/SLICE=HUMIDITY;
RUN;

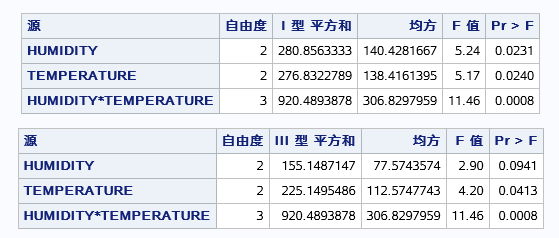
之前运行过一遍不加LSMEANS HUMIDITY*TEMPERATURE/SLICE=HUMIDITY;语句的，结果看到：

HUMIDITY*TEMPERATURE无交互作用的假设被拒绝了，说明有交互作用，所以加上LSMEANS HUMIDITY*TEMPERATURE/SLICE=TEMPERATURE;

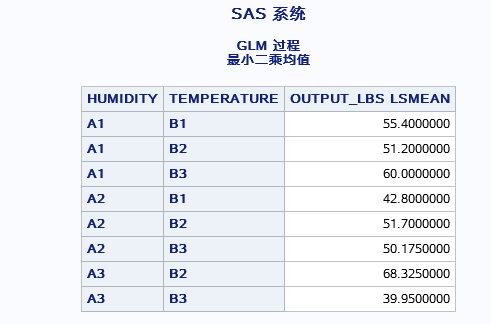
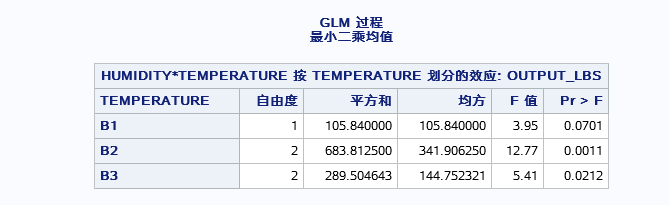
看交互因素的不同水平间的影响，并且因素TEMPERATURE是显著因素，HUMIDITY是不显著因素，（这里两因素交互对植物生长影响是显著的，可是单单温度对植物生长没有显著影响，所以这里可以看当湿度为什么情况下，温度才会起显著作用。）所以，SLICE选项功能是从那个温度角度出发看不同温度下不同湿度对生长情况的影响你。结果如下图：

结果就是温度为B2、B3情况下，湿度对植物生长具有显著影响。（注：方差分析原假设为均值相等，即无差别）