如果文章可以帮助到您,这是我写文章的荣幸。
这篇文章您可以了解到:
- 二叉树的各种遍历方法的简单解释
- 遍历方法的递归和循环的python3代码实现
对应的代码位于这里
二叉树的各种遍历方法的简单解释
二叉树顾名思义,最多两个孩子。
一般规定一个二叉树,因为节点间有相互连接的原因,所以只要给定根节点,那么顺着寻找左孩子和右孩子便可以遍历到所有的节点,这就是遍历的直观解释。
而遍历分为深度遍历和广度遍历(具体叫法我没有考证,大家也没有必要太深究一个名字本身,含义更重要是吧 ^.^ ),深度遍历类似于深度搜索的顺序,是深度优先遍历的循序。而广度遍历类似于广度搜索的顺序,是广度优先遍历的循序。我是从这方面区分的,为什么这么分类的原因在之后递归和遍历实现的时候就更能体现这个原因了。
具体看下图:
* 前序遍历:根节点 -> 左子树 -> 右子树
* 中序遍历:左子树 -> 根节点 -> 右子树
* 后序遍历:左子树 -> 右子树 -> 根节点
* 层次遍历:第一层,第二层,...
遍历方法的递归和循环的python代码实现
1.1. 递归方式的前序遍历
使用递归的方式很容易理解:
先排除空节点,然后操作节点,然后左子树同样操作,右子树同样操作
简单解释一下,递归需要有终止条件,也就是空节点的时候。而且对于前序遍历的具体节点的遍历顺序需要明确知道——根节点,根节点的左孩子,然后是左孩子的左孩子,直到没有左孩子,然后是右孩子,然后是右孩子的左孩子...这么描述很难理解,所以之后有例子。
代码实现:
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def preorderTraversal(root: TreeNode):
if root is None:
return
# do something here, e.g. print itself
print(root.val)
preorderTraversal(root.left)
preorderTraversal(root.right)
很简单,其中的类“TreeNode”的代码之后不再赘述。需要运行一下
if __name__ == '__main__':
root=TreeNode(1)
root.left=TreeNode(2)
root.right=TreeNode(3)
root.left.left=TreeNode(4)
root.left.right=TreeNode(5)
root.right.left=TreeNode(6)
root.left.left.right=TreeNode(7)
preorderTraversal(root)
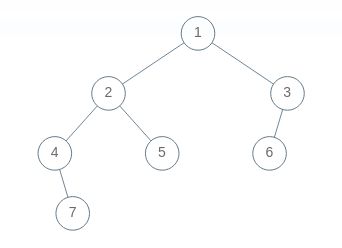
这个就是这样一个二叉树:
输出是这样的:
1
2
4
7
5
3
6
遍历顺序看图体会一下。
1.2.循环方式的前序遍历
这里插上一句,循环本身和递归是表达的同样一个算法核心,所以呢,不要过于恐惧循环的写法,而且不要太希望递归修改成循环会有很大的速度提升。
我们首先需要处理根节点,然后是根节点的左子树,那么之后处理根节点的右子树的话,我们就需要事先储存根节点,方便之后需要右子树,同理,每一个节点都需要如此操作。而且我们完全处理完一个左子树之后,我们紧接着需要这个左子树的父节点,那么就是最近存储的节点。综上,我们需要的操作是储存节点,而储存的容器是栈,因为后进先出。
为了统一化这种方法(递归转化为循环),规则化一些内容:将现在的节点计算出其他节点称为:,对于现在的节点的执行称为:,而在栈中的数据是该节点和是否被扩展过。
所以流程就是:
- 初始化时将根节点加入栈,标记未扩展
- 进行循环,直到栈空
- 循环中,取出节点。先判断节点非空,如果标记为未扩展,那么扩展左右孩子加入栈中,先加右孩子,然后是左孩子(因为我们希望的循序是根->左->右,而我们使用的是栈),都标记为未扩展,最后是本节点,标记为扩展;如果标记为扩展,那么进行操作
可能你会学过其他的前序循环的写法,会发现将第三步中这个节点标记是没有意义的,不使用标记一样可以实现(因为这个是一种尾递归的缘由,就是递归部分在操作之后),这没错,但是之后中序后序遍历的时候就要吃苦头了。
按照流程我们编写程序:
def preorderTraversal(root: TreeNode):
stack=[(root,False)]
while len(stack)>0:
tree,extend=stack.pop()
if tree is None:
continue
if not extend:
stack.append((tree.right,False))
stack.append((tree.left,False))
stack.append((tree,True))
else:
# do something here, e.g. print itself
print(tree.val)
当然可以舍弃扩展概念(笔者不推荐):
def preorderTraversal(root: TreeNode):
stack=[root]
while len(stack)>0:
tree=stack.pop()
if tree is None:
continue
stack.append(tree.right)
stack.append(tree.left)
# do something here, e.g. print itself
print(tree.val)
2.1. 递归方式的中序遍历
def inorderTraversal(root: TreeNode):
if root is None:
return
inorderTraversal(root.left)
# do something here, e.g. print itself
print(root.val)
inorderTraversal(root.right)
2.2.循环方式的中序遍历
和之前及其相似,中序后序上的理解和写法的也是很简单的
def inorderTraversal(root: TreeNode):
stack=[(root,False)]
while len(stack)>0:
tree,extend=stack.pop()
if tree is None:
continue
if not extend:
stack.append((tree.right,False))
stack.append((tree,True))
stack.append((tree.left,False))
else:
# do something here, e.g. print itself
print(tree.val)
3.1. 递归方式的后序遍历
def postorderTraversal(root: TreeNode):
if root is None:
return
postorderTraversal(root.left)
postorderTraversal(root.right)
# do something here, e.g. print itself
print(root.val)
3.2.循环方式的后序遍历
def postorderTraversal(root: TreeNode):
stack=[(root,False)]
while len(stack)>0:
tree,extend=stack.pop()
if tree is None:
continue
if not extend:
stack.append((tree,True))
stack.append((tree.right,False))
stack.append((tree.left,False))
else:
# do something here, e.g. print itself
print(tree.val)
3. 层次遍历
这个层次遍历有点特殊,之前的分类中它被分为广度遍历中,因为这个遍历是一层一层的,也就是说,如果使用循环表示的话,它的结构不像栈,而像队列,需要先进先出。
对于递归和循环的转换上,我主张的是递归一定可以转换成循环,而循环不一定能转换成递归,而递归有一种解决到底然后再解决其他问题的特点,也就是深度,需要使用对应循环写法中的栈,这些讨论之后我会出一篇文章仔细讨论,这里提一提,如果认为有兴趣的话,可以关注我一下,这一星期我就会写那一篇。
所以呢,我没有找到层次遍历递归的方法,就算存在这样的方法,也不是很必要,毕竟已经失去递归的简单直观的特点。
所以流程就是:
- 初始化时将根节点加入队列
- 进行循环,直到队列空
- 循环中,取出节点。先判断节点非空,扩展左右孩子加入栈中,先加左孩子,然后是右孩子,并且进行该节点的操作
这个流程相对简单,有点像前序遍历的简单写法
def levelOrderTraversal(root: TreeNode):
stack=[root]
while len(stack)>0:
tree=stack.pop(0)
if tree is None:
continue
stack.append(tree.left)
stack.append(tree.right)
# do something here, e.g. print itself
print(tree.val)
推荐
leetcode中文
leetcode:二叉树的前序遍历
leetcode:二叉树的中序遍历
leetcode:二叉树的层次遍历
5.我的github
5.这篇文章对应的代码
注释
[1]:“现在的节点计算出其他节点称为:扩展[1]”:为什么叫做扩展,是因为节点到其他节点,其他节点的数量可能是多个,也可能是1个,也可能是0个,所以扩展合适一些