基于python的神经网络与机器学习

---

姓名：张博奇
学号：2014301020063
班级：物基一班

---

摘要：本文利用BP算法思想构建二层神经网络和更复杂的三层神经网络，训练神经网络根据输入数据集预测输出数据，对神经网络的结构有了初步的认识，阐述了权重矩阵（网络参数）在神经网络中的核心作用。并在此基础上用三层神经网络训练机器学习分类器，进而预测正确的分类，并讨论隐藏层维度对分类结果的大致影响。

关键词：神经网络、预测、机器学习、权重矩阵

引言

机器学习，是如今最令人振奋的计算机领域之一。国际著名的互联网公司，诸如Google、Facebook、Apple、Amazon早已展开了一场关于机器学习的军备竞赛。从手机上的语音助手、垃圾邮件过滤到逛淘宝时的物品推荐，无一不用到机器学习技术。2016年在围棋界大放异彩的AlphaGo也是机器学习的成功案例。

背景知识

在20世纪下半叶，机器学习作为人工智能的子领域诞生了，其目标是通过自学习算法从数据中获取知识，然后对未来世界进行预测。无需借助人力从数据中得到规则，机器学习能够自动建立模型进行预测。
机器学习是从对大脑的工作原理的研究逐步发展起来的。Warren McCullock和Walter Pitts 在1943年首次提出了一个简化版大脑细胞的概念，即McCullock-Pitts(MCP)神经元(W.S.McCulloch and W.Pitts. A Logical Calculus of the IdeasImmanent in Nervous Activity.)。

神经元是大脑中内部连接的神经细胞，作用是处理和传播化学和电信号。McCullock和Pitts描述了如下的神经细胞：可以看做带有两个输出的简单逻辑门；即有多个输入传递到树突（Dentrity），然后在神经元（Cell nucleus）内部进行输入整合，如果累积的信号量超过某个阈值，会产生一个输出信号并且通过轴突（Axon）进行传递。十几年后，基于MCP神经元模型，Frank Rosenblatt发表了第一个感知机学习规则(F.Rosenblatt, The Perceptron, a Perceiving and Recognizing Automaton. Cornell Aeronautical Laboratory, 1957)。基于此感知机规则，Rosenblatt提出了能够自动学习最优权重参数的算法，权重即输入特征的系数。后文中会有具体阐述。

构建二层神经网络

BP算法，即误差反向传播（Error Back Propagation, BP）算法。BP算法的基本思想是，学习过程由信号的正向传播与误差的反向传播两个过程组成。由于多层前馈网络的训练经常采用误差反向传播算法，人们也常把将多层前馈网络直接称为BP网络。

下面尝试着用BP算法训练的神经网络根据输入数据预测输出数据。从二层神经开始入手，输入X和输出Y数据集均以矩阵的形式给出。每一行代表一个训练样本（即相当于对大脑施加一次刺激），每一列代表一个输入结点（即相当于接受刺激的部位）。l0和l1分别代表输入网络层和中间隐藏层，显然有数据集X等于输入网络层l0。syn0表示连接l0和l1层的突触，也即上文提到的权重。
取4次训练样本[0,0,1],[0,1,1],[1,0,1],[1,1,1]和拟定的输出结果[0,0,1,1].T代码如下：

import numpy as np
 
# sigmoid 函数
def nonlin(x,deriv=False):
    if(deriv==True):
        return x*(1-x)
    return 1/(1+np.exp(-x))
 
# 输入数据集
X = np.array([  [0,0,1],
                [0,1,1],
                [1,0,1],
                [1,1,1] ])
 
# 输出数据集            
y = np.array([[0,0,1,1]]).T
 
np.random.seed(1)
 
# 随机初始化权重并使均值为零
syn0 = 2*np.random.random((3,1)) - 1
 
for i in range(10000):
    l0 = X
    l1 = nonlin(np.dot(l0,syn0))

#误差
    l1_error = y - l1
 
    l1_delta = l1_error * nonlin(l1,True)
 
# 更新权重
    syn0 += np.dot(l0.T,l1_delta)
print (l1)

点击查看代码
输出结果为：
[[ 0.00966449]
[ 0.00786506]
[ 0.99358898]
[ 0.99211957]]
从输出结果可以看出，其值与每个训练样本第一个结点的值是相近的，但第二与第三个结点的作用使得输出结果有偏差。我们成功地利用输入的训练样本预测了输出。
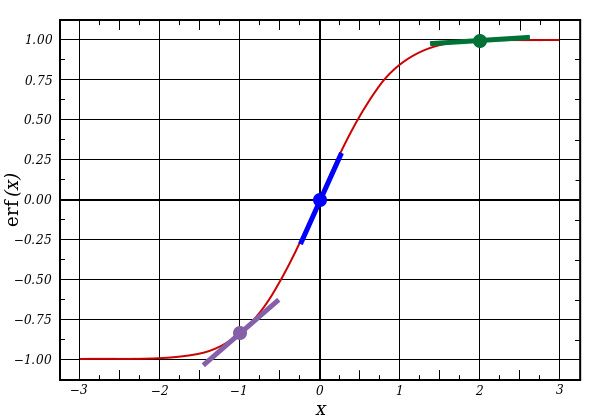
其中，Sigmoid 函数

可以将任何值都映射到一个位于 0 到 1 范围内的值。通过它，我们可以将实数转化为概率值。通过 “nonlin” 函数体还能得到 sigmod 函数的导数（当形参 deriv 为 True 时）。由于Sigmoid函数是非线性的，允许我们拟合非线性假设，类似的函数还有tanh、ReLUs等。
权重syn0是随机生成的一个3行一列矩阵，与输入X相乘后得到一个数值，经过nolin函数作用后得到对应的概率值，也就是猜测结果。l1_error则评估预测值l1与初始设定的Y值差值。nolin函数形参 deriv 为 True 时得到Sigmoid 函数导数。

由上图可以看出导数值在X绝对值较大时很小，在X绝对值较小时很大，但可以计算其导数值始终小于1。这个特性导致l1绝对值很大时其nolin函数值很小，l1_error相乘是一个较小值；l1绝对值很小时其nolin函数值很大，l1_error相乘是一个较大值。从统计学角度而言，我们对较为确定的事件赋予小的权重，对不确定的事件赋予大的权重。将nolin函数值乘上误差时，实际上就在以高确信度减小预测误差，更新权重后得到更进一步的准确的权重值。从这里我们就可以看出，神经网络的训练过程，实际上就是对一个随机权重不断训练，最后使输入数据集在权重的作用下越来越接近输出值的过程。神经网络是基于输入与输出间的联系进行学习的。

构建三层神经网络

在构建二层神经网络时，我们将输出数据集定为[0,0,1,1].T，但是如果我们将输出数据集改为[0,1,1,0].T，重新执行上述代码，可以发现输出的l1为：
[[ 0.5]
[ 0.5]
[ 0.5]
[ 0.5]]
这和我们的拟定输出数据集不一致，神经网络并没有按照输入与输出间的关系预测输出值。这是因为不一定总是单个输入与输出间存在一对一的关系，也可能是两个输入对应一个输出，甚至更复杂。输入与输出不一定是呈线性相关。或者说，输入的组合与输出间存在着一对一的关系。
为了解决这种更复杂的对应关系，需要额外增加一个网络层。第一层对输入进行组合，然后以第一层的输出作为输入，通过第二层的映射得到最终的输出结果。通过增加更多的中间层，以对更多关系的组合进行建模。这一策略正是人们所熟知的“深度学习”。
三层神经网络中，l0作为输入层，l1作为中间隐藏层，l2作为输出层。增加l2层和连接l1与l2间的权重syn1，并使l1_error等于l2误差更新值乘权重（这种做法也称作“贡献度加权误差”），可以写出三层神经网络的代码：

import numpy as np

# sigmoid 函数 
def nonlin(x,deriv=False):
    if(deriv==True):
        return x*(1-x) 
    return 1/(1+np.exp(-x))

# 输入数据集 
X = np.array([[0,0,1],
            [0,1,1],
            [1,0,1],
            [1,1,1]])

# 输出数据集 
y = np.array([[0],
            [1],
            [1],
            [0]])
 
np.random.seed(1)
 
# 随机初始化权重并使均值为零
syn0 = 2*np.random.random((3,5)) - 1
syn1 = 2*np.random.random((5,1)) - 1
 
for j in range(50000):
    l0 = X
    l1 = nonlin(np.dot(l0,syn0))
    l2 = nonlin(np.dot(l1,syn1))
 
#l2层
    l2_error = y - l2 
    l2_delta = l2_error*nonlin(l2,deriv=True)
    
#l1层 
    l1_error = l2_delta.dot(syn1.T) 
    l1_delta = l1_error * nonlin(l1,deriv=True)
    
# 更新权重
    syn1 += l1.T.dot(l2_delta)
    syn0 += l0.T.dot(l1_delta)
print(l2)

点击查看代码
输出结果为：
[[ 0.00248611]
[ 0.99693818]
[ 0.99597714]
[ 0.00503275]]
可见已经较好的得到了与拟定输出结果相近的预测值。三层神经网络构建成功。

利用三层神经网络预测分类

• 产生数据集
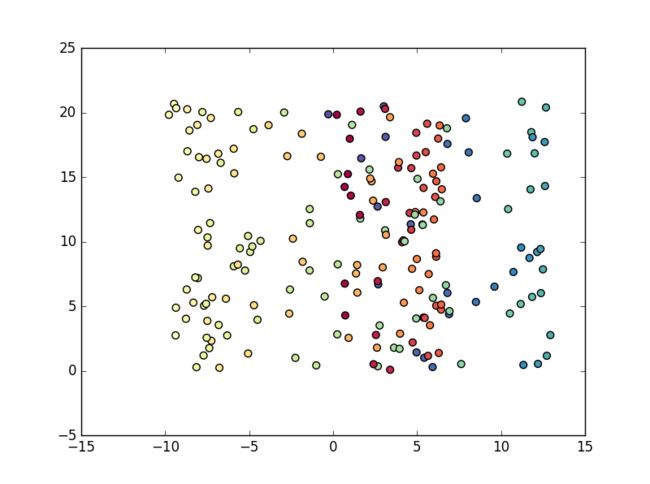
  利用scikit-learn可以产生很多有趣的数据集。

  
  
  

  swiss_roll
  
  
  

  circle
  
  

  这里采用整体较好分辨又具有一定难度分辨全部数据集的半月形数据集。

moons

• 构建三层神经网络并训练机器学习分类器
  由于图形是弯曲的，我们无法直接画一条直线以区分红点与蓝点这两类数据。因此需要构建一个具有输入层、隐藏层、输出层的三层神经网络来分辨。由于是二维图像，输入结点选择为两个，两类需要分辨的数据，输出结点也选择为两个。隐藏层的结点数不是固定的，比如在上文构建三层神经网络中选择了（5×1）矩阵，也就是五结点数（五维）隐藏层。结点数对数据筛选的影响会在后面讨论。
  zi是输入层、ai是输出层。W1,b1,W2,b2是需要从训练数据中学习的网络参数，也就是上文提到的权重（矩阵）。依然选择sigmoid函数在z1与a1间进行映射，z2与a2间则采用Softmax函数进行映射（Softmax函数也是转化成概率的一种方法，关于Softmax函数可查看维基百科）。
  向前传播进行预测：

为了找到使误差函数最小时权重W1,b1,W2,b2的值，可以使用梯度下降方法，这里采用有固定学习速率的批量梯度下降法。梯度下降需要一个与参数相关的损失函数的梯度。先定义：

与参数相关的损失函数的梯度:

利用后向传播导数实现批量梯度下降，进而更新网络参数W1,b1,W2,b2，减小误差。

• 对数据集进行分类
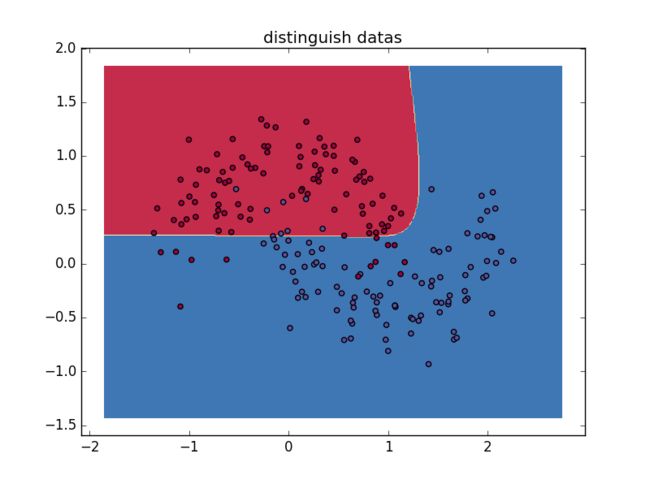
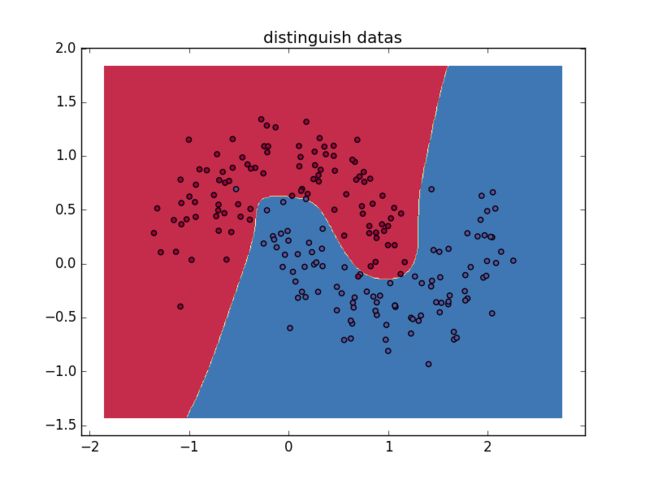
  运行程序，最终实现了将半月形中蓝色数据集与红色数据集分离：

  
  
  

点击查看源代码
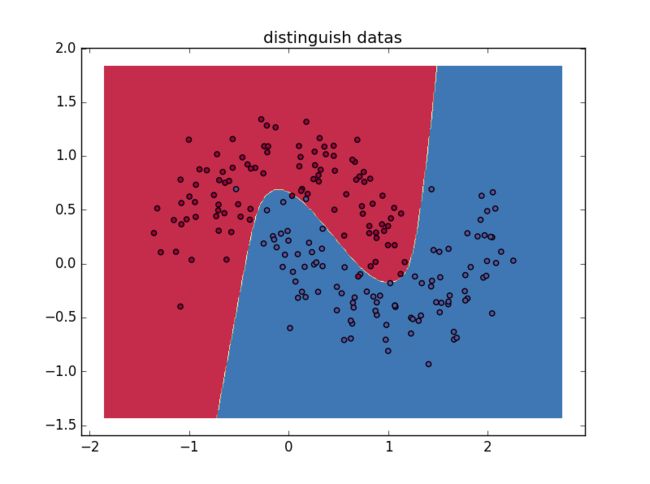
可以看出绝大多数红色数据集与蓝色数据集实现了分离，只有极少数数据集被分在了错误的位置，神经网络能够找到成功区分不同数据集的决策边界，数据集的分类获得成功。下面改变隐藏层维度，来评估不同隐藏层维度会对数据分离结果造成的影响：

隐藏层为一维

隐藏层为二维

隐藏层为五维

隐藏层为十维

隐藏层为五十维

可以看出隐藏层为一维时相当于线性分割两种数据集，随着维度增加分割效果得到提高，在隐藏层达到十维时只有一个本方数据集被排除在外，分割效果最好，隐藏层增加到五十维时没有明显的变化，这就需要改进算法实现更优的数据筛选效果，包括采用其他的层间映射函数、更有效的梯度计算方法（显然有固定学习速率的批量梯度下降法不是最高效的方法）、更多层次的神经网络等。

结论

一个基本的三层神经网络由输入层、隐藏层、输出层构成，相邻两层间由权重矩阵（网络参数）连接。通过不断提供训练样本，神经网络会学习最优权重参数，从而减小误差，利用输入数据建立模型并模拟输出。输入层与输出层结点数、隐藏层维度、层间映射函数、梯度计算方法都会对神经网络的准确性造成影响。本文仅对神经网络与机器学习做了基于个人能力的粗浅分析，更具有生产力的神经网络远比本文所述复杂。相信随着科技的发展，未来人工智能会丰富每个人的生活！

致谢

Python机器学习
Implementing a Neural Network from Scratch in Python – An Introduction
Computational Physics, Nicholas J.Giordano, Hisao Nakanishi