在这个目录下面的上一篇文章里面写了，对于一个数据集，如何用逻辑回归的方式去给他们分类。（链接 ： http://www.jianshu.com/p/5ae1399a512b）同样对于这个数据集，这篇文章写的是用一个神经网络的方式去给他们分类。
写在前面
对于下面关于神经网络的公式推导和计算的符号表示，我参考的是吴恩达的deeplearning 的视频里面的符号表示。如果看不懂的话，可以去cousera上或网易云课堂上面看它的课程。
对于神经网络，有很多现成的框架和库，可以很方便的帮助你使用。但是我这几篇文章的想法都是自己去实现这个网络，不用框架和库函数。对于一个初学者，我认为这样有助于我理解这个网络的细节。
在实现的过程中，我尽可能的使用了向量化的方式去实现矩阵计算。虽然被老是被矩阵的维度搞昏，当这应该是一个好习惯。向量化的矩阵计算，不仅可以计算的更快，而且还提高了代码的可读性。
神经网络的结构
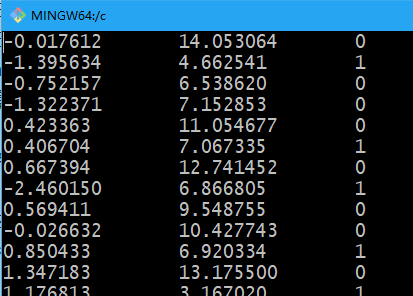
数据集的结构，如下图，（第一列和第二列表示对应的输入，第三列表示输出）：
image.png
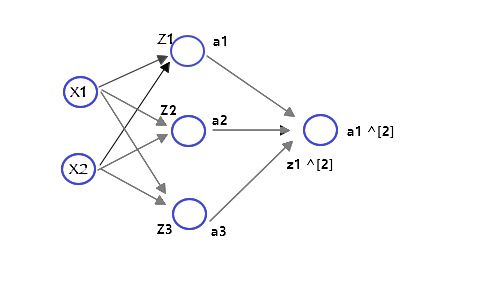
设计的网络的结构如下：
image.png
PS :
z1，z2，z3 画图的时候，这里有一点错误，应该写成z11，z12，z13
第一个1表示是第一层的输入，第二个1，2，3表示的是第一层的第一个，第二个，第三个结点
z1^[2] ,应该写成z21，表示的是第二层的第一个结点的输入，a1^[2] 表示的是第二层第一个节点的输出
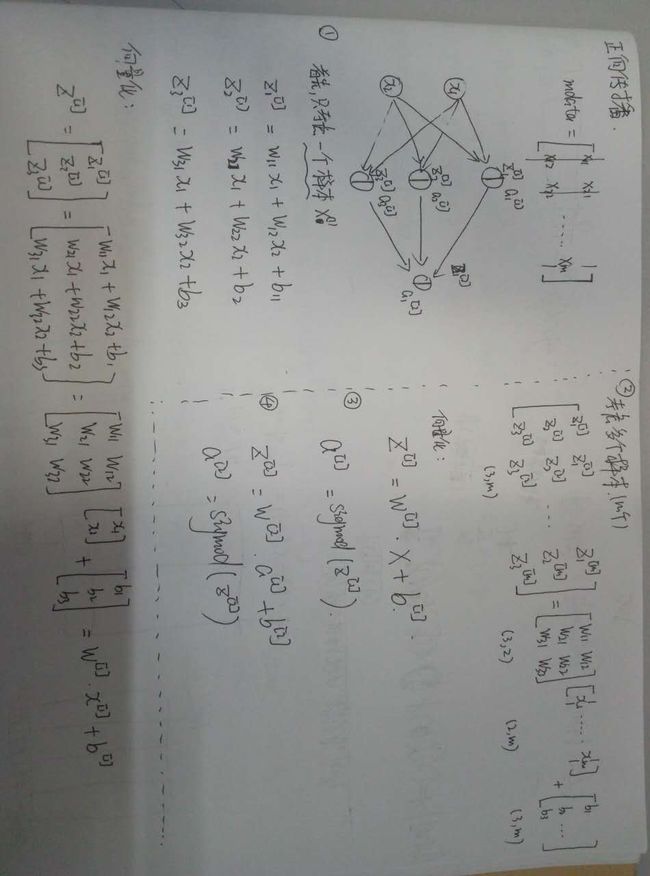
推理过程
微信图片_20170914152329.jpg
微信图片_20170914152509.jpg
源码
"""
实现一个三层的神经网络
一个输入层，一个输出层，隐层有3个结点
数据集同样也是tesetSet的数据集，和逻辑回归的数据集是同一个，格式如下：
x1 x2 y
-0.017612 14.053064 0
....
"""
import numpy as np
from numpy import random
import matplotlib.pyplot as plt
alpha=0.01
#加载数据集，原来的数据在文件排列是按行排列
#为了计算需要，将原来的数据加载到了矩阵之后，给矩阵装置了，是数据变成按列排列
def loadDataset():
data=[]
label=[]
f=open("textSet.txt")
for line in f:
lineArr=line.strip().split()
data.append( [float(lineArr[0]),float(lineArr[1]) ] )
label.append(float(lineArr[2]))
mdata=np.array(data)
mlabel=np.array(label)
return mdata.T,mlabel.T
def sigmod(inX):
return 1.0/(1+np.exp(-inX))
#激活函数的倒数
def sigmod_diff(inX):
return sigmod(inX) * (1-sigmod(inX))
def get_z1(inputs,mlabel,weights_layer1,b1,weights_layer2,b2):
z1=np.dot(weights_layer1,inputs)+b1
return z1
def get_a1(inputs,mlabel,weights_layer1,b1,weights_layer2,b2):
z1=np.dot(weights_layer1,inputs)+b1
a1=sigmod(z1)
return a1
def forward(inputs,mlabel,weights_layer1,b1,weights_layer2,b2):
#从输入层到隐层
z1=np.dot(weights_layer1,inputs)+b1
a1=sigmod(z1)
#从隐层到输出层
z2=np.dot(weights_layer2,a1)+b2
a2=sigmod(z2)
#error
dz2=a2-mlabel
return dz2
#计算cost，每一次迭代之后，都算一下cost，看看cost是否在减小
def cost(inputs,mlabel,weights_layer1,b1,weights_layer2,b2):
nx,m=inputs.shape
#从输入层到隐层
z1=np.dot(weights_layer1,inputs)+b1
a1=sigmod(z1)
#从隐层到输出层
z2=np.dot(weights_layer2,a1)+b2
a2=sigmod(z2)
#cost
cost=-mlabel* np.log(a2)-(a2-mlabel)*np.log(1-a2)
return np.sum(cost)/m
#将训练的输出和真实的结果show出来
def show1(inputs,mlabel,weights_layer1,b1,weights_layer2,b2):
nx,m=inputs.shape
#从输入层到隐层
z1=np.dot(weights_layer1,inputs)+b1
a1=sigmod(z1)
#从隐层到输出层
z2=np.dot(weights_layer2,a1)+b2
a2=sigmod(z2)
plt.plot(mlabel)
plt.plot(a2[0])
plt.show()
def show2(inputs,mlabel,weights_layer1,b1,weights_layer2,b2):
nx,m=inputs.shape
#从输入层到隐层
z1=np.dot(weights_layer1,inputs)+b1
a1=sigmod(z1)
#从隐层到输出层
z2=np.dot(weights_layer2,a1)+b2
a2=sigmod(z2)
new_a2=[]
for i in a2[0]:
#这里用0.1和0.9，是为了避免和mlabel画出来的线重合
if i <0.5:
new_a2.append(0.1)
if i>=0.5:
new_a2.append(0.9)
plt.plot(mlabel)
plt.plot(new_a2)
plt.show()
#正向传播和反向传播
def gradientdesc(mdata,mlabel,weights_layer1,b1,weights_layer2,b2):
nx,m=mdata.shape
#调用正向传播的函数，得到dz2
dz2=forward(mdata,mlabel,weights_layer1,b1,weights_layer2,b2)
#求dw2和db2
a1=get_a1(mdata,mlabel,weights_layer1,b1,weights_layer2,b2)
dw2 = (1/float(m)) * np.dot(dz2,a1.T)
db2 = (1/float(m)) * np.sum(dz2)
#求dw1和db1
z1=get_z1(mdata,mlabel,weights_layer1,b1,weights_layer2,b2)
dz1 =np.dot(weights_layer2.T,dz2) * sigmod_diff(z1)
dw1 = (1/float(m)) * np.dot(dz1,mdata.T)
db1 = (1/float(m)) * np.sum(dz1)
#更新w1,w2,b1,b2
weights_layer1=weights_layer1 - alpha * dw1
weights_layer2=weights_layer2 - alpha * dw2
b1=b1-alpha*db1
b2=b2-alpha*db2
return weights_layer1,b1,weights_layer2,b2
def three_layer_nn(maxcycle=5000):
mdata,mlabel=loadDataset()
nx,m=mdata.shape
hiden_node=3
#随机初始化 权值矩阵
weights_layer1=random.random(size=(hiden_node,nx))
b1=random.random(size=(hiden_node,m))
weights_layer2=random.random(size=(1,hiden_node))
b2=random.random(size=(1,m))
#迭代
for i in range(maxcycle):
weights_layer1,b1,weights_layer2,b2=gradientdesc(mdata,mlabel,weights_layer1,b1,weights_layer2,b2)
print (cost(mdata,mlabel,weights_layer1,b1,weights_layer2,b2))
#show
show2(mdata,mlabel,weights_layer1,b1,weights_layer2,b2)
if __name__=='__main__':
maxcycle=15000
three_layer_nn(maxcycle)
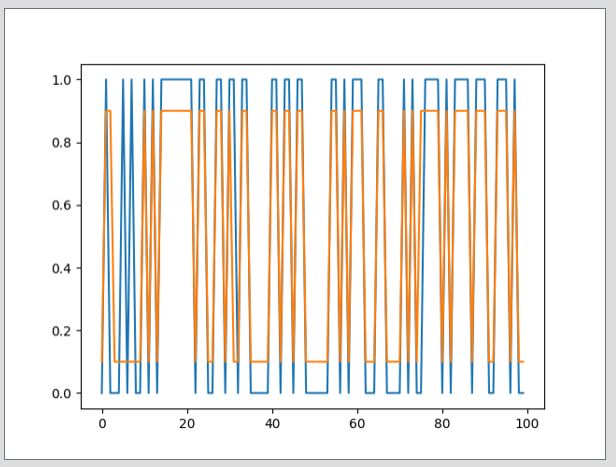
运行的结果：
（ps：黄色的线是预测的输出，为了黄色和蓝色不覆盖，我把黄色的输出应该是为1的改成了0.9，应该是为0的改成了0.1）
image.png
git链接：
数据集和代码都在里面 https://github.com/zhaozhengcoder/Machine-Learning/tree/master/three-layer-nn