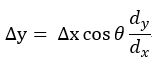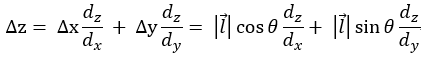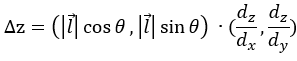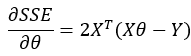梯度下降法原理以及代码实现
本篇博客承接本人上一篇关于逐步回归算法的引申,本篇将开始整理梯度下降算法的相关知识。梯度下降,gradient descent(之后将简称GD),是一种通过迭代找最优的方式一步步找到损失函数最小值的算法,基本算法思路可总结为如下几点:
(1) 随机设置一个初始值
(2) 计算损失函数的梯度
(3) 设置步长,步长的长短将会决定梯度下降的速度和准确度,之后会详细展开
(4) 将初值减去步长乘以梯度,更新初值,然后将这一过程不断迭代
1. 原理讲解——二维平面情形
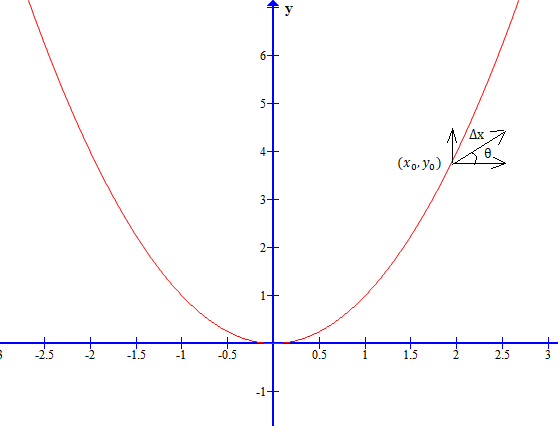
还是老规矩,先从二维平面场景开始,由易到难,步步深入,先上图:
为了方便思考,我们求解的是对上述函数图像的任意一个点![]() 来说,沿着哪个方向走能够使得该函数的y上升幅度最大,那么逆向思维,该方向一旦求得,该方向的反方向不就是使得y下降速度最快的方向了吗?好,沿着这个思路继续,由于这个方向是我们要求的,不妨设该方向与x轴的夹角为
来说,沿着哪个方向走能够使得该函数的y上升幅度最大,那么逆向思维,该方向一旦求得,该方向的反方向不就是使得y下降速度最快的方向了吗?好,沿着这个思路继续,由于这个方向是我们要求的,不妨设该方向与x轴的夹角为![]() ,现在我们沿着这个方向走
,现在我们沿着这个方向走![]() 的距离,将该向量正交分解可知,它只有在水平方向上的分量才会提供使得函数值发生变化的效果,竖直方向上分量不产生任何效果,于是可得以下函数值变化量函数:
的距离,将该向量正交分解可知,它只有在水平方向上的分量才会提供使得函数值发生变化的效果,竖直方向上分量不产生任何效果,于是可得以下函数值变化量函数:
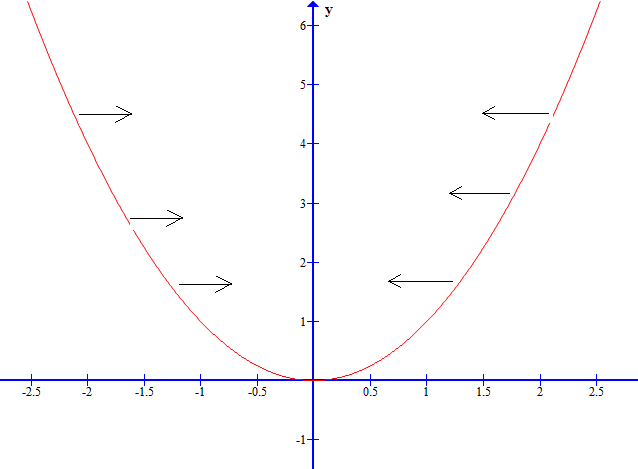
显然,当 ![]() 为0,也就是水平正方向时,可使得该函数值上升最快,也就是说水平负方向可使得该函数值下降最快,至此,二维平面上的使得函数值下降最快的方向我们就找到了:
为0,也就是水平正方向时,可使得该函数值上升最快,也就是说水平负方向可使得该函数值下降最快,至此,二维平面上的使得函数值下降最快的方向我们就找到了:
2. 原理讲解——三维空间情形
现将该问题拓展至三维空间上,由之前的证明可知,对于函数![]() 来说,某向量在y轴上的分量不会提供使得函数值发生变化的效果,那么将此结论扩展,对于函数
来说,某向量在y轴上的分量不会提供使得函数值发生变化的效果,那么将此结论扩展,对于函数![]() 来说,某向量在z轴上的分量也不会提供使得函数值发生变化的效果,因此,我们可以这样说,该问题的最终解必落在xoy平面内,而与z轴无关!现正式开始证明
来说,某向量在z轴上的分量也不会提供使得函数值发生变化的效果,因此,我们可以这样说,该问题的最终解必落在xoy平面内,而与z轴无关!现正式开始证明
设![]() 为xoy平面上的一个向量,该向量与x轴的夹角为
为xoy平面上的一个向量,该向量与x轴的夹角为![]() ,则它在x轴和y轴上的分量为:
,则它在x轴和y轴上的分量为:
x轴和y轴的变化共同引起了z轴方向上的变化,由此可得:
利用向量的思想,将上式表示成两个向量内积的结果,可得:
第一个向量其实就是向量![]() ,而第二个向量就是函数
,而第二个向量就是函数![]() 在某点上的梯度
在某点上的梯度![]() ,因此上式最终就可转换成:
,因此上式最终就可转换成:
![]()
设上式中两个向量的夹角为α,根据向量内积公式,又可表示成:
![]()
该式中,当α为0时达到最大值,也就是说,与梯度相同的方向是使得函数值上升最快的方向,换句话来说,与梯度相反的方向是使得函数值下降最快的方向!!!
3. 原理讲解——高维空间情形
结合上一篇博客中提到的高维空间下的SSE的计算,我们直接引用之前的结论:
若采用梯度下降法求解最小值,只需沿着上式的方向进行试探即可
4. 代码实现
目前常见的求解梯度下降法的方式有三种,BGD,Batch Gradient Descent,批量梯度下降法,SGD,Stochastic Gradient Descent,随机梯度下降法,以及MBGD,Mini-Batch Gradient Descent,小批量梯度下降法。由于最为普通的批量梯度下降法是每次迭代都是对于全量的数据来说的,若初值选的不巧就比较容易陷入一个局部(local)最优而不是全局(global)最优的解中去,因此出现了一个更为优化的算法来解决这个问题,那就是随机梯度下降法,在SGD中,每个循环只随机选取一个样本进行迭代,因此对于BGD来说,训练模型的速度明显快上了许多,但由于每次仅仅选用一个样本,样本量不够,因此不能够很快收敛到最优解,值得一提的是,由于该算法的随机性,在面对非凸函数时,能很好地避免陷入局部最优的情况,因此比BGD效果更好;然后这两种算法都比较极端,要么每次选择全部,要么每次只选一个,有没有一种折中的算法呢?答案是肯定的,那就是MBGD,小批量梯度下降法,每次选择的样本量是在总体中进行一次抽样,一般以比例的方式抽取最佳。
4.1 关于步长大小的选择
虽说在实际写代码的时候,步长是我们自己设定的,但对于步长究竟选择多少合适,主要有两点考量。
1. 步长过小会导致一步步迭代到最优值的过程会非常长,不过结果会较为精确,需要注意的是,倘若迭代次数不够,就会导致最终结果往往不是最优解
2. 步长过长虽然可以使得迭代过程缩短,但是对于精度丢失会比较大,并且最终解很有可能会在最有点两侧来回跳动,导致始终接近不了最优解
4.2 三种算法代码实现
我们使用python将这三种算法写进一个包中,功能是使用梯度下降法来纠结回归方程SSE的最小值,具体代码如下所示:
import numpy as np import pandas as pd class regression: def __init__(self, data, intercept = True): self.X = np.mat(data.iloc[:,:-1].values) self.Y = np.mat(data.iloc[:,-1].values).T self.data = data self.intercept = intercept def BGDfit(self, lam, iternum): #This function aims to use batch gradient descent algorithm to get the minimum value theta = np.mat(np.zeros((self.X.shape[1], 1))) for _ in range(iternum): grad = 2 / self.X.shape[0] * (self.X.T * (self.X * theta - self.Y)) theta -= lam * grad return np.ravel(theta) def SGDfit(self, lam, iternum): #This function aims to use stochastic gradient descent algorithm to get the minimum value theta = np.mat(np.zeros((self.X.shape[1], 1))) for _ in range(iternum): rnd_num = np.random.randint(self.X.shape[0]) grad = 2 / self.X.shape[0] * (self.X[rnd_num].T * (self.X[rnd_num] * theta - self.Y[rnd_num])) theta -= lam * grad return np.ravel(theta) def MBGDfit(self, lam, iternum): #This function aims to use mini-batch gradient descent algorithm to get the minimum value theta = np.mat(np.zeros((self.X.shape[1], 1))) temp_X = pd.DataFrame(self.X) for _ in range(iternum): X_index = temp_X.sample(frac = 0.1, replace = False).index X_mini = self.X[X_index, :] Y_mini = self.Y[X_index] grad = 2 / X_mini.shape[0] * (X_mini.T * (X_mini * theta - Y_mini)) theta -= lam * grad return np.ravel(theta) def evaluate(self, coef): #This function aims to calculate SSE and R2 in order to evaluate whether the model is accurate or not Y_pred = self.X * np.mat(coef).T SSE = np.power(np.ravel(self.Y) - np.ravel(Y_pred), 2).sum() SST = np.power(np.ravel(self.Y) - np.ravel(self.Y).mean(), 2).sum() R2 = 1 - SSE / SST return SSE, R2