本文首发于我的博客 https://huanghaozi.cn, 原链接本篇文章由一文多发平台ArtiPub自动发布
本文将由一个神经网络应用实例——用程序玩扫雷 引入,从大家较为熟悉的回归入手,介绍部分神经网络的原理。需要注意的是,由于作者很菜,本文可能有很多问题,如有大佬发现,请在评论中指正,感谢!
做一个机器人打游戏的抽象思路
举一个很简单的例子,扫雷
(Win10莫有灵魂的扫雷)
扫雷的基本玩法,就是通过一个格子周围的数字判断这个格子是否有雷,一开始一般是乱点,点出来一片之后就可以通过逻(xia)辑(cai)来判断周围格子是否有雷
这个游戏看起来很复杂,但是,我们可以把它抽象一下,玩游戏的过程,大概就是一个输入,处理,输出的过程
其中,
输入的东西是:每一个坐标格与其对应的数、还剩几个雷
输出的东西是:每一个坐标格 没有雷的概率 (选取最高的摁下去)
所以问题就简单啦!我们只要生成一下中间的处理过程就能做出来个自动扫雷机器人啦!那问题也就lei了,这个中间过程该zha办嘞?
我们可以对这个游戏过程进行逻辑上的分析。但是,如果换个游戏,又该zha办嘞?
所以想一想,有什么数学过程,是可以在知道很多组输入、输出时,自动生成中间模型的嘞?
答案就是 回归
从回归讲起
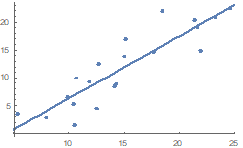
仔细回忆一下,什么是回归?大概就是下面这个图的亚子:
上图中,输入是X,输出是Y,中间的过程是那条线
回归的过程,大概就是从一堆散点拟合出来一条线来
那么拟合的过程是什么嘞?——最小二乘法
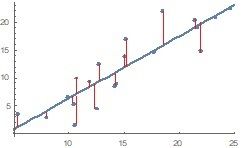
最小二乘法,简单的说,就是使图里的散点Y值到拟合线Y值距离的平方和最小。这个距离如下图所示:
具体的计算过程就是下面这样的:
上面的拟合线是一条直线,也可以将其换成任意的函数形式,具体需要看散点像什么函数
但是,现实往往就很残酷,比如我们上面说的自动扫雷机器人模型,它的输入和输出,不是一个数,是一组数,而且,它的函数关系很复杂,肯定不是一条直线那么简单,而且也没办法通过看它像什么函数来判断它的函数形式。
而神经网络就可以很好地解决这个问题!
神经网络又是什么?
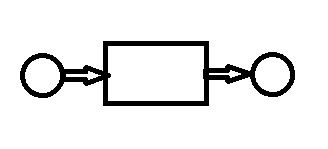
最简单的那个神经网络模型和回归很像,是下面这个图这样:
也是一个输入,一个输出,不过中间是一团乱糟糟的东西
把这个模型想成一个函数,输入一堆数,经过中间的运算,输出一堆数,那中间那团乱糟糟的运算具体是怎么算的嘞?
其实在神经网络里,每一个圈圈都是一个神经元,箭头就是它的输入输出,它是有具体形式的:
里面有k1、k2、k3、b...是不是很熟悉?其实就是线性回归那条直线的形式,不过还得加一层激活函数A()才行,不然模型训练出来真就和线性回归一样出来条直线啦
(其中的k1、k2、k3一般叫权重,用w表示)
(训练和回归里的拟合是差不多的意思,都是在两头加一堆数据(散点)生成中间的模型)
激活函数有很多种,选择很玄学,本文只是粗略讲解,所以不深究
这样的一个个神经元组成一个最简单的网络,就是从输入数据开始一层一层地往前输出,每一层就可以看作一组数据往前跑
(这样一个复杂的网络,手算基本8可能哒,乖乖用计算机叭)
那么,该如何训练模型得出里面的k1、k2、k3、b这些权重嘞?和回归很像,有一个叫反向传播的算法
反向传播
回忆一下回归里求k和b的算法,核心就是令离差(拟合值与真实值的差距)最小
对应的,神经网络的每一个神经元都可以看作一个回归方程(不过套了一个激活函数),我们回忆一下回归里的离差平方和(令它最小)
$y_{拟合线}$其实就是神经网络最后一层的输出,最后一层和它上一层其实就是一组套了激活函数的回归方程,把这组方程代入那个离差平方和,用梯度下降(其实也是导数)算它最小值
然后我们会发现这个式子里并没有倒数第二层的输出值,而倒数第二层又是和前一层的回归,对应我们需要把倒数第二层代进去....(这就是反向传播了)
不过....这样还没法算,因为必须代,代,代,最后代到x才能回归,而且还存在激活函数....就很难一次性算出
有一个解决办法,就是先设定一个初始权重,输入一组数据,得到一组输出,再输入一组数据,再得到一组输出,得到N组输入输出,再进行反向传播,这样就能进行计算了
既然有设定初始权重,那输入一组数据,就能得到每个神经元的输出啦,所以从最后一层开始,根据最后一层每个神经元与倒数第二层之间的回归关系式,以及N组输出结果与实际结果的差异,令其最小,就可以更新上一层的权重
这样一步一步往前更新权重,就得到中间的模型啦!
本篇文章由一文多发平台ArtiPub自动发布