卡特兰数的证明及其应用

卡特兰数又称卡塔兰数，卡特兰数是组合数学中一个常出现在各种记数问题中的数列。

原理：

设h(n)为catalan数的第n+1项，令h(0)=1,h(1)=1，catalan数满足递推式  ：

h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)

 

例如：h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2

h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5

 

另类递推式：

h(n)=h(n-1)*(4*n-2)/(n+1);

 

递推关系的解为：

h(n)=C(2n,n)/(n+1) (n=0,1,2,...)

 

递推关系的另类解为：（ c(2n,n-1)与c(2n,n+1)是一样的，排列组合知识 ）

h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...)

 

 

下面通过一个例题来体现其递推式的产生过程

一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?（进栈的顺序已经确定了，且n>=2）

1.我们设  f（n）=序列个数为n的出栈序列种数。同时，我们假定，从开始到栈第一次出到空为止，这段过程中第一个出栈的序数是k。特别地，如果栈直到整个过程结束时才空，则k=n。

2.第一个出栈的序数k将1~n的序列分成两个序列，其中一个序列是1~k-1，序列个数为k-1，另外一个序列是k+1~n，序列个数是n-k。

3.我们若把k视为确定一个序数，那么根据乘法原理，f（n）的问题就等价于——序列个数为k-1的出栈序列种数乘以序列个数为n - k的出栈序列种数，即选择k这个序数的 f（n）=f（k-1）×f（n-k）。而k可以选1到n，所以再根据加法原理，将k取不同值的序列种数相加，得到的总序列种数为：f（n）=f（0）f（n-1）+f（1）f（n-2）+……+f（n-1）f（0）。（ f (0)==1 f(1)==1)，所以此问题的求解式满足卡特兰数的原理的。

4.卡特兰数的递推关系的解，即求出此问题不同出栈顺序有多少。我们用折现法来证明。

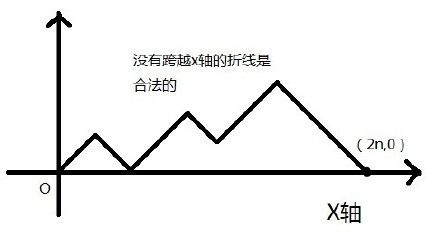
事实上，可以认为问题是，任意两种操作（入栈和出栈），要求每种操作的总次数一样，且进行第k次出栈前必须先进行至少k次入栈。我们假设一个人在原点，入栈是此人沿右上角45°走一个单位（一个单位设为根号2，这样他第一次进行操作1就刚好走到（1,1）点），出栈是此人沿右下角45°走一个单位。第k次出栈前必须先进行至少k次入栈，就是说明所走出来的折线不能跨越x轴走到y=-1这条线上！在进行n次入栈和n次出栈后，此人必将到到达（2n，0）！若无跨越x轴的限制，折线的种数将为 C（2n，n），即在2n次操作中选出n次作为入栈的方法数。

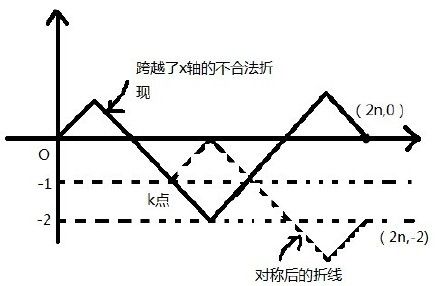
现在只要减去跨越了x轴的情况数。对于任意跨越x轴的折线情况，必有将与y=-1相交的点。找出第一个与y=-1相交的点k，将k点以右的折线根据y=-1对称（即后面曲线的变化规律是反的但是数量上是保持一致的）。可以发现终点最终都会从（2n，0）对称到（2n，-2）（因为的坐标终点是固定的）。由于对称总是能进行的，且是可逆的。（即所求不同折线的总数是一样的，等价的）我们可以得出所有跨越了x轴的折线总数是与从（0,0）到（2n,-2）的折线总数数量相等。撇开k点后的实线折线图不管，虚线表示的其实就是入栈和出栈的总数是2n，而出栈的数量比入栈多了一次（不必在意其在文字上的合理性，我们只是需要求出其值）那么出栈就出了n+1次，入栈就入了n-1次。所以其不同折线数量为C（2n,n-1) or C (2n,n+1).

所以卡特兰数递推关系的解为f(n)=C(2n,n)-C(2n,n-1) or f(n)=C(2n,n)-C(2n,n+1)。