启发式搜索A*算法
概述
虽然掌握了 A* 算法的人认为它容易,但是对于初学者来说, A* 算法还是很复杂的。
搜索区域(The Search Area)
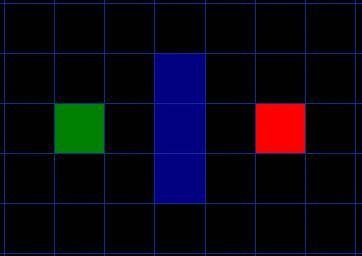
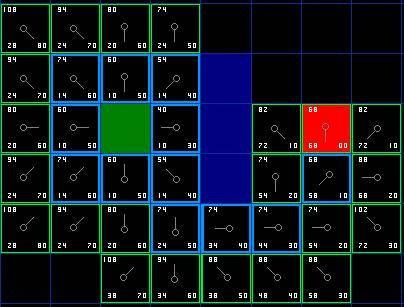
我们假设某人要从 A 点移动到 B 点,但是这两点之间被一堵墙隔开。如图 1 ,绿色是 A ,红色是 B ,中间蓝色是墙。
图 1
你应该注意到了,我们把要搜寻的区域划分成了正方形的格子。这是寻路的第一步,简化搜索区域,就像我们这里做的一样。这个特殊的方法把我们的搜索区域简化为了 2 维数组。数组的每一项代表一个格子,它的状态就是可走 (walkalbe) 和不可走 (unwalkable) 。通过计算出从 A 到 B 需要走过哪些方格,就找到了路径。一旦路径找到了,人物便从一个方格的中心移动到另一个方格的中心,直至到达目的地。
方格的中心点我们成为“节点 (nodes) ”。如果你读过其他关于 A* 寻路算法的文章,你会发现人们常常都在讨论节点。为什么不直接描述为方格呢?因为我们有可能把搜索区域划为为其他多变形而不是正方形,例如可以是六边形,矩形,甚至可以是任意多变形。而节点可以放在任意多边形里面,可以放在多变形的中心,也可以放在多边形的边上。我们使用这个系统,因为它最简单。
开始搜索(Starting the Search)
一旦我们把搜寻区域简化为一组可以量化的节点后,就像上面做的一样,我们下一步要做的便是查找最短路径。在 A* 中,我们从起点开始,检查其相邻的方格,然后向四周扩展,直至找到目标。
我们这样开始我们的寻路旅途:
1. 从起点 A 开始,并把它就加入到一个由方格组成的 open list( 开放列表 ) 中。这个 open list 有点像是一个购物单。当然现在 open list 里只有一项,它就是起点 A ,后面会慢慢加入更多的项。 Open list 里的格子是路径可能会是沿途经过的,也有可能不经过。基本上 open list 是一个待检查的方格列表。
2. 查看与起点 A 相邻的方格 ( 忽略其中墙壁所占领的方格,河流所占领的方格及其他非法地形占领的方格 ) ,把其中可走的 (walkable) 或可到达的 (reachable) 方格也加入到 open list 中。把起点 A 设置为这些方格的父亲 (parent node 或 parent square) 。当我们在追踪路径时,这些父节点的内容是很重要的。稍后解释。
3. 把 A 从 open list 中移除,加入到 close list( 封闭列表 ) 中, close list 中的每个方格都是现在不需要再关注的。
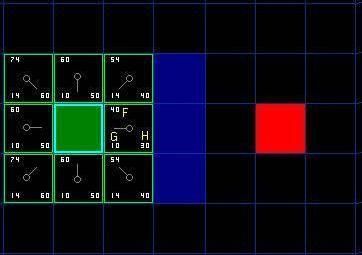
如下图所示,深绿色的方格为起点,它的外框是亮蓝色,表示该方格被加入到了 close list 。与它相邻的黑色方格是需要被检查的,他们的外框是亮绿色。每个黑方格都有一个灰色的指针指向他们的父节点,这里是起点 A 。
图 2 。
下一步,我们需要从 open list 中选一个与起点 A 相邻的方格,按下面描述的一样或多或少的重复前面的步骤。但是到底选择哪个方格好呢?具有最小 F 值的那个。
路径排序(Path Sorting)
计算出组成路径的方格的关键是下面这个等式:
F = G + H
这里,
G = 从起点 A 移动到指定方格的移动代价,沿着到达该方格而生成的路径。
H = 从指定的方格移动到终点 B 的估算成本。这个通常被称为试探法,有点让人混淆。为什么这么叫呢,因为这是个猜测。直到我们找到了路径我们才会知道真正的距离,因为途中有各种各样的东西 ( 比如墙壁,水等 ) 。本教程将教你一种计算 H 的方法,你也可以在网上找到其他方法。
我们的路径是这么产生的:反复遍历 open list ,选择 F 值最小的方格。这个过程稍后详细描述。我们还是先看看怎么去计算上面的等式。
如上所述, G 是从起点A移动到指定方格的移动代价。在本例中,横向和纵向的移动代价为 10 ,对角线的移动代价为 14 。之所以使用这些数据,是因为实际的对角移动距离是 2 的平方根,或者是近似的 1.414 倍的横向或纵向移动代价。使用 10 和 14 就是为了简单起见。比例是对的,我们避免了开放和小数的计算。这并不是我们没有这个能力或是不喜欢数学。使用这些数字也可以使计算机更快。稍后你便会发现,如果不使用这些技巧,寻路算法将很慢。
既然我们是沿着到达指定方格的路径来计算 G 值,那么计算出该方格的 G 值的方法就是找出其父亲的 G 值,然后按父亲是直线方向还是斜线方向加上 10 或 14 。随着我们离开起点而得到更多的方格,这个方法会变得更加明朗。
有很多方法可以估算 H 值。这里我们使用 Manhattan 方法,计算从当前方格横向或纵向移动到达目标所经过的方格数,忽略对角移动,然后把总数乘以 10 。之所以叫做 Manhattan 方法,是因为这很像统计从一个地点到另一个地点所穿过的街区数,而你不能斜向穿过街区。重要的是,计算 H 是,要忽略路径中的障碍物。这是对剩余距离的估算值,而不是实际值,因此才称为试探法。
把 G 和 H 相加便得到 F 。我们第一步的结果如下图所示。每个方格都标上了 F , G , H 的值,就像起点右边的方格那样,左上角是 F ,左下角是 G ,右下角是 H 。
图 3
好,现在让我们看看其中的一些方格。在标有字母的方格, G = 10 。这是因为水平方向从起点到那里只有一个方格的距离。与起点直接相邻的上方,下方,左方的方格的 G 值都是 10 ,对角线的方格 G 值都是 14 。
H 值通过估算起点于终点 ( 红色方格 ) 的 Manhattan 距离得到,仅作横向和纵向移动,并且忽略沿途的墙壁。使用这种方式,起点右边的方格到终点有 3 个方格的距离,因此 H = 30 。这个方格上方的方格到终点有 4 个方格的距离 ( 注意只计算横向和纵向距离 ) ,因此 H = 40 。对于其他的方格,你可以用同样的方法知道 H 值是如何得来的。
每个方格的 F 值,再说一次,直接把 G 值和 H 值相加就可以了。
继续搜索(Continuing the Search)
为了继续搜索,我们从 open list 中选择 F 值最小的 ( 方格 ) 节点,然后对所选择的方格作如下操作:
4. 把它从 open list 里取出,放到 close list 中。
5. 检查所有与它相邻的方格,忽略其中在 close list 中或是不可走 (unwalkable) 的方格 ( 比如墙,水,或是其他非法地形 ) ,如果方格不在 open lsit 中,则把它们加入到 open list 中。
把我们选定的方格设置为这些新加入的方格的父亲。
6. 如果某个相邻的方格已经在 open list 中,则检查这条路径是否更优,也就是说经由当前方格 ( 我们选中的方格 ) 到达那个方格是否具有更小的 G 值。如果没有,不做任何操作。
相反,如果 G 值更小,则把那个方格的父亲设为当前方格 ( 我们选中的方格 ) ,然后重新计算那个方格的 F 值和 G 值。如果你还是很混淆,请参考下图。
图 4
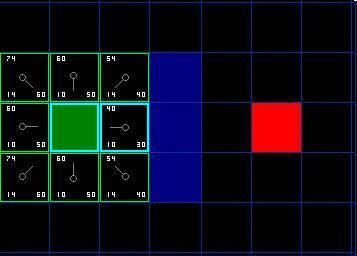
Ok ,让我们看看它是怎么工作的。在我们最初的 9 个方格中,还有 8 个在 open list 中,起点被放入了 close list 中。在这些方格中,起点右边的格子的 F 值 40 最小,因此我们选择这个方格作为下一个要处理的方格。它的外框用蓝线打亮。
首先,我们把它从 open list 移到 close list 中 ( 这就是为什么用蓝线打亮的原因了 ) 。然后我们检查与它相邻的方格。它右边的方格是墙壁,我们忽略。它左边的方格是起点,在 close list 中,我们也忽略。其他 4 个相邻的方格均在 open list 中,我们需要检查经由这个方格到达那里的路径是否更好,使用 G 值来判定。让我们看看上面的方格。它现在的 G 值为 14 。如果我们经由当前方格到达那里, G 值将会为 20( 其中 10 为到达当前方格的 G 值,此外还要加上从当前方格纵向移动到上面方格的 G 值 10) 。显然 20 比 14 大,因此这不是最优的路径。如果你看图你就会明白。直接从起点沿对角线移动到那个方格比先横向移动再纵向移动要好。
当把 4 个已经在 open list 中的相邻方格都检查后,没有发现经由当前方格的更好路径,因此我们不做任何改变。现在我们已经检查了当前方格的所有相邻的方格,并也对他们作了处理,是时候选择下一个待处理的方格了。
因此再次遍历我们的 open list ,现在它只有 7 个方格了,我们需要选择 F 值最小的那个。有趣的是,这次有两个方格的 F 值都 54 ,选哪个呢?没什么关系。从速度上考虑,选择最后加入 open list 的方格更快。这导致了在寻路过程中,当靠近目标时,优先使用新找到的方格的偏好。但是这并不重要。 ( 对相同数据的不同对待,导致两中版本的 A* 找到等长的不同路径 ) 。
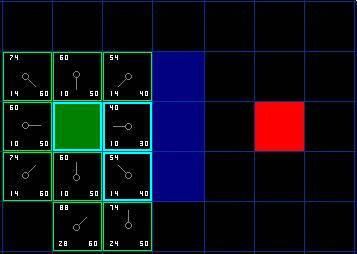
我们选择起点右下方的方格,如下图所示。
图 5
这次,当我们检查相邻的方格时,我们发现它右边的方格是墙,忽略之。上面的也一样。
我们把墙下面的一格也忽略掉。为什么?因为如果不穿越墙角的话,你不能直接从当前方格移动到那个方格。你需要先往下走,然后再移动到那个方格,这样来绕过墙角。 ( 注意:穿越墙角的规则是可选的,依赖于你的节点是怎么放置的 )
这样还剩下 5 个相邻的方格。当前方格下面的 2 个方格还没有加入 open list ,所以把它们加入,同时把当前方格设为他们的父亲。在剩下的 3 个方格中,有 2 个已经在 close list 中 ( 一个是起点,一个是当前方格上面的方格,外框被加亮的 ) ,我们忽略它们。最后一个方格,也就是当前方格左边的方格,我们检查经由当前方格到达那里是否具有更小的 G 值。没有。因此我们准备从 open list 中选择下一个待处理的方格。
不断重复这个过程,直到把终点也加入到了 open list 中,此时如下图所示。
图 6
注意,在起点下面 2 格的方格的父亲已经与前面不同了。之前它的 G 值是 28 并且指向它右上方的方格。现在它的 G 值为 20 ,并且指向它正上方的方格。这在寻路过程中的某处发生,使用新路径时 G 值经过检查并且变得更低,因此父节点被重新设置, G 和 F 值被重新计算。尽管这一变化在本例中并不重要,但是在很多场合中,这种变化会导致寻路结果的巨大变化。
那么我们怎么样去确定实际路径呢?很简单,从终点开始,按着箭头向父节点移动,这样你就被带回到了起点,这就是你的路径。如下图所示。从起点 A 移动到终点 B 就是简单从路径上的一个方格的中心移动到另一个方格的中心,直至目标。就是这么简单!
图 7
A*算法总结(Summary of the A* Method)
Ok ,现在你已经看完了整个的介绍,现在我们把所有步骤放在一起:
1. 把起点加入 open list 。
2. 重复如下过程:
a. 遍历 open list ,查找 F 值最小的节点,把它作为当前要处理的节点。
b. 把这个节点移到 close list 。
c. 对当前方格的 8 个相邻方格的每一个方格?
◆ 如果它是不可抵达的或者它在 close list 中,忽略它。否则,做如下操作。
◆ 如果它不在 open list 中,把它加入 open list ,并且把当前方格设置为它的父亲,记录该方格的 F , G 和 H 值。
◆ 如果它已经在 open list 中,检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好,用 G 值作参考。更小的 G 值表示这是更好的路径。如果是这样,把它的父亲设置为当前方格,并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话,改变后你可能需要重新排序。
d. 停止,当你
◆ 把终点加入到了 open list 中,此时路径已经找到了,或者
◆ 查找终点失败,并且 open list 是空的,此时没有路径。
3. 保存路径。从终点开始,每个方格沿着父节点移动直至起点,这就是你的路径。
启发式搜索A*算法
据 Drew 所知最短路经算法现在重要的应用有计算机网络路由算法,机器人探路,交通路线导航,人工智能,游戏设计等等。美国火星探测器核心的寻路算法就是采用的D*(D Star)算法。
最短路经计算分静态最短路计算和动态最短路计算。
静态路径最短路径算法是外界环境不变,计算最短路径。主要有Dijkstra算法,A*(A Star)算法。
动态路径最短路是外界环境不断发生变化,即不能计算预测的情况下计算最短路。如在游戏中敌人或障碍物不断移动的情况下。典型的有D*算法。
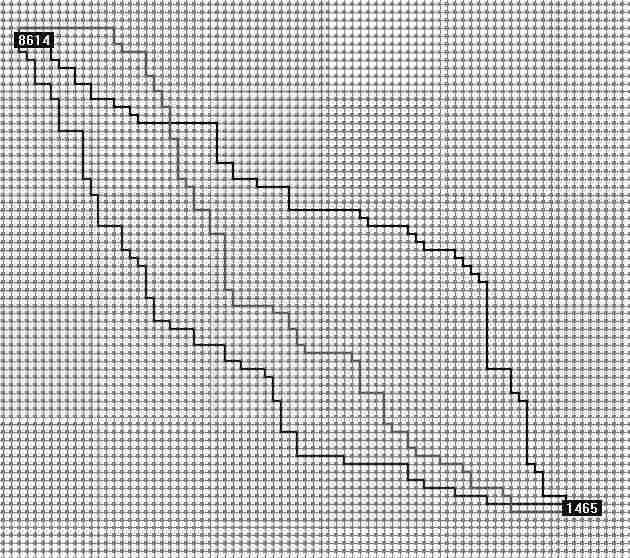
这是Drew程序实现的10000个节点的随机路网三条互不相交最短路
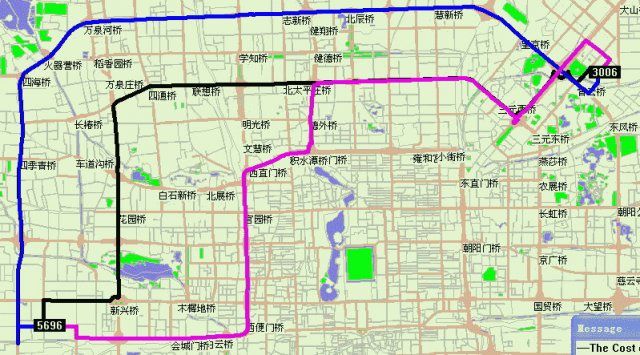
真实路网计算K条路径示例:节点5696到节点3006,三条最快速路,可以看出路径基本上走环线或主干路。黑线为第一条,兰线为第二条,红线为第三条。约束条件系数为1.2。共享部分路段。显示计算部分完全由Drew自己开发的程序完成。
参见 K条路算法测试程序
Dijkstra算法求最短路径:
Dijkstra算法是典型最短路算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
Dijkstra算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
Dijkstra一般的表述通常有两种方式,一种用永久和临时标号方式,一种是用OPEN, CLOSE表方式,Drew为了和下面要介绍的 A* 算法和 D* 算法表述一致,这里均采用OPEN,CLOSE表的方式。
大概过程:
创建两个表,OPEN, CLOSE。
OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。
1. 访问路网中里起始点最近且没有被检查过的点,把这个点放入OPEN组中等待检查。
2. 从OPEN表中找出距起始点最近的点,找出这个点的所有子节点,把这个点放到CLOSE表中。
3. 遍历考察这个点的子节点。求出这些子节点距起始点的距离值,放子节点到OPEN表中。
4. 重复2,3,步。直到OPEN表为空,或找到目标点。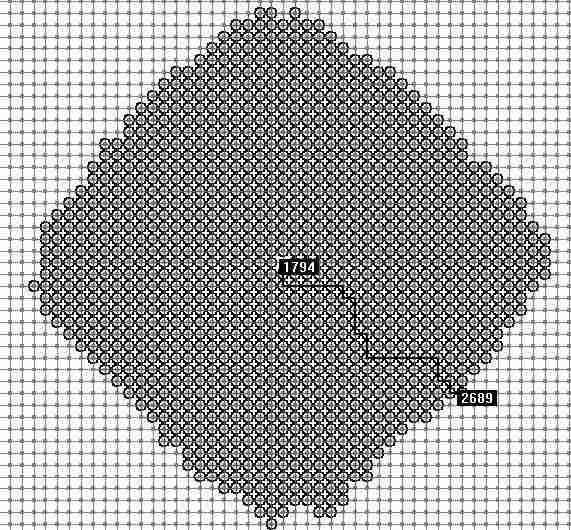
这是在drew 程序中4000个节点的随机路网上Dijkstra算法搜索最短路的演示,黑色圆圈表示经过遍历计算过的点由图中可以看到Dijkstra算法从起始点开始向周围层层计算扩展,在计算大量节点后,到达目标点。所以速度慢效率低。
提高Dijkstra搜索速度的方法很多,据Drew所知,常用的有数据结构采用Binary heap的方法,和用Dijkstra从起始点和终点同时搜索的方法。
推荐网页:http://www.cs.ecnu.edu.cn/assist/js04/ZJS045/ZJS04505/zjs045050a.htm
简明扼要介绍Dijkstra算法,有图解显示和源码下载。
A*(A Star)算法:启发式(heuristic)算法
A*(A-Star)算法是一种静态路网中求解最短路最有效的方法。
公式表示为: f(n)=g(n)+h(n),
其中f(n) 是节点n从初始点到目标点的估价函数,
g(n) 是在状态空间中从初始节点到n节点的实际代价,
h(n)是从n到目标节点最佳路径的估计代价。保证找到最短路径(最优解的)条件,关键在于估价函数h(n)的选取:
估价值h(n)<= n到目标节点的距离实际值,这种情况下,搜索的点数多,搜索范围大,效率低。但能得到最优解。
如果 估价值>实际值, 搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
估价值与实际值越接近,估价函数取得就越好。
例如对于几何路网来说,可以取两节点间欧几理德距离(直线距离)做为估价值,即f=g(n)+sqrt((dx-nx)*(dx-nx)+(dy-ny)*(dy-ny));这样估价函数f在g值一定的情况下,会或多或少的受估价值h的制约,节点距目标点近,h值小,f值相对就小,能保证最短路的搜索向终点的方向进行。明显优于Dijstra算法的毫无无方向的向四周搜索。
conditions of heuristic
Optimistic (must be less than or equal to the real cost)
As close to the real cost as possible
主要搜索过程:
创建两个表,OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。
遍历当前节点的各个节点,将n节点放入CLOSE中,取n节点的子节点X,->算X的估价值->
While(OPEN!=NULL)
{
从OPEN表中取估价值f最小的节点n;
if(n节点==目标节点) break;
else
{
if(X in OPEN) 比较两个X的估价值f //注意是同一个节点的两个不同路径的估价值
if( X的估价值小于OPEN表的估价值 )
更新OPEN表中的估价值; //取最小路径的估价值
if(X in CLOSE) 比较两个X的估价值 //注意是同一个节点的两个不同路径的估价值
if( X的估价值小于CLOSE表的估价值 )
更新CLOSE表中的估价值; 把X节点放入OPEN //取最小路径的估价值
if(X not in both)
求X的估价值;
并将X插入OPEN表中; //还没有排序
}
将n节点插入CLOSE表中;
按照估价值将OPEN表中的节点排序; //实际上是比较OPEN表内节点f的大小,从最小路径的节点向下进行。
}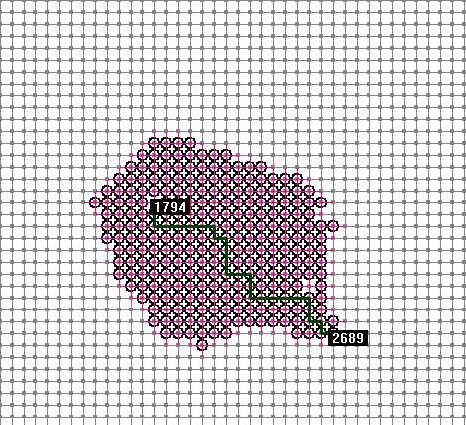
上图是和上面Dijkstra算法使用同一个路网,相同的起点终点,用A*算法的情况,计算的点数从起始点逐渐向目标点方向扩展,计算的节点数量明显比Dijkstra少得多,效率很高,且能得到最优解。
A*算法和Dijistra算法的区别在于有无估价值,Dijistra算法相当于A*算法中估价值为0的情况。
推荐文章链接:
Amit 斯坦福大学一个博士的游戏网站,上面有关于A*算法介绍和不少有价值的链接 http://theory.stanford.edu/~amitp/GameProgramming/
Sunway写的两篇很好的介绍启发式和A*算法的中文文章并有A*源码下载:
初识A*算法 http://creativesoft.home.shangdu.net/AStart1.htm
深入A*算法 http://creativesoft.home.shangdu.net/AStart2.htm
需要注意的是Sunway上面文章“深入A*算法”中引用了一个A*的游戏程序进行讲解,并有这个源码的下载,不过它有一个不小的Bug, 就是新的子节点放入OPEN表中进行了排序,而当子节点在Open表和Closed表中时,重新计算估价值后,没有重新的对Open表中的节点排序,这个问题会导致计算有时得不到最优解,另外在路网权重悬殊很大时,搜索范围不但超过Dijkstra,甚至搜索全部路网, 使效率大大降低。
Drew 对这个问题进行了如下修正,当子节点在Open表和Closed表中时,重新计算估价值后,删除OPEN表中的老的节点,将有新估价值的节点插入OPEN表中,重新排序,经测试效果良好,修改的代码如下,红色部分为Drew添加的代码.添加进程序的相应部分即可。
在函数GenerateSucc()中
...................................
g=BestNode->g+1;
TileNumS=TileNum((int)x,(int)y);
if ((Old=CheckOPEN(TileNumS)) != NULL)
{
for(c=0;c<8;c++)
if(BestNode->Child[c] == NULL)
break;
BestNode->Child[c]=Old;
if (g < Old->g)
{
Old->Parent=BestNode;
Old->g=g;
Old->f=g+Old->h;
//Drew 在该处添加如下红色代码
//Implement by Drew
NODE *q,*p=OPEN->NextNode, *temp=OPEN->NextNode;
while(p!=NULL && p->NodeNum != Old->NodeNum)
{
q=p;
p=p->NextNode;
}
if(p->NodeNum == Old->NodeNum)
{
if(p==OPEN->NextNode)
{
temp = temp->NextNode;
OPEN ->NextNode = temp;
}
else
q->NextNode = p->NextNode;
}
Insert(Old); // Insert Successor on OPEN list wrt f
}
......................................................
另一种A*(A Star)算法:
这种算法可以不直接用估价值,直接用Dijkstra算法程序实现A*算法,Drew对它进行了测试,达到和A*完全一样的计算效果,且非常简单。
以邻接矩阵为例,更改原来邻接矩阵i行j列元素Dij为 Dij+Djq-Diq; 起始点到目标点的方向i->j, 终点q. Dij为(i到j路段的权重或距离)
其中:Djq,Diq的作用相当于估价值 Djq=(j到q的直线距离);Diq=(i到q的直线距离)
原理:i 到q方向符合Dij+Djq > Diq ,取Dij+Djq-Diq 小,如果是相反方向Dij+Djq-Diq会很大。因此达到向目标方向寻路的作用。
动态路网,最短路径算法 D*
A* 在静态路网中非常有效(very efficient for static worlds),但不适于在动态路网,环境如权重等不断变化的动态环境下。
D*是动态A*(D-Star,Dynamic A Star)卡内及梅隆机器人中心的Stentz在1994和1995年两篇文章提出,主要用于机器人探路。是火星探测器采用的寻路算法。Optimal and Efficient Path Planning for Partially-Known Environments
The Focussed D* Algorithm for Real-Time Replanning
主要方法(这些完全是Drew在读了上述资料和编制程序中的个人理解,不能保证完全正确,仅供参考):
1.先用Dijstra算法从目标节点G向起始节点搜索。储存路网中目标点到各个节点的最短路和该位置到目标点的实际值h,k(k为所有变化h之中最小的值,当前为k=h。每个节点包含上一节点到目标点的最短路信息1(2),2(5),5(4),4(7)。则1到4的最短路为1-2-5-4。
原OPEN和CLOSE中节点信息保存。
2.机器人沿最短路开始移动,在移动的下一节点没有变化时,无需计算,利用上一步Dijstra计算出的最短路信息从出发点向后追述即可,当在Y点探测到下一节点X状态发生改变,如堵塞。机器人首先调整自己在当前位置Y到目标点G的实际值h(Y),h(Y)=X到Y的新权值c(X,Y)+X的原实际值h(X).X为下一节点(到目标点方向Y->X->G),Y是当前点。k值取h值变化前后的最小。
3.用A*或其它算法计算,这里假设用A*算法,遍历Y的子节点,点放入CLOSE,调整Y的子节点a的h值,h(a)=h(Y)+Y到子节点a的权重C(Y,a),比较a点是否存在于OPEN和CLOSE中,方法如下:
while()
{
从OPEN表中取k值最小的节点Y;
遍历Y的子节点a,计算a的h值 h(a)=h(Y)+Y到子节点a的权重C(Y,a)
{
if(a in OPEN) 比较两个a的h值
if( a的h值小于OPEN表a的h值 )
{
更新OPEN表中a的h值;k值取最小的h值
有未受影响的最短路经存在
break;
}
if(a in CLOSE) 比较两个a的h值 //注意是同一个节点的两个不同路径的估价值
if( a的h值小于CLOSE表的h值 )
{
更新CLOSE表中a的h值; k值取最小的h值;将a节点放入OPEN表
有未受影响的最短路经存在
break;
}
if(a not in both)
将a插入OPEN表中; //还没有排序
}
放Y到CLOSE表;
OPEN表比较k值大小进行排序;
}
机器人利用第一步Dijstra计算出的最短路信息从a点到目标点的最短路经进行。D*算法在动态环境中寻路非常有效,向目标点移动中,只检查最短路径上下一节点或临近节点的变化情况,如机器人寻路等情况。对于距离远的最短路径上发生的变化,则感觉不太适用。
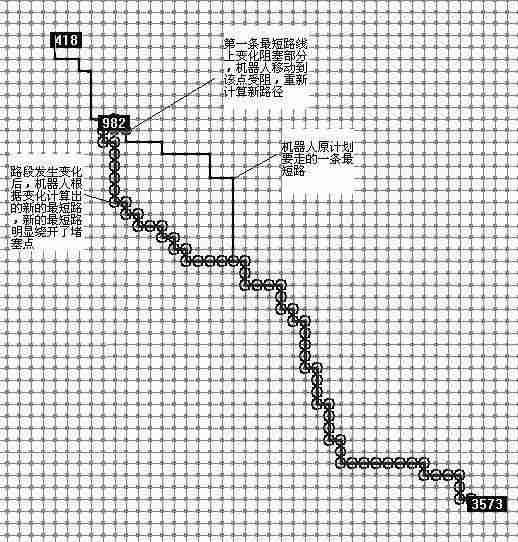
上图是Drew在4000个节点的随机路网上做的分析演示,细黑线为第一次计算出的最短路,红点部分为路径上发生变化的堵塞点,当机器人位于982点时,检测到前面发生路段堵塞,在该点重新根据新的信息计算路径,可以看到圆圈点为重新计算遍历过的点,仅仅计算了很少得点就找到了最短路,说明计算非常有效,迅速。绿线为计算出的绕开堵塞部分的新的最短路径。