地图投影简明笔记
原文见我的博客主站,,欢迎大家过去评论。
地图投影,是将地球表面投影到地图平面的过程,将地理坐标转换为平面直角坐标的过程。因为毕业论文需要,我重新回顾了一下地图投影的知识并且作了比较全面且简洁的总结。如果你之前未系统了解过地图投影,又对地图投影感兴趣,这篇博文也许能成为一篇简洁务实的阅读材料。
还有,这篇文章就不考虑大地基准面了,直接把地球当做一个完美的球体来看待。还有,本篇只介绍最基本的三种投影,方位、圆柱、圆锥投影,更多的投影基本是在这三种投影的基础上派生出来的,在了解这三种投影的基础上,去学习和实现其他的派生投影,会比较轻松。
首先看三种最基本的投影系列,方位投影、圆柱投影和圆锥投影。每种投影都按照等面积,等距离,等角和正轴,横轴,斜轴或者其他的性质分成小类。下图显示了方位投影,圆锥投影和圆柱投影的基本样式。
介绍三种投影时,我**只涉及正轴投影**。横轴与斜轴投影转正轴的方法,会在三种投影结束后介绍。
方位投影
方位投影将球面坐标(经度,纬度)投影到极坐标(半径,方向)上,而且满足球面经度等于极坐标中的方向。其最基本的形式为:
$$\begin{matrix}\rho = f(\psi )\ \delta =\lambda \end{matrix}$$
等式左侧的ρ和δ为投影后的极坐标,右侧的φ和λ为纬度和经度,函数f的形式与形变性质有关。
将极坐标转换为直角坐标很简单:
$$\begin{matrix}x=\rho\cos\delta\ y=\rho\sin\delta\end{matrix}$$
另外,还有一些约定,比如R表示地球半径,他基本会出现在投影公式中(不用担心地图和地球一样大,我们还有比例尺)。还有,d(式子)表示微元,还有西经和南纬都用负值表示,这样纬度区间为[-π/2,π/2],经度区间为[-π,π]。
方位投影中的切投影或割投影区别只在一个比例尺,所以都作为切投影来处理。
在确定函数f之前,首先要求算两个参数,就是经线上的长度比m,和纬线上的长度比n。(长度比就是投影后的长度比投影前的长度)。
$$\begin{matrix}m=\frac{d\rho}{R\cdot d(\pi/2-\delta)}\ n=\frac{\rho d\delta}{R\sin(\pi/2-\delta)\cdot d \lambda}\end{matrix}$$
等面积方位投影
等面积的条件是:
$$m\cdot n=1$$
$$\rho d\rho=R^2\sin(\pi/2-\psi)d(\pi/2-\psi)$$
积分:
$$\int\rho d\rho=R^2\int \sin(\pi/2-\psi)d(\pi/2-\psi)$$
得
$$\rho=C-R^2\cos(\pi/2-\psi)$$
C为积分常数,配合边界条件,φ=π/2时ρ=0(如果想投影南极,那就φ=-π/2时ρ=0),求得:
$$\rho=2R\sin\frac{\pi/2-\psi}{2}$$
这就是等面积方位投影的函数f。
等距离方位投影

注意这里等距离只是指经线上等距离。如果想纬线上等距离,那只能显示北半球,南半球的纬线圈肯定比赤道小,但是如果用方位投影,南半球的纬圈在外侧,不可能比赤道小。在北半球,经线上等距离和纬线上等距离不可能同时达到,两者都可以独立地导出互相矛盾的函数f。
等距离的条件是:
$$m=1$$
可导出:
$$\rho=R(\pi/2-\psi)$$
这就是等距离方位投影的函数f。
等角方位投影

等角的条件是:
$$m=n$$
可导出
$$\rho=2R\tan\frac{\pi/2-\psi}{2}$$
这就是等角方位投影的函数f。
一般情况:透视投影
上述只是一些有着特殊性质的方位投影,事实上,在南北极轴上(也就是垂直于投影面的轴)任意取一个点O,利用透视的方法,将球上每一个点P投影到OP与投影面交点上,都是一个方位投影。比如,等角方位投影就是点O在南极点的投影。
点O在无限远时的方位投影,即正射投影,可用来模拟显示三维地球,其公式为:
$$\rho=R\cos(\psi)$$
点O在地球球心时的投影,即球心投影,其公式为:
$$\rho=R\cot(\psi)$$
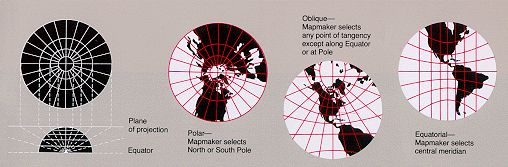
使用极轴上的点O进行投影,并不是方位投影的定义。任何符合条件(f(0)=0且在区间0~x之间单调递增)的函数f,就会有一个方位投影与之对应。
圆柱投影
正轴圆柱投影将球面投影到二维直角坐标上,而且满足投影后经线与y轴平行,纬线与x轴平行。最基本的形式为:
$$\begin{matrix}y = f(\psi )\ x =c\lambda \end{matrix}$$
经线和纬线方向的长度比m和n分别为:
$$\begin{matrix}m=\frac{dy}{Rd\psi}\ n=\frac{dx}{R\cos{\psi}d\lambda}=\frac{c}{Rcos{\psi}}\end{matrix}$$
还是根据等角,等面积和等距离的条件,积分求算不同条件的投影公式。
等角圆柱投影:
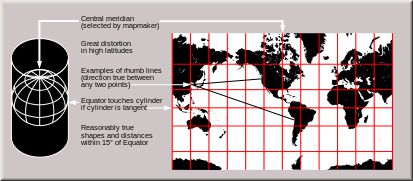
$$y=c\ln \tan(\pi/4+\psi/2)$$
该投影又称墨卡托投影,由于其等角特性,在航海图中应用十分广泛。墨卡托投影也是诸多瓦片式Web地图使用的投影,比如Google地图。该投影无法显示极点附近区域,因为在纬度为-π/2或π/2附近时,y趋向负无穷或正无穷。
等面积圆柱投影:

$$y=R\sin\psi$$
$$c=R$$
等距离圆柱投影(也是指经线上等距离):
$$y=R\psi$$
$$c=R$$
更加一般的表述是,在赤道面上任取一点O,点O将一条经线由球面上,投影到经线所在的子午面与投影圆柱面的交线上。让O点在赤道面上围绕地心旋转2π,就可以将整个地球投影到圆柱面上了。
球面透视切投影,所谓球面透视,就是点O与球心的距离为地球的半径:
$$y=2R\tan\frac{\psi}{2}$$
$$c=R$$
球面透视割投影(ψk和-ψk纬线割,如果ψk=π/4,就是高尔投影):
$$y=R(1+\cos{\psi_k})\tan\frac{\psi}{2}$$
$$c=R\cos{\psi_k}$$
圆锥投影
圆锥投影的一般形式(极坐标),其中σ为圆锥常数,即圆锥展开后的扇形角度比上2π:
$$\begin{matrix}\rho = f(\psi )\ \delta =\sigma\lambda \end{matrix}$$
经线长度比m和纬线长度比n为
$$\begin{matrix}m = -\frac{d\rho}{Rd\psi}\ \frac{\sigma\rho}{R\cos\psi} \end{matrix}$$
等角圆锥投影:
$$\rho=\frac{K}{\tan^\sigma(\pi/4+\psi/2)}$$
K和σ依赖于投影更具体的性质:
单标准纬线ψ0的等角圆锥投影(即纬度ψ0处的纬线长度比为1),圆锥面切于这条纬线:
$$K=\frac{R\cos{\psi_0}\tan^\sigma(\pi/4+\psi/2)}{\sigma}$$
$$\sigma=\sin{\psi_0}$$
双标准纬线等角切投影(即纬度ψ1和ψ2处长度无变形),圆锥面割于这两条纬线:
$$K=\frac{R\cos{\psi_1}\tan^\sigma(\pi/4+\psi/2)}{\sigma}$$
$$\sigma=\frac{\lg (R\cos{\psi_1})-\lg(R\cos{\psi_2})}{\lg(\tan{\pi/4+\psi_2/2})-\lg(\tan{\pi/4+\psi_1/2})}$$
等面积圆锥投影
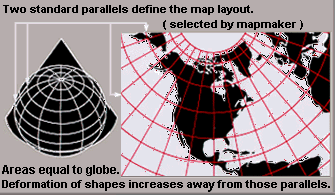
$$\rho=(\frac{2R^2}{\sigma}(K-\sin\psi))^{\frac{1}{2}}$$
切圆锥投影,切于ψ0:
$$K=\frac{1}{2}(\csc{\psi_0}+\sin{\psi_0})$$
$$\sigma=\sin{\psi_0}$$
割圆锥投影,割于ψ1和ψ2:
$$K=\frac{\sin{\psi_1}\cos^2{\psi_2}-\sin{\psi_2}\cos^2{\psi_2}}{\cos^2{\psi_2}-\cos^2{\psi_1}}$$
$$\sigma=\frac{\cos^2{\psi_2}-\cos^2{\psi_1}}{2(\sin{\psi_1}-\sin{\psi_2})}$$
等距离圆锥投影
$$\rho=K-R\rho$$
切圆锥投影,切于ψ0:
$$K=R\cot{\psi_0}+R\psi_0$$
$$\sigma=\sin{\psi_0}$$
割圆锥投影,割于ψ1和ψ2:
$$K=\frac{R\cos{\psi_1}}{\sigma}+R\psi_1$$
$$\sigma=\frac{\cos{\psi_2}-\cos{\psi_1}}{\psi_1-\psi_2}$$
正轴坐标转横轴,斜轴坐标
以方位投影为例,南北极轴是与投影面垂直。如果让任意一个轴与投影面垂直,那么就可以得到横轴或斜轴投影。那么,就只需要将点K的地理坐标(λ,ψ)转换为新极点Q(λ0,ψ0)下的球面极坐标(a,Z),然后按照正轴投影处理就可以了,如图所示,点P为北极点。
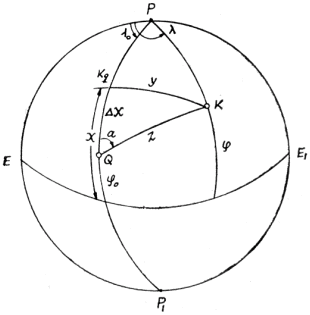
根据边QK的余弦定理可导出:
$$\cos Z=\sin\psi\sin{\psi_0}+\cos\psi\cos{\psi_0}\cos(\lambda - \lambda_0)$$
由于Z在0~π区间内,所以可以直接求出Z。
以QP作为换算后球面极坐标系下的“本初子午线”,求α:
根据边正弦和邻角余弦之积的定理,有:
$$\sin Z\cos \alpha = \sin\psi\cos{\psi_0}-\cos\psi\sin{\psi_0}\cos(\lambda - \lambda_0)$$
根据正弦定理:
$$\sin Z\sin\alpha=\cos\psi\sin(\lambda - \lambda_0)$$
这样,就可以将地理坐标转换为指定极点的球面极坐标了。获得的极坐标中Z可以很方便地转化(ψ=π/4-Z)为等效的“纬度”,以带入正轴投影公式。