Trie树的数组实现原理
Trie(Retrieval Tree)又称前缀树,可以用来保存多个字符串,并且非常便于查找。在trie中查找一个字符串的时间只取决于组成该串的字符数,与树的节点数无关。因此,它的查找速度通常比二叉搜索树更快。trie的结构很简单,每条边表示一个字符,从根节点到叶节点就可以表示一个完整的字符串。所以,如果用trie表示一组英文单词,就是一颗26叉数;表示一组自然数,就是一颗10叉树。直观上,实现trie很简单,比如实现英文单词的trie,使用如下的节点构造树:
:::c
struct node
{
char chr;
struct node *edges[26];
};这样做虽然简单,但没有很好的利用内存,edges数组肯定很多都是闲置的,如果使用到更多字符的话,这种浪费会更严重。这里介绍一种基于数组结构的trie实现方式,不仅节省内存,而且查询速度更快。基于数组查表的时间复杂度为O(|P|),基于平衡树的时间复杂度为O(|P|log|Σ|),其中,P表示查询的字符串长度,Σ表示字符集合。
基于数组的实现方式,把trie看作一个DFA,树的每个节点对应一个DFA状态,每条从父节点指向子节点的有向边对应一个DFA变换。遍历从根节点开始,字符串的每个字符作为输入用来确定下一个状态,直到叶节点。
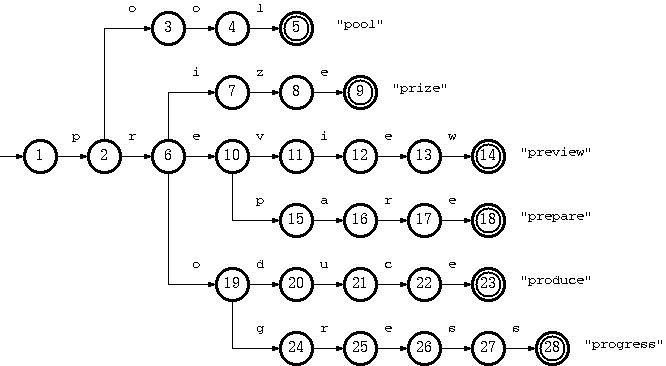
三数组trie
trie可以用三个数组来表示:
base: 其中的每个元素对应trie上的一个节点,即DFA的状态。对于节点s,base[s]是next和check在状态转换表中的起始位置。如果base[i]为负值或没有next转换,表示该状态为一个词语。next: 和check搭配使用,提供数据池分配稀疏向量,用于保存trie状态转换表的各行数据。来自各个节点的转换向量保存在此数组中。check: 与next平行使用,它与next相同位置的元素记录了next中对应元素的拥有者,即之前的状态。
所谓trie*状态转换表,即状态转换矩阵,是DFA里的概念:横行是状态转换向量*,比如,状态s接受n种输入字符c1,...,cn,即构成状态s的状态转换向量;纵列是各种状态,即trie的各节点。
对于输入字符c,从状态s转换到t,用三数组trie可以表示为:
check[base[s]+c] = s
next[base[s]+c] = t类似下图: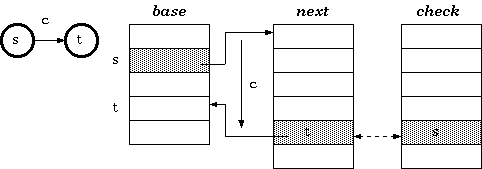
遍历树
对于给定状态s和输入字符c的遍历算法表示如下:
t := base[s]+c
if check[t] = s then
next state := next[t]
else
fail
endif创建树
当插入一个状态转换,比如,输入字符c,状态从s转换到t,此时,数组元素next[base[s]+c]]应该是空的,否则,整个占用该数组元素位置的状态转换向量或者状态s的状态转换向量必须要重新迁移(relocate)。实际过程中选择代价较小的那个。假设迁移状态s的状态转换向量,重新分配的起始位置为b,整个过程很简单:
Relocate(s: 状态, b: next数组中新的起始位置)
begin
foreach 状态s后的每种输入字符c
begin
check[b+c] := s 标记前件状态
next[b+c] := next[base[s]+c] 复制原先的状态数据
check[base[s]+c] := none 释放原先的状态数据
end
base[s] := b 完成迁移
end新位置b的选择比较关键,应该避免迁移过程中再次发生冲突。整个过程如下图,实线表示迁移前,虚线表示迁移后: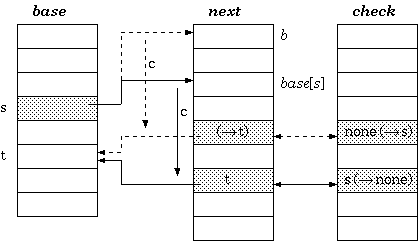
双数组trie
三数组trie的next和check数组元素之间存在间隙,可以将base和next合并,把base数组中的表示穿插在next中进行,而next中有值的项直接表示为base的内容,这样就得到两个平行的数组base和check,即双数组trie。
对于输入字符c,从状态s转换到t,用双数组trie可以表示为:
check[base[s]+c] = s
base[s]+c =t类似下图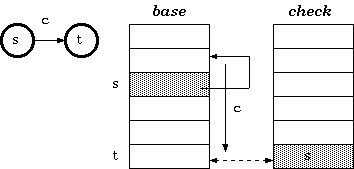
遍历
对于给定状态s和输入字符c的遍历算法表示如下:
t := base[s] + c;
if check[t] = s then
next state := t
else
fail
endif创建树
双数组trie的创建类似三数组trie,但重新迁移方法略有不同:
Relocate(s: 状态, s: base数组中的起始位置)
begin
foreach 状态s后的每种输入字符c
begin
check[b+c] := s 标记前件状态
base[b+c] := base[base[s}+c] 复制原先的状态数据
foreach 状态base[s]+c后的每种输入字符d
begin
check[base[base[s]+c]+d] := b+c
end
check[base[s]+c] := none 释放原先的状态数据
end
base[s] := b 完成迁移
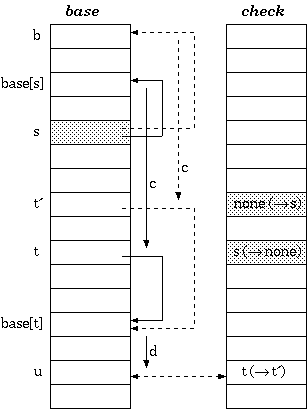
end整个过程如下图:
参考
http://blog.jqian.net/post/trie.html