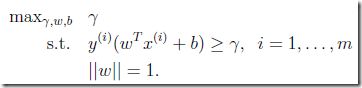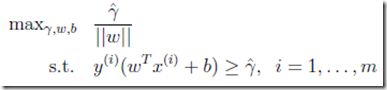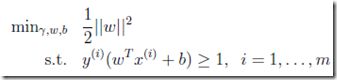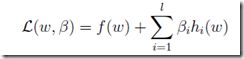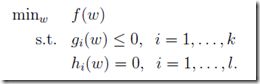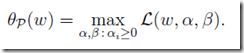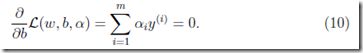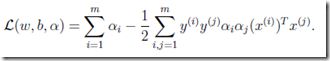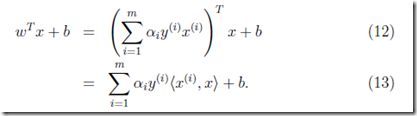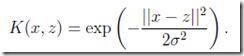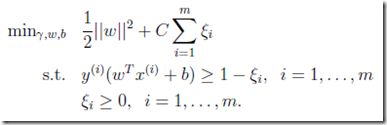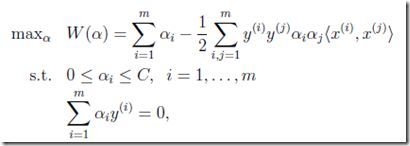Andrew Ng机器学习公开课笔记 -- 支持向量机
网易公开课,第6,7,8课
notes,http://cs229.stanford.edu/notes/cs229-notes3.pdf
SVM-支持向量机算法概述, 这篇讲的挺好,可以参考
先继续前面对线性分类器的讨论,
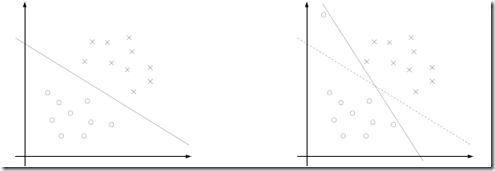
通过机器学习算法找到的线性分类的线,不是唯一的,对于一个训练集一般都会有很多线可以把两类分开,这里的问题是我们需要找到best的那条线
首先需要定义Margin,
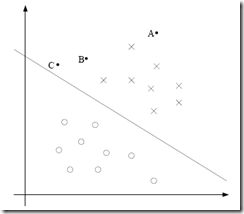
直观上来讲,best的那条线,应该是在可以正确分类的前提下,离所有的样本点越远越好,why?
因为越靠近分类线,表示该点越容易被分错,比如图中的C点,此时y=1,但是只要分类线略微调整一下角度,就有可能被分为y=-1
但对于A点,就可以非常confident的被分为y=1
所以分类线越远离样本点,表示我们的分类越confident
那么如果定义“远”这个概念?
functional margin
图中的分类线为,wx+b=0
那么点离这条线越远,有wx+b>>0或<<0,比如A点
所以functional margin定义为,前面加上y保证距离非负 ![]() ,y取值{-1,1}
,y取值{-1,1}
可以看出当点离线越远时,这个margin会越大,表示分类越confident
并且margin>0时,证明这个点的分类是正确的
因为比如训练集中y=1,而由线性分类器wx+b得到的结果-0.8,这样表示分错了,margin一定是<0的
对于训练集中m的样本,有 ![]()
即,整体的margin由最近的那个决定
如果要用functional margin来寻找best分类线,
那么我就需要找到使得 ![]() 最大的那条线
最大的那条线
但使用functional margin有个问题,因为你可以看到![]() 取决于w和b的值,你可以在不改变分类线的情况下,无限增加w和b的值,因为2x+1=0和4x+2=0是同一条线,但得到的functional margin却不一样
取决于w和b的值,你可以在不改变分类线的情况下,无限增加w和b的值,因为2x+1=0和4x+2=0是同一条线,但得到的functional margin却不一样
geometric margins
再来看另外一种margin,从几何角度更加直观的表示“远”
即该点到线的垂直距离,比如图中A到线的距离![]()
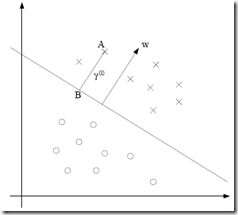
现在问题是,如何可以求解出![]()
可以看到A和分类线垂直相交于B,B是满足wx+b=0的等式的
所以我们通过A的x和![]() ,推导出B的x,最终通过等式求出
,推导出B的x,最终通过等式求出![]()
于是有, ![]()
求得, 
考虑y=-1的情况,最终得到如下, 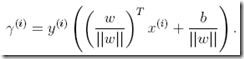
可以看到,如果||w|| = 1,那么functional margin 等于geometric margin
那么对于geometric margin,无论w,b的取值都不会改变margin的值,其实就是对functional margin做了norm化
The optimal margin classifier
先简单看看凸优化的概念
凸优化问题
用一个比较通俗的方式理解
为什么要凸优化?
这种优化是一定可以找到全局最优的,因为不存在局部最优,只有一个最优点
所以对于梯度下降或其他的最优化算法而言,在非凸的情况下,很可能找到的只是个局部最优凸集,http://en.wikipedia.org/wiki/Convex_set
很好理解,对于二维的情况比较形象,作为例子
集合中任意两点的连线都在集合中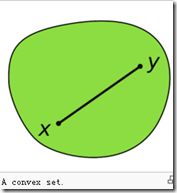
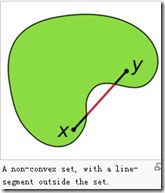
凸函数,http://en.wikipedia.org/wiki/Convex_function
函数图上任意两点的连线都在above这个图(这个应该取决于上凸或下凸,都below也一样)
the line segment between any two points on the graph of the function lies above the graph换个说法,就是他的epigraph是个凸集,其中epigraph就是the set of points on or above the graph of the function
its epigraph (the set of points on or above the graph of the function) is a convex set

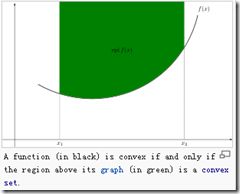
典型的凸函数,如quadratic function and the exponential function for any real number x凸优化问题的定义
在凸集上寻找凸函数的全局最值的过程称为凸优化
即,目标函数(objective function)是凸函数,可行集(feasible set)为凸集
接着看这个问题,根据上面的说法,要找到最优的classifier就是要找到geometric margin最大的那个超平面
即,最大化geometric margin ![]() ,并且训练集中所有样本点的geometric margin都大于这个
,并且训练集中所有样本点的geometric margin都大于这个![]() (因为
(因为![]() )
)
这里假设||w||=1,所以function margin等同于geometric margin,这里用的是function margin的公式
这个优化的问题是,约束||w||=1会导致非凸集,想想为什么?
所以要去掉这个约束,得到
其实改变就是将![]() 替换成
替换成![]() ,因为约束||w||=1就是为了保证
,因为约束||w||=1就是为了保证![]() =
=![]() ,所以替换后就可以直接去掉这个约束
,所以替换后就可以直接去掉这个约束
但这个优化仍然有问题,目标函数![]() 不是凸函数,因为是双曲线,明显非凸
不是凸函数,因为是双曲线,明显非凸
继续,由于function margin通过w,b的缩放可以是任意值,
所以增加约束,![]() ,这个约束是成立,因为无论
,这个约束是成立,因为无论![]() 得到什么值,通过w,b都除以
得到什么值,通过w,b都除以![]() ,就可以使
,就可以使![]()
为什么要加上平方,因为二次函数是典型的凸函数,所以这样就把非凸函数转换为凸函数
最终得到,
这是一个凸优化问题,可以用最优化工具去解
Lagrange duality
先偏下题,说下拉格朗日乘数法,为什么要说这个?
因为我们在上面看到这种极值问题是带约束条件的,这种极值问题如何解?好像有些困难
拉格朗日乘数法就是用来解决这种极值问题的,将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题
参考http://zh.wikipedia.org/wiki/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9%98%E6%95%B0
定义, 对于如下的极值问题,求最小化的f(w),同时需要满足i个约束条件h(w)
利用拉格朗日数乘法,变成如下的极值问题
其中![]() 称为Lagrange multipliers(拉格朗日算子)
称为Lagrange multipliers(拉格朗日算子)
最终,求这个方程组 
解出w和拉格朗日算子β,求出f(w)的极值
再看看wiki上的例子,好理解一些
假设有函数:,要求其极值(最大值/最小值),且满足条件
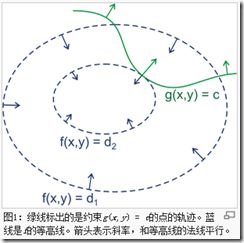
看图,画出f(x,y)的等高线,和约束条件g(x,y)=c的路径,会有多处相交
但只有当等高线和约束条件线相切的时候, 才是极值点
因为如果是相交,你想象沿着g(x,y)=c继续前进,一定可以到达比现在f值更高或更低的点
那么求相切点,就是求解f和g的偏导为0的方程组
说到这里,还不够,因为你发现上面的约束条件是不等式。。。
于是继续看更通用化的拉格朗日数乘法
既有等式,也有不等式的约束,称为generalized Lagrangian
这里先引入primal optimization problem
这个啥意思?
这里注意观察,当约束条件不满足时,这个式子一定是无穷大,因为如果g>0或h不等于0,那么只需要无限增大![]() ,那么L的最大值一定是无限大, 而只要满足约束条件, 那么L的最大值就是f
,那么L的最大值一定是无限大, 而只要满足约束条件, 那么L的最大值就是f
所以,primal optimization problem就等价于最开始的minf(), 并且primal optimization problem是没有约束条件的,因为已经隐含了约束条件
min的那个一定不是无穷大,所以一定是满足约束条件的
再引入dual optimization problem
而且可以看到和prime问题不一样的只是交换了min和max的顺序
并且简单可以证明,
这不是L的特殊特性,而是对于任意函数maxmin都是小于等于minmax的,可以随便找个试试呵呵
并且在特定的条件下,
这样我们就可以解dual问题来替代prime问题
为何这么麻烦?要引入dual问题,因为后面会看到dual问题有比较有用的特性,求解会比较简单
前面说了,只有在特定条件下,才可以用dual问题替代prime问题
那么这条件是什么?这些条件先列在这里,不理解没事
Suppose f and the gi’s are convex, and the hi’s are affine.
所有g函数为凸函数,而h函数为affine,所谓affine基本等同于linear,![]() ,只是多了截距b
,只是多了截距b
Suppose further that the constraints gi are (strictly) feasible; this means that there exists some w so that gi(w) < 0 for all i.
意思应该是,存在w可以让g约束成立的,即g是严格可行的
Under our above assumptions, there must exist w∗, α∗, β∗ so that w∗ is the solution to the primal problem, α∗, β∗ are the solution to the dual problem, and moreover p∗ = d∗ = L(w∗, α∗, β∗). Moreover, w∗, α∗ and β∗ satisfy the Karush-Kuhn-Tucker (KKT) conditions, which are as follows:
满足上面的假设后,就一定存在w∗, α∗, β∗满足p∗ = d∗ = L(w∗, α∗, β∗),并且这时的w∗, α∗ and β∗ 还满足KKT条件,
并且,只要任意w∗, α∗ and β∗满足KKT条件,那么它们就是prime和dual问题的解
注意其中的(5), 称为KKT dual complementarity condition
要满足这个条件,α和g至少有一个为0,当α>0时,g=0,这时称“gi(w) ≤ 0” constraint is active,因为此时g约束由不等式变为等式
在后面可以看到这意味着什么?g=0时是约束的边界,对于svm就是那些support vector
Optimal margin classifiers – Continuing
谈论了那么多晦涩的东西,不要忘了目的,我们的目的是要求解optimal margin 问题,所以现在继续
其中,g约束表示为, ![]()
那么什么时候g=0?当functional margin为1(前面描述optimal margin问题的时候,已经假设funtional margin为1)
所以只有靠近超平面最近的点的functional margin为1,即g=0,而其他训练点的functional margin都>1
该图中只有3个点满足这个条件,这些点称为support vector,只有他们会影响到分类超平面
实现在训练集中只有很少的一部分数据点是support vector,而其他的绝大部分点其实都是对分类没有影响的

前面说了半天prime问题和dual问题,就是为了可以用解dual问题来替代解prime问题
用dual问题的好处之一是,求解过程中只需要用到inner product![]() ,而表示直接使用x,这个对使用kernel解决高维度问题很重要
,而表示直接使用x,这个对使用kernel解决高维度问题很重要
好,下面就来求解optimal margin的dual问题, 
和上面讨论的广义拉格朗日相比,注意符号上的两个变化,
w变量—>w,b两个变量
只有α,而没有β,因为只有不等式约束而没有等式约束
对于dual问题,先求
![]()
这里就是对于w,b求L的min,做法就是求偏导为0的方程组
首先对w求偏导, ![]()
得到如下式子,这样我们在解出dual问题后,可以通过α,进一步算出w 
接着对b求偏导,得到下面的式子
现在把9,10,代入8,得到
于是有,第一个约束本来就有,第二个约束是对b求偏导得到的结果
You should also be able to verify that the conditions required for p∗ =d∗ and the KKT conditions (Equations 3–7) to hold are indeed satisfied in our optimization problem.
你可以verify我们这个问题是满足KKT条件的,所以可以解出这个dual问题来代替原来的prime问题
先不谈如何求解上面的极值问题(后面会介绍具体算法),我们先谈谈如果解出α,如何解出prime问题的w和b
w前面已经说过了,通过等式9就可以解出
那么如何解出b,
其实理解就是, 找出-1和1中靠超平面最近的点,即支持向量,用他们的b的均值作为b*
因为w定了,即超平面的方向定了,剩下的就是平移,平移到正负支持向量的中间位置为最佳
再想的多点,求出w,b后,我们的支持向量机就已经ready了,下面可以对新的数据点进行分类
很简单其实只要代入![]() ,-1或1来区分不同的类
,-1或1来区分不同的类
你可能觉得多此一举,这样每次分类都要把训练集都遍历一遍
其实无论是使用dual优化问题或是这里,都是为了避免直接计算x,而是代替的计算x的内积,因为后面谈到kernel,对于高维或无限维数据直接计算x是不可行的,而我们可以使用kernel函数来近似计算x的内积,这是后话
而且其实,这里的计算量并不大,因为前面介绍了,α只有支持向量是不为0的,而支持向量是很少的一部分
Kernels
先谈谈feature mapping,
比如想根据房屋的面积来预测价格,设范围面积为x,出于便于分类的考虑可能不光简单的用x,而是用![]() 做为3个feature
做为3个feature
其实将低维数据映射到高维数据的主要原因是,因为一些在低维度线性不可分的数据,到了高维度就是线性可分的了
没找到合适的图,想想在二维上看不可分的,到3维或更高维,也许就比较容易用一个超平面划分,这是合理的
这里我们称,"original” input value(比如x)为input attributes
称new quantities(![]() ) 为input features
) 为input features
We will also let φ denote the feature mapping, 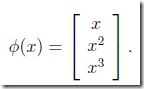
在将低维度的x mapping到高维度的φ(x)后,只需要把φ(x)代入之前dual problem的式子求解就ok
但问题在于,之前dual problem的<x,z>是比较容易算的,但是高维度或无限维的<φ(x), φ(z)>是很难算出的,所以这里无法直接算
所以kernel函数出场,
我们可以通过计算kernel函数来替代计算<φ(x), φ(z)>,kernel函数是通过x,z直接算出的
所以往往都是直接使用kernel函数去替换<x,z>,将svm映射到高维,而其中具体的φ()你不用关心(因为计算φ本身就是很expensive的),你只要知道这个kernel函数确实对应于某一个φ()就可以
polynomial kernel
我们先看一个简单的kernel函数的例子,称为polynomial kernel(多项式核)
这个kernel是可以推导出φ()的, 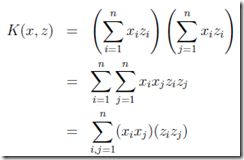
可以看出最终的结果是,φ将x mapping成xx,如下(假设n=3)
可见,如果这里如果直接计算![]() ,复杂度是
,复杂度是![]() ,因为x的维度为3,映射到φ就是9
,因为x的维度为3,映射到φ就是9
而计算K函数,复杂度就只有O(n)
推广一下,加上常数项
这个推导出的φ为,n=3
再推广一下,
![]() ,将x mapping到
,将x mapping到![]() ,虽然在
,虽然在![]() ,但是计算K仍然都是O(n)的
,但是计算K仍然都是O(n)的
虽然上面都找到了φ, 其实你根本不用关心φ是什么, 或者到底mapping到多高的维度
Gaussian kernel
在来看另外一种kernel函数,
来想一想内积的含义,当两个向量越相近的时候,内积值是越大的,而越远的时候,内积值是越小的
所以我们可以把kernel函数,看成是用来衡量两个向量有多相似
于是给出下面的kernel函数,这个函数由于描述x,z的相似度是合理的
(This kernel is called the Gaussian kernel, and corresponds to an infinite dimensional feature mapping φ.)
这个kernel函数对于的φ是个无限维的映射,你不用关心到底是什么
好到这里,自然有个问题?我随便找个函数就可以做kernel函数吗
如果判定一个kernel函数是否valid?即Can we tell if there is some feature mapping φ so that K(x, z) = φ(x)Tφ(z) for all x, z?
当然上面这个不太好操作,因为找到φ本身就是很困难的
下面就来证明一个判定方法,
假设,K is indeed a valid kernel corresponding to some feature mapping φ.
对于 consider some finite set of m points![]()
我们可以得到一个m-by-m的Kernel matrix K,其中 ![]() ,这里符号用重了,K同时表示kernel函数和kernel矩阵
,这里符号用重了,K同时表示kernel函数和kernel矩阵
于是可以证明,K是个半正定矩阵 (positive semi-definite)
(这个没有找到比较通俗易懂的解释方式,只知道定义是对于任何非0向量z,都有zTKz>=0,那么K称为半正定矩阵。谁可以通俗的解释一下) 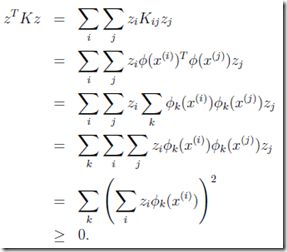
这里只证明必要条件,即K函数是valid kernel函数,那么K矩阵一定是半正定矩阵,其实这是个充分必要条件,即Mercer kernel的定义
所以有了这个定理,就比较方便了,你不用去找是否有对应的φ,只需要判定K矩阵是否为半正定矩阵即可
下面NG讲了个很典型的使用SVM kernel的例子,
For instance, consider the digit recognition problem, in which given an image (16x16 pixels) of a handwritten digit (0-9), we have to figure out
which digit it was.
就是根据16×16的像素点,来判断是否是0~9的数字
传统的方法是,神经网络本证明是解这个问题的最好的算法
可是这里用polynomial kernel or the Gaussian kernel,SVM也得到了很好的效果,和神经网络的结果一样好
这是很让人吃惊的,因为初始输入只是256维的向量,并且没有任何prior knowledge的情况下,可以得到和精心定制的神经网络一样好的效果
NG还讲了另外一个例子,即初始输入的维素不固定的情况下,例如输入字符串的长度不固定,如何产生固定的维数的输入,参考讲义吧呵呵
这里看到Kernel在SVM里面的应用已经非常清晰了,但是其实Kernel不是只是可以用于SVM
其实它是个通用的方法,只要学习算法可以只含有输入的内积,那么都可以使用kernel trick来替换它
For instance, this kernel trick can be applied with the perceptron to to derive a kernel perceptron algorithm.
Regularization and the non-separable case
讨论异常点,或离群点,比如下图,是否值得为了左上角那个点,将划分线调整成右边这样
从图上直观的看,应该不值得,右边的划分线远没有左边的合理,而且那个数据点很有可能是个异常点,可以忽略掉
we reformulate our optimization (using ℓ1 regularization) as follows:
其实就是加上修正值ξi,使得某些点的functional margin可以小于1,即容忍一些异常点
同时在目标函数上有做了相应的修正,
The parameter C controls the relative weighting between the twin goals of making the ||w||2 small (which we saw earlier makes the margin large) and of ensuring that most examples have functional margin at least 1.
列出拉格朗日,
最终得到的dual problem是,
和之前的相比,只是α的取值范围有了变化,现在还要<=C
对于这个dual problem的KKT dual-complementarity conditions变化为,
这个说的更清楚点,http://www.cnblogs.com/jerrylead/archive/2011/03/18/1988415.html
The SMO algorithm by John Platt
前面都是给出了dual problem,可是没有说怎么解,现在就来谈如何解SVM的dual problem
Coordinate ascent (descent)
坐标上升或下降,取决于求max或min
想法很简单,求解m维的最优问题
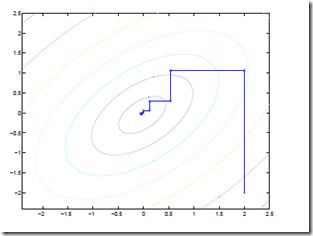
算法,不停迭代,每次迭代都是只改变某一个维度来做最优化,其他维度保持不变
这个算法从图上看起来就像这样,
前面学过梯度下降和牛顿法,有啥区别
牛顿,收敛很快,但每次收敛的代价比较大
坐标上升,收敛比较慢,但是每次收敛的代价都很小
梯度下降,不适合高维,因为每次迭代都需要算出梯度,需要考虑所有维度
SMO (sequential minimal optimization)
我们先再列出前面的dual优化问题,看看用坐标上升是否可解
注意到19这个约束,这个约束注定无法使用坐标上升
因为你如果只改变一个α值,就无法继续保证整个等式为0
因为在固定其他的α时,α1的值也是固定的
所以提出SMO算法,
想法也简单,既然单独改一个不行,我同时改两个α,就有可能仍然保持等式为0
The key reason that SMO is an efficient algorithm is that the update to αi, αj can be computed very efficiently.
下面就来看看SMO如何在每次迭代中高效的求的局部最优的α1和α2
上面的19可以改写成,

由于这个值是个常量,因为你要保持除α1和α2以外的都不变,所以写成
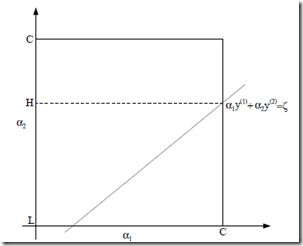
现在把α1和α2的约束用图表示出来,要保持约束就只能在这条线上移动,并且要满足<C
所以a2的取值在[L,H]
继续变换20,得到
代入目标函数,我们先求出α2,然后根据上面的式子算出α1
Treating α3, . . . , αm as constants, you should be able to verify that this is just some quadratic function in α2.
因为a3到am都是常数,你试着代入原来的W(), 会发现一定是得到α2的二次函数
即是这样的形式,
这个求极值,大家都应该没问题,很简单
问题是这样求出的极值点不一定在[L,H]的范围内
所以有,在范围内最好,不在范围内的话,也需要clip到范围内
There’re a couple more details that are quite easy but that we’ll leave you to read about yourself in Platt’s paper: One is the choice of the heuristics used to select the next αi, αj to update; the other is how to update b as the SMO algorithm is run.