[LeetCode] Rectangle Area 矩形面积

 

Find the total area covered by two rectilinear rectangles in a2D plane.

Each rectangle is defined by its bottom left corner and top right corner as shown in the figure.

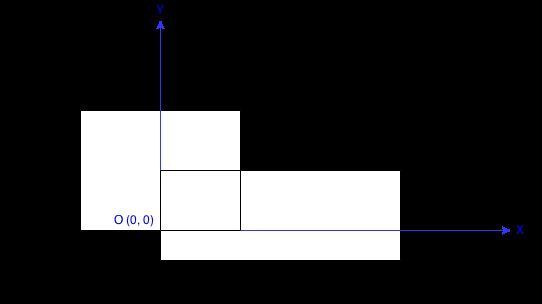
Assume that the total area is never beyond the maximum possible value of int.

Credits:
Special thanks to @mithmatt for adding this problem, creating the above image and all test cases.

 

这道题不算一道很难的题，但是我还是花了很久才做出来，刚开始我尝试找出所以有重叠的情况，发现有很多种情况，很麻烦。后来换了一种思路，尝试先找出所有的不相交的情况，只有四种，一个矩形在另一个的上下左右四个位置不重叠，这四种情况下返回两个矩形面积之和。其他所有情况下两个矩形是有交集的，这时候我们只要算出长和宽，即可求出交集区域的大小，然后从两个巨型面积之和中减去交集面积就是最终答案。求交集区域的长和宽也不难，由于交集都是在中间，所以横边的左端点是两个矩形左顶点横坐标的较大值，右端点是两个矩形右顶点的较小值，同理，竖边的下端点是两个矩形下顶点纵坐标的较大值，上端点是两个矩形上顶点纵坐标的较小值。代码如下：

 

class Solution {

public:

    int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {

        int sum = (C - A) * (D - B) + (H - F) * (G - E);

        if (E >= C || F >= D || B >= H || A >= G) return sum;

        return sum - ((min(G, C) - max(A, E)) * (min(D, H) - max(B, F)));

    }

};

 

当然，这三行还可以丧心病狂地合成一行，那么LeetCode中我遇见的第一次一行解题的方法如下所示：

 

class Solution {

public:

    int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {

        return (C - A) * (D - B) + (H - F) * (G - E) - (max((min(G, C) - max(A, E)), 0) * max((min(D, H) - max(B, F)), 0));

    }

};

 

LeetCode All in One 题目讲解汇总(持续更新中...)