A Brief Introduction About A-star Pathfinding Algorithm For Beginners
英文题目,汉语内容,有点挂羊头卖狗肉的嫌疑,不过请不要打击我这颗想学好英语的心。当了班主任我才发现大一18本书,11本是英语的,能多用两句英语就多用,个人认为这样也是积累的一种方法。
Thanks open source pioneers dedicated to computer science especially A*.
一、算法简介
为什么写这个,以前学长就用这个结合MFC做了个小游戏,分为三个等级“弱智,一般,大神”,分别采用不同算法来寻找迷宫出口,其中大神就是采用A*算法,当时感觉好神奇啊。前几天网上看到有人问A*算法,我就研究了下。下面的这部分内容估计奔走在各大高校的人工智能课上(国外的一片算法分析),很明显,笔者也不能免俗。
我知道下面不属于学术不端(没发表,结合自己的理解重新表达),现在就一起共享大神的作品吧(从图中可以看出并不是所有点都搜索一遍才找到了路径,给图片的目的是为了直观理解,以后忘记的话,看看图片也就记起来算法了,作为一名中共党员,笔者只信仰马克思主义,实践检验真理的唯一标准)。
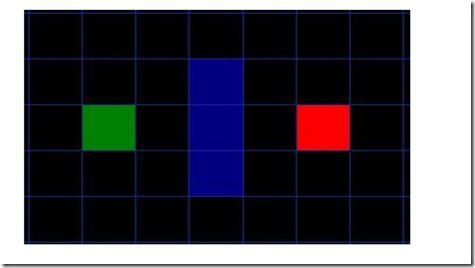
我们假设某个人要从A点到达B点,而一堵墙把这两个点隔开了,如下图所示,绿色部分代表起点A,红色部分代表终点B,蓝色方块部分代表之间的墙。
你首先会注意到我们把这一块搜索区域分成了一个一个的方格(如果地图特别大,类似稀疏矩阵的话就要结合数据结构的稀疏矩阵了,划分大块,不过没遇到过例子,不会),如此这般,使搜索区域简单化,正是寻找路径的第一步。这种方法将我们的搜索区域简化成了一个普通的二维数组。数组中的每一个元素表示对应的一个方格,该方格的状态被标记为可通过的和不可通过的。通过找出从A点到B点所经过的方格,就能得到AB之间的路径。当路径找出来以后,这个人就可以从一个格子中央移动到另一个格子中央,直到抵达目的地。 这些格子的中点叫做节点。当你在其他地方看到有关寻找路径的东西时,你会经常发现人们在讨论节点。为什么不直接把它们称作方格呢?因为你不一定要把你的搜索区域分隔成方块(感觉高大上),矩形、六边形或者其他任何形状都可以。况且节点还有可能位于这些形状内的任何一处呢(这句不懂,莫非是每个大块提前做一些预处理)?在中间、靠着边,或者什么的。我们就用这种设定,因为毕竟这是最简单的情况。
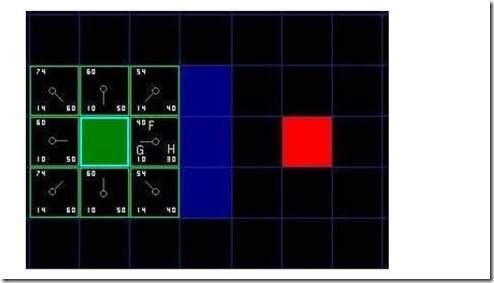
开始搜索,当我们把搜索区域简化成一些很容易操作的节点后,下一步就要构造一个搜索来寻找最短路径。在A*算法中,我们从A点开始,依次检查它的相邻节点,然后照此继续并向外扩展直到找到目的地。 从A点开始,将A点加入一个专门存放待检验的方格的“开放列表”中。这个开放列表有点像一张购物清单。当前这个列表中只有一个元素(个人感觉可以不加),但一会儿将会有更多。列表中包含的方格可能会是你要途经的方格,也可能不是。总之,这是一个包含待检验方格的列表。检查起点A相邻的所有可达的或者可通过的方格,不用管墙啊,水啊,或者其他什么无效地形,把它们也都加到开放列表中(这句话我很不认同,可能我理解错了,看我代码你会发现,我最外圈加了一圈1,表示墙壁,遇到墙壁就继续找其他相邻节点,并没有加入openTable)。对于每一个相邻方格,将点A保存为它们的“父方格”(类似最短路径算法打印路径,当然你可以选择严蔚敏老师的三维数组保存路径法,关于SP问题请参考笔者的(包括四大算法)http://www.cnblogs.com/hxsyl/p/3270401.html)。当我们要回溯路径的时候,父方格是一个很重要的元素。从开放列表中去掉方格A,并把A加入到一个“封闭列表”中。封闭列表存放的是你现在不用再去考虑的方格(说的很清楚,只是暂时不用考虑,如果不进行二次判断(指的是重新拿出来这个点来更新周边)的话,干嘛要closeTable,所以笔者认为不要光看理论,想一下实际情况,很多问题就会豁然开朗)。此时你将得到如图所示的样子。在这张图中,中间深绿色的方格是你的起始方格,所有相邻方格目前都在开放列表中,并且以亮绿色描边。每个相邻方格有一个灰色的指针指向它们的父方格,即起始方格。然后排序找到G最小的点作为下次起点。
下面还有很多,感觉不必赘述,随便百度一下都有的。
二、算法描述
1: //这段伪代码可以看出个大概,但是不完全,知道意思就行2: while (Open表非空) {3: 从Open中取得一个节点X,并从OPEN表中删除。4: if (X是目标节点) {5: 求得路径PATH;6: 返回路径PATH;7: }8: for (每一个X的子节点Y) {9: if (Y不在OPEN表和CLOSE表中) {10: 求Y的估价值;11: 并将Y插入OPEN表中;12: }else if (Y在OPEN表中) {13: if (Y的估价值小于OPEN表的估价值)14: 更新OPEN表中的估价值;15: }16: else {//Y在CLOSE表中17: if (Y的估价值小于CLOSE表的估价值) {18: 更新CLOSE表中的估价值;19: 从CLOSE表中移出节点,并放入OPEN表中;20: }21: }22: }23: 将X节点插入CLOSE表中;24: 按照估价值将OPEN表中的节点排序;25: }
三、算法Java实现
看了两天,感觉很简单,真正写的时候你会发现有多蛋疼,如果你是个爱思考的人,估计问题更多。
1: package util;2:3: import java.util.ArrayList;4: import java.util.Collections;5: import java.util.Stack;6:7: public class AstarPathFind {8: // 前四个是上下左右,后四个是斜角9: public final static int[] dx = { 0, -1, 0, 1, -1, -1, 1, 1 };10: public final static int[] dy = { -1, 0, 1, 0, 1, -1, -1, 1 };11:12: // 最外圈都是1表示不可通过13: final static public int[][] map = {14: { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 },15: { 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },16: { 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },17: { 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },18: { 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },19: { 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1 },20: { 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1 },21: { 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1 },22: { 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1 },23: { 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1 },24: { 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },25: { 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },26: { 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },27: { 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },28: { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 } };29:30: public static void main(String[] args) {31: // TODO Auto-generated method stub32: Point start = new Point(1, 1);33: Point end = new Point(10, 13);34: /*35: * 第一个问题:起点FGH需要初始化吗?36: * 看参考资料的图片发现不需要37: */38: Stack<Point> stack = printPath(start, end);39: if(null==stack) {40: System.out.println("不可达");41: }else {42: while(!stack.isEmpty()) {43: //输出(1,2)这样的形势需要重写toString44: System.out.print(stack.pop()+" -> ");45: }46: System.out.println();47: }48:49: }50:51: public static Stack<Point> printPath(Point start, Point end) {52:53: /*54: * 不用PriorityQueue是因为必须取出存在的元素55: */56: ArrayList<Point> openTable = new ArrayList<Point>();57: ArrayList<Point> closeTable = new ArrayList<Point>();58: openTable .clear();59: closeTable.clear();60: Stack<Point> pathStack = new Stack<Point>();61: start.parent = null;62: //该点起到转换作用,就是当前扩展点63: Point currentPoint = new Point(start.x, start.y);64: //closeTable.add(currentPoint);65: boolean flag = true;66:67: while(flag) {68: for (int i = 0; i < 8; i++) {69: int fx = currentPoint.x + dx[i];70: int fy = currentPoint.y + dy[i];71: Point tempPoint = new Point(fx,fy);72: if (map[fx][fy] == 1) {73: // 由于边界都是1中间障碍物也是1,,这样不必考虑越界和障碍点扩展问题74: //如果不设置边界那么fx >=map.length &&fy>=map[0].length判断越界问题75: continue;76: } else {77: if(end.equals(tempPoint)) {78: flag = false;79: //不是tempPoint,他俩都一样了此时80: end.parent = currentPoint;81: break;82: }83: if(i<4) {84: tempPoint.G = currentPoint.G + 10;85: }else {86: tempPoint.G = currentPoint.G + 14;87: }88: tempPoint.H = Point.getDis(tempPoint,end);89: tempPoint.F = tempPoint.G + tempPoint.H;90: //因为重写了equals方法,所以这里包含只是按equals相等包含91: //这一点是使用java封装好类的关键92: if(openTable.contains(tempPoint)) {93: int pos = openTable.indexOf(tempPoint );94: Point temp = openTable.get(pos);95: if(temp.F > tempPoint.F) {96: openTable.remove(pos);97: openTable.add(tempPoint);98: tempPoint.parent = currentPoint;99: }100: }else if(closeTable.contains(tempPoint)){101: int pos = closeTable.indexOf(tempPoint );102: Point temp = closeTable.get(pos);103: if(temp.F > tempPoint.F) {104: closeTable.remove(pos);105: openTable.add(tempPoint);106: tempPoint.parent = currentPoint;107: }108: }else {109: openTable.add(tempPoint);110: tempPoint.parent = currentPoint;111: }112:113: }114: }//end for115:116: if(openTable.isEmpty()) {117: return null;118: }//无路径119: if(false==flag) {120: break;121: }//找到路径122: openTable.remove(currentPoint);123: closeTable.add(currentPoint);124: Collections.sort(openTable);125: currentPoint = openTable.get(0);126:127: }//end while128: Point node = end;129: while(node.parent!=null) {130: pathStack.push(node);131: node = node.parent;132: }133: return pathStack;134: }135: }136:137: class Point implements Comparable<Point>{138: int x;139: int y;140: Point parent;141: int F, G, H;142:143: public Point(int x, int y) {144: super();145: this.x = x;146: this.y = y;147: this.F = 0;148: this.G = 0;149: this.H = 0;150: }151:152: @Override153: public int compareTo(Point o) {154: // TODO Auto-generated method stub155: return this.F - o.F;156: }157:158: @Override159: public boolean equals(Object obj) {160: Point point = (Point) obj;161: if (point.x == this.x && point.y == this.y)162: return true;163: return false;164: }165:166: public static int getDis(Point p1, Point p2) {167: int dis = Math.abs(p1.x - p2.x) * 10 + Math.abs(p1.y - p2.y) * 10;168: return dis;169: }170:171: @Override172: public String toString() {173: return "(" + this.x + "," + this.y + ")";174: }175:176: }177: /*178: 成功了,我在想找到的一定是最佳路线么,别告诉我因为每次取最佳点,我的意思是可能8次每循环完就break了,男刀这是不同路径的最佳路线179: */180:
四、结束语
大神提到,不管地图差异的话,主要是排序耽误时间,可考虑二叉堆(大神和我想法一样,哈哈),实际就是堆排序(不太清楚的请参考博主这篇博文http://www.cnblogs.com/hxsyl/p/3244756.html),不过这都不是咱么考虑的问题啦。。。。。好啦,洗洗该去上听力课了。
![]9Y1RQ_M~DNW[A8CED]BH4F ]9Y1RQ_M~DNW[A8CED]BH4F](http://img.e-com-net.com/image/product/08359cb04b5744029fcff5b20b0928a5.png)