二十四.基于机器学习的入侵检测和攻击识别——以KDD CUP99数据集为例
这是作者的系列网络安全自学教程,主要是关于网安工具和实践操作的在线笔记,特分享出来与博友共勉,希望您们喜欢,一起进步。前文分享了Web渗透的第一步工作,涉及网站信息、域名信息、端口信息、敏感信息及指纹信息收集。这篇文章换个口味,将分享机器学习在安全领域的应用,并复现一个基于机器学习的入侵检测和攻击识别。严格意义上来说,这篇文章是数据分析,它有几个亮点:
(1) 详细介绍了数据分析预处理中字符特征转换为数值特征、数据标准化、数据归一化,这都是非常基础的工作。
(2) 结合入侵检测应用KNN实现分类。
(3) 绘制散点图采用序号、最小欧式距离、类标,ROC曲线绘制都是之前没分享的。
文章中也有很多不足之处,恶意代码或入侵检测作者还会继续深入,包括源代码、二进制分析。作者作为网络安全的小白,分享一些自学基础教程给大家,希望你们喜欢。同时,更希望你能与我一起操作进步,作者的目标是分享网络安全自学系列100篇,争取能入门,后续也将深入学习网络安全和系统安全知识并分享相关实验。总之,希望该系列文章对博友有所帮助,写文不容易,大神请飘过,不喜勿喷,谢谢!
安全资源下载地址:https://github.com/eastmountyxz/NetworkSecuritySelf-study
恶意代码下载地址:https://github.com/eastmountyxz/AI-for-Malware-Analysis-
文章目录
- 一.KDD CUP背景知识
- 二.数据特征描述
- 1.TCP连接基本特征(共9种,序号1~9)
- 2.TCP连接的内容特征(共13种,序号10~22)
- 3.基于时间的网络流量统计特征 (共9种,序号23~31)
- 4.基于主机的网络流量统计特征 (共10种,序号32~41)
- 5.样本分析
- 三.Python数据处理
- 1.KDD 99数据集评价
- 2.字符型转换为数值型
- 四.KNN实现入侵检测
- 1.KNN
- 2.算法实现
- 五.入侵检测算法优化
- 1.数值标准化
- 2.数值归一化
- 3.KNN检测及评估
- 4.Github代码分享
- 六.总结
前文学习:
[网络安全自学篇] 一.入门笔记之看雪Web安全学习及异或解密示例
[网络安全自学篇] 二.Chrome浏览器保留密码功能渗透解析及登录加密入门笔记
[网络安全自学篇] 三.Burp Suite工具安装配置、Proxy基础用法及暴库示例
[网络安全自学篇] 四.实验吧CTF实战之WEB渗透和隐写术解密
[网络安全自学篇] 五.IDA Pro反汇编工具初识及逆向工程解密实战
[网络安全自学篇] 六.OllyDbg动态分析工具基础用法及Crakeme逆向破解
[网络安全自学篇] 七.快手视频下载之Chrome浏览器Network分析及Python爬虫探讨
[网络安全自学篇] 八.Web漏洞及端口扫描之Nmap、ThreatScan和DirBuster工具
[网络安全自学篇] 九.社会工程学之基础概念、IP获取、IP物理定位、文件属性
[网络安全自学篇] 十.论文之基于机器学习算法的主机恶意代码
[网络安全自学篇] 十一.虚拟机VMware+Kali安装入门及Sqlmap基本用法
[网络安全自学篇] 十二.Wireshark安装入门及抓取网站用户名密码(一)
[网络安全自学篇] 十三.Wireshark抓包原理(ARP劫持、MAC泛洪)及数据流追踪和图像抓取(二)
[网络安全自学篇] 十四.Python攻防之基础常识、正则表达式、Web编程和套接字通信(一)
[网络安全自学篇] 十五.Python攻防之多线程、C段扫描和数据库编程(二)
[网络安全自学篇] 十六.Python攻防之弱口令、自定义字典生成及网站暴库防护
[网络安全自学篇] 十七.Python攻防之构建Web目录扫描器及ip代理池(四)
[网络安全自学篇] 十八.XSS跨站脚本攻击原理及代码攻防演示(一)
[网络安全自学篇] 十九.Powershell基础入门及常见用法(一)
[网络安全自学篇] 二十.Powershell基础入门及常见用法(二)
[网络安全自学篇] 二十一.GeekPwn极客大赛之安全攻防技术总结及ShowTime
[网络安全自学篇] 二十二.Web渗透之网站信息、域名信息、端口信息、敏感信息及指纹信息收集
[网络安全自学篇] 二十三.基于机器学习的恶意请求识别及安全领域中的机器学习
前文欣赏:
[渗透&攻防] 一.从数据库原理学习网络攻防及防止SQL注入
[渗透&攻防] 二.SQL MAP工具从零解读数据库及基础用法
[渗透&攻防] 三.数据库之差异备份及Caidao利器
[渗透&攻防] 四.详解MySQL数据库攻防及Fiddler神器分析数据包
该篇文章参考了以下文献,非常推荐大家阅读这些大牛的文章:
[1] 机器学习在安全攻防场景的应用与分析 - 腾讯云FreeBuf官方
[2] 用机器学习玩转恶意URL检测 - 腾讯云FreeBuf官方
[3] https://github.com/exp-db/AI-Driven-WAF
[4] https://github.com/eastmountyxz
[5] 张思思, 左信, 刘建伟. 深度学习中的对抗样本问题[J]. 计算机学报,2019(8).
[6] KDD CUP 99数据集
[7] KDD CUP99数据集预处理(Python实现) CSDN Asia-Lee大神
[8] The 1998 Lincoln Laboratory IDS Evaluation A Critique. by John McHugh
[9] Testing Intrusion Detection Systems: A Critique of the 1998 and 1999 DARPA Intrusion Detection System Evaluations as Performed by Lincoln Laboratory. by John McHugh
[10] The Comparison of IP Networks. by ST Brugger
[11] KDD Cup ’99 dataset (Network Intrusion) considered harmful. by ST Brugger
[12] https://github.com/gongyanc/kddcup99
[13] https://blog.gongyan.me/2017/04/kdd-cup99/
[14] Python3实现常用数据标准化方法 - z小白
声明:本人坚决反对利用教学方法进行犯罪的行为,一切犯罪行为必将受到严惩,绿色网络需要我们共同维护,更推荐大家了解它们背后的原理,更好地进行防护。
一.KDD CUP背景知识
KDD是数据挖掘与知识发现(Data Mining and Knowledge Discovery)的简称,KDD CUP是由ACM(Association for Computing Machiner)的 SIGKDD(Special Interest Group on Knowledge Discovery and Data Mining)组织的年度竞赛。
”KDD CUP 99 dataset”是KDD竞赛在1999年举行时采用的数据集。从官网下载KDD99数据集,如下图所示:
http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html
KDD Cup 1999数据集: 是与KDD-99第五届知识发现和数据挖掘国际会议同时举行的第三届国际知识发现和数据挖掘工具竞赛使用的数据集。竞争任务是建立一个网络入侵检测器,这是一种能够区分称为入侵或攻击的“不良”连接和“良好”的正常连接的预测模型。该数据集包含一组要审核的标准数据,其中包括在军事网络环境中模拟的多种入侵。
数据文件包括:
kddcup.names 功能列表。
kddcup.data.gz 完整数据集(18M; 743M未压缩)
kddcup.data_10_percent.gz 10%的数据集(2.1M; 75M未压缩)
kddcup.newtestdata_10_percent_unlabeled.gz(1.4M; 45M未压缩)
kddcup.testdata.unlabeled.gz (11.2M; 430M未压缩)
kddcup.testdata.unlabeled_10_percent.gz (1.4M; 45M未压缩)
corrected.gz 正确标签的测试数据
training_attack_types 入侵类型列表
typo-correction.txt 关于数据集中的简要说明
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
1998年美国国防部高级规划署(DARPA)在MIT林肯实验室进行了一项入侵检测评估项目。林肯实验室建立了模拟美国空军局域网的一个网络环境,收集了9周时间的TCPdump()网络连接和系统审计数据,仿真各种用户类型、各种不同的网络流量和攻击手段,使它就像一个真实的网络环境。这些TCPdump采集的原始数据被分为两个部分:7周时间的训练数据,大概包含5,000,000多个网络连接记录,剩下的2周时间的测试数据大概包含2,000,000个网络连接记录。
一个网络连接定义为在某个时间内从开始到结束的TCP数据包序列,并且在这段时间内,数据在预定义的协议下(如TCP、UDP)从源IP地址到目的IP地址的传递。每个网络连接被标记为正常(normal)或异常(attack),异常类型被细分为4大类共39种攻击类型,其中22种攻击类型出现在训练集中,另有17种未知攻击类型出现在测试集中。
4种异常类型分别是:
- DOS(denial-of-service)拒绝服务攻击,例如ping-of-death, syn flood, smurf等。
- R2L(unauthorized access from a remote machine to a local machine)来自远程主机的未授权访问,例如guessing password。
- U2R(unauthorized access to local superuser privileges by a local unpivileged user)未授权的本地超级用户特权访问,例如buffer overflow attacks。
- PROBING(surveillance and probing) 端口监视或扫描,例如port-scan, ping-sweep等。
随后来自哥伦比亚大学的Sal Stolfo 教授和来自北卡罗莱纳州立大学的 Wenke Lee 教授采用数据挖掘等技术对以上的数据集进行特征分析和数据预处理,形成了一个新的数据集。该数据集用于1999年举行的KDD CUP竞赛中,成为著名的KDD99数据集。虽然年代有些久远,但KDD99数据集仍然是网络入侵检测领域的事实Benckmark,为基于计算智能的网络入侵检测研究奠定基础。
二.数据特征描述
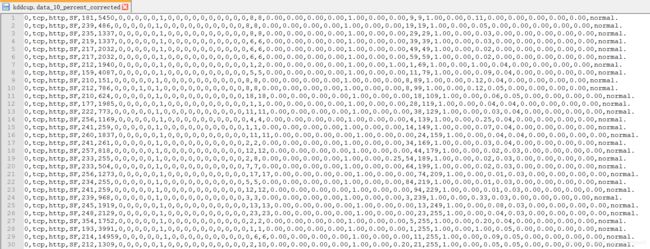
下载的数据集如下图所示,这里以10%的数据集来进行实验。
- kddcup.data_10_percent_corrected
- kddcup.testdata.unlabeled_10_percent
下面展现了其中3条记录,总共有42项特征,最后一列是标记特征(Label),其他前41项特征共分为四大类。
- TCP连接基本特征(共9种,序号1~9)
- TCP连接的内容特征(共13种,序号10~22)
- 基于时间的网络流量统计特征 (共9种,序号23~31)
- 基于主机的网络流量统计特征 (共10种,序号32~41)
0,tcp,http,SF,239,486,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,8,8,0.00,0.00,0.00,0.00,1.00,0.00,0.00,19,19,1.00,0.00,0.05,0.00,0.00,0.00,0.00,0.00,normal.
0,icmp,ecr_i,SF,1032,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,511,511,0.00,0.00,0.00,0.00,1.00,0.00,0.00,255,255,1.00,0.00,1.00,0.00,0.00,0.00,0.00,0.00,smurf.
0,tcp,private,S0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,52,13,1.00,1.00,0.00,0.00,0.25,0.10,0.00,255,13,0.05,0.07,0.00,0.00,1.00,1.00,0.00,0.00,neptune.
接下来按顺序解释各个特征的具体含义,这是进行数据分析之前非常必要的一个环节。
1.TCP连接基本特征(共9种,序号1~9)
基本连接特征包含了一些连接的基本属性,如连续时间,协议类型,传送的字节数等。
- (1) duration - 连接持续时间,以秒为单位,连续类型。范围是 [0, 58329] 。它的定义是从TCP连接以3次握手建立算起,到FIN/ACK连接结束为止的时间;若为UDP协议类型,则将每个UDP数据包作为一条连接。数据集中出现大量的duration = 0 的情况,是因为该条连接的持续时间不足1秒。
- (2) protocol_type - 协议类型,离散类型,共有3种:TCP, UDP, ICMP。
- (3) service - 目标主机的网络服务类型,离散类型,共有70种。’aol’, ‘auth’, ‘bgp’, ‘courier’, ‘csnet_ns’, ‘ctf’, ‘daytime’, ‘discard’, ‘domain’, ‘domain_u’, ‘echo’, ‘eco_i’, ‘ecr_i’, ‘efs’, ‘exec’, ‘finger’, ‘ftp’, ‘ftp_data’, ‘gopher’, ‘harvest’, ‘hostnames’, ‘http’, ‘http_2784′, ‘http_443′, ‘http_8001′, ‘imap4′, ‘IRC’, ‘iso_tsap’, ‘klogin’, ‘kshell’, ‘ldap’, ‘link’, ‘login’, ‘mtp’, ‘name’, ‘netbios_dgm’, ‘netbios_ns’, ‘netbios_ssn’, ‘netstat’, ‘nnsp’, ‘nntp’, ‘ntp_u’, ‘other’, ‘pm_dump’, ‘pop_2′, ‘pop_3′, ‘printer’, ‘private’, ‘red_i’, ‘remote_job’, ‘rje’, ‘shell’, ‘smtp’, ‘sql_net’, ‘ssh’, ‘sunrpc’, ‘supdup’, ‘systat’, ‘telnet’, ‘tftp_u’, ‘tim_i’, ‘time’, ‘urh_i’, ‘urp_i’, ‘uucp’, ‘uucp_path’, ‘vmnet’, ‘whois’, ‘X11′, ‘Z39_50′。
- (4) flag - 连接正常或错误的状态,离散类型,共11种。’OTH’, ‘REJ’, ‘RSTO’, ‘RSTOS0′, ‘RSTR’, ‘S0′, ‘S1′, ‘S2′, ‘S3′, ‘SF’, ‘SH’。它表示该连接是否按照协议要求开始或完成。例如SF表示连接正常建立并终止;S0表示只接到了SYN请求数据包,而没有后面的SYN/ACK。其中SF表示正常,其他10种都是error。
- (5) src_bytes - 从源主机到目标主机的数据的字节数,连续类型,范围是 [0, 1379963888]。
- (6) dst_bytes - 从目标主机到源主机的数据的字节数,连续类型,范围是 [0. 1309937401]。
- (7) land - 若连接来自/送达同一个主机/端口则为1,否则为0,离散类型,0或1。
- (8) wrong_fragment - 错误分段的数量,连续类型,范围是 [0, 3]。
- (9) urgent - 加急包的个数,连续类型,范围是[0, 14]。
2.TCP连接的内容特征(共13种,序号10~22)
对于U2R和R2L之类的攻击,由于它们不像DoS攻击那样在数据记录中具有频繁序列模式,而一般都是嵌入在数据包的数据负载里面,单一的数据包和正常连接没有什么区别。为了检测这类攻击,Wenke Lee等从数据内容里面抽取了部分可能反映入侵行为的内容特征,如登录失败的次数等。
- (10) hot - 访问系统敏感文件和目录的次数,连续,范围是 [0, 101]。例如访问系统目录,建立或执行程序等。
- (11) num_failed_logins - 登录尝试失败的次数。连续,[0, 5]。
- (12) logged_in - 成功登录则为1,否则为0,离散,0或1。
- (13) num_compromised - compromised条件出现的次数,连续,[0, 7479]。
- (14) root_shell - 若获得root shell 则为1,否则为0,离散,0或1。root_shell是指获得超级用户权限。
- (15) su_attempted - 若出现”su root” 命令则为1,否则为0,离散,0或1。
- (16) num_root - root用户访问次数,连续,[0, 7468]。
- (17) num_file_creations - 文件创建操作的次数,连续,[0, 100]。
- (18) num_shells - 使用shell命令的次数,连续,[0, 5]。
- (19) num_access_files - 访问控制文件的次数,连续,[0, 9]。例如对 /etc/passwd 或 .rhosts 文件的访问。
- (20) num_outbound_cmds - 一个FTP会话中出站连接的次数,连续,0。数据集中这一特征出现次数为0。
- (21) is_hot_login - 登录是否属于“hot”列表,是为1,否则为0,离散,0或1。例如超级用户或管理员登录。
- (22) is_guest_login - 若是guest 登录则为1,否则为0,离散,0或1。
3.基于时间的网络流量统计特征 (共9种,序号23~31)
由于网络攻击事件在时间上有很强的关联性,因此统计出当前连接记录与之前一段时间内的连接记录之间存在的某些联系,可以更好的反映连接之间的关系。这类特征又分为两种集合:一个是 “same host”特征,只观察在过去两秒内与当前连接有 相同目标主机 的连接,例如相同的连接数,在这些相同连接与当前连接有相同的服务的连接等等;另一个是 “same service”特征,只观察过去两秒内与当前连接有 相同服务 的连接,例如这样的连接有多少个,其中有多少出现SYN错误或者REJ错误。
- (23) count - 过去两秒内,与当前连接具有相同的目标主机的连接数,连续,[0, 511]。
- (24) srv_count - 过去两秒内,与当前连接具有相同服务的连接数,连续,[0, 511]。
- (25) serror_rate - 过去两秒内,在与当前连接具有相同目标主机的连接中,出现“SYN” 错误的连接的百分比,连续,[0.00, 1.00]。
- (26) srv_serror_rate - 过去两秒内,在与当前连接具有相同服务的连接中,出现“SYN” 错误的连接的百分比,连续,[0.00, 1.00]。
- (27) rerror_rate - 过去两秒内,在与当前连接具有相同目标主机的连接中,出现“REJ” 错误的连接的百分比,连续,[0.00, 1.00]。
- (28) srv_rerror_rate - 过去两秒内,在与当前连接具有相同服务的连接中,出现“REJ” 错误的连接的百分比,连续,[0.00, 1.00]。
- (29) same_srv_rate - 过去两秒内,在与当前连接具有相同目标主机的连接中,与当前连接具有相同服务的连接的百分比,连续,[0.00, 1.00]。
- (30) diff_srv_rate - 过去两秒内,在与当前连接具有相同目标主机的连接中,与当前连接具有不同服务的连接的百分比,连续,[0.00, 1.00]。
- (31) srv_diff_host_rate - 过去两秒内,在与当前连接具有相同服务的连接中,与当前连接具有不同目标主机的连接的百分比,连续,[0.00, 1.00]。
注意:这一大类特征中,23、25、27、29、30这5个特征是 “same host” 特征,前提都是与当前连接具有相同目标主机的连接;24、26、28、31这4个特征是 “same service” 特征,前提都是与当前连接具有相同服务的连接。
4.基于主机的网络流量统计特征 (共10种,序号32~41)
基于时间的流量统计只是在过去两秒的范围内统计与当前连接之间的关系,而在实际入侵中,有些 Probing攻击使用慢速攻击模式来扫描主机或端口,当它们扫描的频率大于2秒的时候,基于时间的统计方法就无法从数据中找到关联。所以Wenke Lee等按照目标主机进行分类,使用一个具有100个连接的时间窗,统计当前连接之前100个连接记录中与当前连接具有 相同目标主机 的统计信息。
- (32) dst_host_count - 前100个连接中,与当前连接具有相同目标主机的连接数,连续,[0, 255]。
- (33) dst_host_srv_count - 前100个连接中,与当前连接具有相同目标主机相同服务的连接数,连续,[0, 255]。
- (34) dst_host_same_srv_rate - 前100个连接中,与当前连接具有相同目标主机相同服务的连接所占的百分比,连续,[0.00, 1.00]。
- (35) dst_host_diff_srv_rate - 前100个连接中,与当前连接具有相同目标主机不同服务的连接所占的百分比,连续,[0.00, 1.00]。
- (36) dst_host_same_src_port_rate - 前100个连接中,与当前连接具有相同目标主机相同源端口的连接所占的百分比,连续,[0.00, 1.00]。
- (37) dst_host_srv_diff_host_rate - 前100个连接中,与当前连接具有相同目标主机相同服务的连接中,与当前连接具有不同源主机的连接所占的百分比,连续,[0.00, 1.00]。
- (38) dst_host_serror_rate - 前100个连接中,与当前连接具有相同目标主机的连接中,出现SYN错误的连接所占的百分比,连续,[0.00, 1.00]。
- (39) dst_host_srv_serror_rate - 前100个连接中,与当前连接具有相同目标主机相同服务的连接中,出现SYN错误的连接所占的百分比,连续,[0.00, 1.00]。
- (40) dst_host_rerror_rate - 前100个连接中,与当前连接具有相同目标主机的连接中,出现REJ错误的连接所占的百分比,连续,[0.00, 1.00]。
- (41) dst_host_srv_rerror_rate - 前100个连接中,与当前连接具有相同目标主机相同服务的连接中,出现REJ错误的连接所占的百分比,连续,[0.00, 1.00]。
5.样本分析
Wende Lee等人在处理原始连接数据时将部分重复数据去除,例如进行DoS攻击时产生大量相同的连接记录,就只取攻击过程中5分钟内的连接记录作为该攻击类型的数据集。同时,也会随机抽取正常(normal)数据连接作为正常数据集。KDD99数据集总共由500万条记录构成,它还提供一个10%的训练子集和测试子集,它的样本类别分布如下:
- NORMAL:正常访问,训练集(10%)有97278个样本,测试集(Corrected)有60593个样本。
- PROBE: 端口监视或扫描,训练集(10%)有4107个样本,测试集(Corrected)有4166个样本。攻击包括: ipsweep、 mscan、nmap、portsweep、saint、satan。
- DOS:拒绝服务攻击,训练集(10%)有391458个样本,测试集(Corrected)有229853个样本。攻击包括: apache2、back、land、mailbomb、neptune、pod、processtable、smurf、teardrop、udpstorm。
- U2R:未授权的本地超级用户特权访问,训练集(10%)有52个样本,测试集(Corrected)有228个样本。攻击包括:buffer_overflow、httptunnel、loadmodule、perl、ps、rootkit、sqlattack、 xterm。
- R2L:来自远程主机的未授权访问,训练集(10%)有1126个样本,测试集(Corrected)有16189个样本。攻击包括:ftp_write、guess_passwd、imap、multihop、named、phf、sendmail、snmpgetattack、snmpguess、spy、warezclient、warezmaster、worm、xlock、xsnoop。
注意:
(1) KDD99将攻击类型分为4类,然后又细分为39小类,每一类代表一种攻击类型,类型名被标记在训练数据集每一行记录的最后一项。
(2) 某些攻击类型只在测试集(或训练集)中出现,而未在训练集(或测试集)中出现。比如10%的数据集中,训练集中共出现了22个攻击类型,而剩下的17种只在测试集中出现,这样设计的目的是检验分类器模型的泛化能力,对未知攻击类型的检测能力是评价入侵检测系统好坏的重要指标。
三.Python数据处理
1.KDD 99数据集评价
入侵检测
入侵检测的方法从根本上讲就是设计一个分类器,能将数据流中的正常与异常数据区分出来,从而实现对攻击行为的报警。本文KDD99数据集的目的就是为入侵检测系统提供统一的性能评价基准,常用来在学术圈检验入侵检测算法的好坏。本文将数据集中的10%训练集来训练分类器,然后用corrected测试集测试分类器性能,这个分类器可以是基于贝叶斯的、决策树的、神经网络的或者是支持向量机的。
特征选择
特征选择是KDD99数据集的另一个主要应用。KDD99数据集中,每个连接有41个特征,对于一个分类器来说,要从这么多特征中提取规则是费时且不精确的,这体现在一些无关或冗余的特征往往会降低分类器模型的检测精度和速度。而且对于从原始的tcpdump数据中提取特征这一过程,也将是困难和费时的,这对于在线入侵检测系统是致命的。因此去除冗余特征或不重要特征,对于提高分类器训练速度和检测精度来说,是必要的。要说明的是对于不同的分类器来说,最优的特征子集可以是不同的。
数据集评价
KDD 99数据集是入侵检测领域的Benchmark(基准),为基于计算智能的网络入侵检测研究奠定了基础,从那以后很多学者开始研究入侵检测算法,当然不能不提到众所周知的“功夫网”,实际上它就是一个大规模的入侵检测系统。KDD99从1999年创建已经过去多年,当年的实验条件和攻击手段放到今天早已过时,而且从原来的网络层攻击进化为针对应用层的攻击,例如跨站脚本、数据库注入等等(当然,针对应用层攻击自有新的解决方案)。你可以说,要解决这个问题,重新做一遍98年那个实验,用新的设备新的攻击手段,产生新的数据集不就行了吗?事实是据我所知还没有学术组织公开新的且质量较高的数据集,安全软件公司里肯定有足够的数据库,当然,人家是不会共享出来的,就靠这个赚钱。另一个解决办法是你自己搭建网络环境,自己做实验,就是累点,当然可行。
所以,希望这篇基础性文章对您有所帮助。
2.字符型转换为数值型
在数据挖掘的过程中,数据的预处理一直都是非常重要的一个环节,只有把数据转化为分类器认可的形式才可以对其进行训练。下面这段代码参考CSDN asialee_bird大神的文章及Github代码,非常厉害的一位博主,推荐大家阅读他的文章(https://blog.csdn.net/asialee_bird)。
个人认为这段代码最大的亮点是:
(1) 有效地将数据集中字符型转换为数值型,这是数据集预处理常见的方法。
(2) 训练集和测试集的类标不同,通过全局变量动态增加新类标,对未知类型的检测是评价算法的重要指标。
#coding:utf-8
import numpy as np
import pandas as pd
import csv
“”"
功能:数据预处理 将KDD99数据集中字符型转换为数值型
原文:https://blog.csdn.net/asialee_bird/article/details/80491256
强烈推荐博友们阅读asialee_bird大神的文章及Github代码,非常厉害的一位博主。
修订:Eastmount 2019-11-22
“”"
#label_list为全局变量
global label_list
#文件名
source_file=‘kddcup.data_10_percent_corrected’
handled_file=‘kddcup.data_10_percent_corrected.csv’
#文件写入操作
data_file = open(handled_file,‘w’)
#将相应的非数字类型转换为数字标识即符号型数据转化为数值型数据
def find_index(x,y):
return [i for i in range(len(y)) if y[i]==x]
#定义将源文件行中3种协议类型转换成数字标识的函数
def handleProtocol(inputs):
protocol_list=[‘tcp’,‘udp’,‘icmp’]
if inputs[1] in protocol_list:
return find_index(inputs[1], protocol_list)[0]
#定义将源文件行中70种网络服务类型转换成数字标识的函数
def handleService(inputs):
service_list=[‘aol’,‘auth’,‘bgp’,‘courier’,‘csnet_ns’,‘ctf’,‘daytime’,‘discard’,‘domain’,‘domain_u’,
‘echo’,‘eco_i’,‘ecr_i’,‘efs’,‘exec’,‘finger’,‘ftp’,‘ftp_data’,‘gopher’,‘harvest’,‘hostnames’,
‘http’,‘http_2784’,‘http_443’,‘http_8001’,‘imap4’,‘IRC’,‘iso_tsap’,‘klogin’,‘kshell’,‘ldap’,
‘link’,‘login’,‘mtp’,‘name’,‘netbios_dgm’,‘netbios_ns’,‘netbios_ssn’,‘netstat’,‘nnsp’,‘nntp’,
‘ntp_u’,‘other’,‘pm_dump’,‘pop_2’,‘pop_3’,‘printer’,‘private’,‘red_i’,‘remote_job’,‘rje’,‘shell’,
‘smtp’,‘sql_net’,‘ssh’,‘sunrpc’,‘supdup’,‘systat’,‘telnet’,‘tftp_u’,‘tim_i’,‘time’,‘urh_i’,‘urp_i’,
‘uucp’,‘uucp_path’,‘vmnet’,‘whois’,‘X11’,‘Z39_50’]
if inputs[2] in service_list:
return find_index(inputs[2],service_list)[0]
#定义将源文件行中11种网络连接状态转换成数字标识的函数
def handleFlag(inputs):
flag_list=[‘OTH’,‘REJ’,‘RSTO’,‘RSTOS0’,‘RSTR’,‘S0’,‘S1’,‘S2’,‘S3’,‘SF’,‘SH’]
if inputs[3] in flag_list:
return find_index(inputs[3],flag_list)[0]
#定义将源文件行中攻击类型转换成数字标识的函数(训练集中共出现了22个攻击类型,而剩下的17种只在测试集中出现)
def handleLabel(inputs):
label_list=[‘normal.’, ‘buffer_overflow.’, ‘loadmodule.’, ‘perl.’, ‘neptune.’, ‘smurf.’,
‘guess_passwd.’, ‘pod.’, ‘teardrop.’, ‘portsweep.’, ‘ipsweep.’, ‘land.’, ‘ftp_write.’,
‘back.’, ‘imap.’, ‘satan.’, ‘phf.’, ‘nmap.’, ‘multihop.’, ‘warezmaster.’, ‘warezclient.’,
‘spy.’, ‘rootkit.’]
#在函数内部使用全局变量并修改它
global label_list
if inputs[41] in label_list:
return find_index(inputs[41],label_list)[0]
else:
label_list.append(inputs[41])
return find_index(inputs[41],label_list)[0]
#主函数
if name==‘main’:
#循环读取文件数据
with open(source_file,‘r’) as data_source:
csv_reader = csv.reader(data_source)
csv_writer = csv.writer(data_file)
count = 0 #行数
for row in csv_reader:
temp_line=np.array(row)
temp_line[1] = handleProtocol(row) #将源文件行中3种协议类型转换成数字标识
temp_line[2] = handleService(row) #将源文件行中70种网络服务类型转换成数字标识
temp_line[3] = handleFlag(row) #将源文件行中11种网络连接状态转换成数字标识
temp_line[41] = handleLabel(row) #将源文件行中23种攻击类型转换成数字标识
csv_writer.writerow(temp_line)
count += 1
#输出每行数据中所修改后的状态
#print(count,'status:',temp_line[1],temp_line[2],temp_line[3],temp_line[41])
data_file.close()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
处理后的结果如下图所示:
0,2,12,9,520,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,457,457,0.00,0.00,0.00,0.00,1.00,0.00,0.00,255,255,1.00,0.00,1.00,0.00,0.00,0.00,0.00,0.00,5
0,0,21,9,428,7512,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,7,18,0.00,0.00,0.00,0.00,1.00,0.00,0.11,255,255,1.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0
四.KNN实现入侵检测
这里通过KNN算法实现一个最简单的入侵检测。
1.KNN
K最近邻(K-Nearest Neighbor,简称KNN)分类算法是数据挖掘分类技术中最简单常用的方法之一。所谓K最近邻,就是寻找K个最近的邻居的意思,每个样本都可以用它最接近的K个邻居来代表。本小节主要讲解KNN分类算法的基础知识及分析实例。
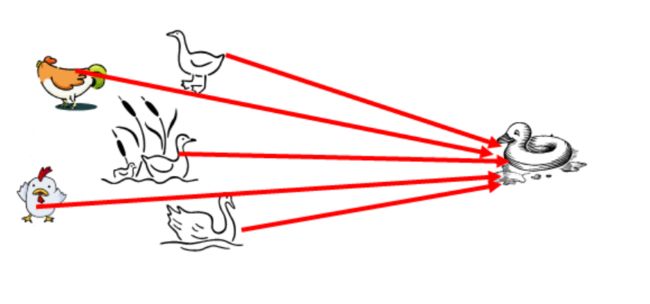
KNN分类算法是最近邻算法,字面意思就是寻找最近邻居,由Cover和Hart在1968年提出,简单直观易于实现。下面通过一个经典的例子来讲解如何寻找邻居,选取多少个邻居。下图是非常经典的KNN案例,需要判断右边这个动物是鸭子、鸡还是鹅?它涉及到了KNN算法的核心思想,判断与这个样本点相似的类别,再预测其所属类别。由于它走路和叫声像一只鸭子,所以右边的动物很可能是一只鸭子。
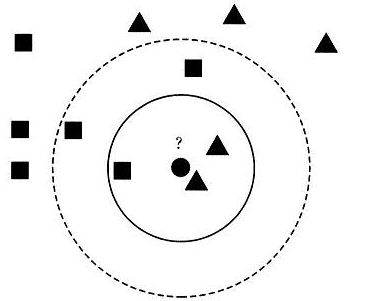
所以,KNN分类算法的核心思想是从训练样本中寻找所有训练样本X中与测试样本距离(欧氏距离)最近的前K个样本(作为相似度),再选择与待分类样本距离最小的K个样本作为X的K个最邻近,并检测这K个样本大部分属于哪一类样本,则认为这个测试样本类别属于这一类样本。假设现在需要判断下图中的圆形图案属于三角形还是正方形类别,采用KNN算法分析如下:
1.当K=3时,图中第一个圈包含了三个图形,其中三角形2个,正方形一个,该圆的则分类结果为三角形。
2.当K=5时,第二个圈中包含了5个图形,三角形2个,正方形3个,则以3:2的投票结果预测圆为正方形类标。
总之,设置不同的K值,可能预测得到不同的结果。
KNeighborsClassifier可以设置3种算法:brute、kd_tree、ball_tree,设置K值参数为n_neighbors=3。
调用方法如下:
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=3, algorithm=“ball_tree”)
它也包括两个方法:
- 训练:nbrs.fit(data, target)
- 预测:pre = clf.predict(data)
2.算法实现
接下来开始进行KNN算法分类分析,其中KNN核心算法主要步骤包括五步:
- 加载数据集
- 划分数据集
- KNN训练
- 评价算法
- 降维可视化
# -*- coding: utf-8 -*-
import os
import csv
import numpy as np
import pandas as pd
from sklearn import metrics
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
from sklearn import neighbors
#-----------------------------------------第一步 加载数据集-----------------------------------------
fr= open(“kddcup.data_10_percent_corrected.csv”)
lines = fr.readlines()
line_nums = len(lines)
print(line_nums)
#创建line_nums行 para_num列的矩阵
x_mat = np.zeros((line_nums, 41))
y_label = []
#划分数据集
for i in range(line_nums):
line = lines[i].strip()
item_mat = line.split(’,’)
x_mat[i, :] = item_mat[0:41] #前41个特征
y_label.append(item_mat[-1]) #类标
fr.close()
print x_mat.shape
print len(y_label)
#-----------------------------------------第二步 划分数据集-----------------------------------------
y = []
for n in y_label:
y.append(int(n))
y = np.array(y, dtype = int) #list转换数组
#划分数据集 测试集40%
train_data, test_data, train_target, test_target = train_test_split(x_mat, y, test_size=0.4, random_state=42)
print train_data.shape, train_target.shape
print test_data.shape, test_target.shape
#-----------------------------------------第三步 KNN训练-----------------------------------------
clf = neighbors.KNeighborsClassifier()
clf.fit(train_data, train_target)
print clf
result = clf.predict(test_data)
print result
print test_target
#-----------------------------------------第四步 评价算法-----------------------------------------
print sum(result==test_target) #预测结果与真实结果比对
print(metrics.classification_report(test_target, result)) #准确率 召回率 F值
#----------------------------------------第五步 降维可视化---------------------------------------
pca = PCA(n_components=2)
newData = pca.fit_transform(test_data)
plt.figure()
plt.scatter(newData[:,0], newData[:,1], c=test_target, s=50)
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
上面代码非常简单,其输出结果如下图所示。但也存在几个缺点:
- 数据集 kddcup.data_10_percent_corrected.csv 随机划分为训练集和测试集,而真实的是用某个数据集训练,另一个数据集预测,并且测试集中存在未知的攻击。
- 该代码没有考虑数据归一化、数据标准化处理,而该数据集数值集中分布几个值,这会影响最终实验结果。
- 该实验的评价应该计算ROC、AUC曲线,推荐这篇文章:机器学习分类算法常用评价指标
494021 (494021L, 41L) 494021 (296412L, 41L) (296412L,) (197609L, 41L) (197609L,) KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=None, n_neighbors=5, p=2, weights='uniform') [5 5 5 ... 5 4 5] [5 5 5 ... 5 4 5] 197299precision recall f1-score support 0 1.00 1.00 1.00 38977 1 0.88 0.50 0.64 14 2 0.00 0.00 0.00 2 3 0.00 0.00 0.00 2 4 1.00 1.00 1.00 42797 5 1.00 1.00 1.00 112364 6 0.92 0.96 0.94 23 7 0.94 1.00 0.97 93 8 0.98 1.00 0.99 398 9 0.94 0.87 0.91 434 10 0.91 0.97 0.94 497 11 1.00 0.75 0.86 8 12 0.00 0.00 0.00 2 13 1.00 0.99 1.00 879 14 1.00 0.50 0.67 4 15 0.98 0.89 0.93 602 16 1.00 1.00 1.00 1 17 0.75 0.49 0.60 85 18 0.00 0.00 0.00 2 19 0.86 0.86 0.86 7 20 0.96 0.98 0.97 415 22 0.00 0.00 0.00 3
micro avg 1.00 1.00 1.00 197609
macro avg 0.73 0.67 0.69 197609
weighted avg 1.00 1.00 1.00 197609
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
数据高度重叠,所以接下来我们对KNN算法进行优化。
五.入侵检测算法优化
1.数值标准化
数据标准化是机器学习、数据挖掘中常用的一种方法。
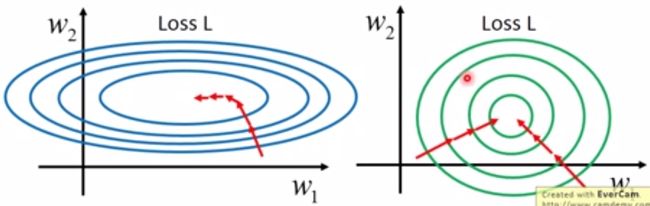
数据标准化主要是应对特征向量中数据很分散的情况,防止小数据被大数据(绝对值)吞并的情况。另外,数据标准化也有加速训练,防止梯度爆炸的作用。下面是从李宏毅教授视频中截下来的两张图,左图表示未经过数据标准化处理的loss更新函数,右图表示经过数据标准化后的loss更新图。可见经过标准化后的数据更容易迭代到最优点,而且收敛更快。
在聚类\分类算法中,使用计算距离的方法对数据进行聚类\分类,而连接记录的固定特征属性中有两种类型的数值——离散型和连续型。对于连续型特征属性,各属性的度量方法不一样。一般而言,所用的度量单位越小,变量可能的值域就越大,这样对聚类结果的影响也越大,即在计算数据间距离时对聚类的影响越大,甚至会出现“大数”吃“小数”的现象。
因此为了避免对度量单位选择的依赖,消除由于属性度量的差异对聚类\分类产生的影响,需要对属性值进行标准化。对于离散型特征属性本文中并不作标准化处理,而是放在聚类算法中计算距离时处理。所以数据标准化是针对连续型特征属性的。
设训练数据集有n条网络连接记录,每个记录中有22个连续型属性向量记作 Xij(1≤i≤n,11≤j≤41) 。对 Xij 数据预处理分为两步:数值标准化和数值归一化。
Z-score标准化:
基于数据均值和方差的标准化化方法。标准化后的数据是均值为0,方差为1的正态分布。这种方法要求原始数据的分布可以近似为高斯分布,否则效果会很差。标准化公式如下,
x ′ = x − m e a n s t d x ′ = x − m e a n s t d x ′ = x − m e a n s t d x′=x−meanstdx′=x−meanstd x' = \frac{x-mean}{std} x′=x−meanstdx′=x−meanstdx′=stdx−meanSTDi=n1(∣X1j−AVGj∣+∣X2j−AVGj∣+...+∣Xnj−AVGj∣)
其中,AVG为平均值,STAD为平均绝对偏差,如果AVG等于0,则X’=0;如果STD等于0,则X’=0。
核心代码如下所示,这里建议读者直接使用我的数据集或测试数据集测试,否则花费巨大时间。
#coding:utf-8
import numpy as np
import pandas as pd
import csv
#全局变量
global x_mat
#数据标准化
def ZscoreNormalization(x, n):
print(len(x))
i = 0
while i<len(x):
x_mat[i][n] = (x[i] - np.mean(x)) / np.std(x)
if x_mat[i][n]>0:
print(x_mat[i][n])
i = i + 1
print("The ", n , “feature is normal.”)
#-------------------------------------读取文件划分数据集-----------------------------------------
fr = open(“test-normal.csv”)
data_file = open(“test-normal-result.csv”,‘wb+’)
lines = fr.readlines()
line_nums = len(lines)
print(line_nums)
#创建line_nums行 para_num列的矩阵
x_mat = np.zeros((line_nums, 42))
#划分数据集
for i in range(line_nums):
line = lines[i].strip()
item_mat = line.split(’,’)
x_mat[i, :] = item_mat[0:42] #获取42个特征
fr.close()
print(x_mat.shape)
#--------------------------------获取某列特征并依次标准化并赋值-----------------------------
print(len(x_mat[:, 0])) #获取某列数据 494021
print(len(x_mat[0, :])) #获取某行数据 42
#标准化处理
ZscoreNormalization(x_mat[:, 0], 0) #duration
ZscoreNormalization(x_mat[:, 0], 4) #src_bytes
ZscoreNormalization(x_mat[:, 0], 5) #dst_bytes
ZscoreNormalization(x_mat[:, 0], 7) #wrong_fragment
ZscoreNormalization(x_mat[:, 0], 8) #urgent
ZscoreNormalization(x_mat[:, 0], 9) #hot
ZscoreNormalization(x_mat[:, 0], 10) #num_failed_logins
ZscoreNormalization(x_mat[:, 0], 12) #num_compromised
ZscoreNormalization(x_mat[:, 0], 14) #su_attempte
ZscoreNormalization(x_mat[:, 0], 15) #num_root
ZscoreNormalization(x_mat[:, 0], 16) #num_file_creations
ZscoreNormalization(x_mat[:, 0], 17) #num_shells
ZscoreNormalization(x_mat[:, 0], 18) #num_access_files
ZscoreNormalization(x_mat[:, 0], 19) #num_outbound_cmds
ZscoreNormalization(x_mat[:, 0], 22) #count
ZscoreNormalization(x_mat[:, 0], 23) #srv_count
ZscoreNormalization(x_mat[:, 0], 24) #serror_rate
ZscoreNormalization(x_mat[:, 0], 25) #srv_serror_rate
ZscoreNormalization(x_mat[:, 0], 26) #rerror_rate
ZscoreNormalization(x_mat[:, 0], 27) #srv_rerror_rate
ZscoreNormalization(x_mat[:, 0], 28) #same_srv_rate
ZscoreNormalization(x_mat[:, 0], 29) #diff_srv_rate
ZscoreNormalization(x_mat[:, 0], 30) #srv_diff_host_rate
ZscoreNormalization(x_mat[:, 0], 31) #dst_host_count
ZscoreNormalization(x_mat[:, 0], 32) #dst_host_srv_count
ZscoreNormalization(x_mat[:, 0], 33) #dst_host_same_srv_rate
ZscoreNormalization(x_mat[:, 0], 34) #dst_host_diff_srv_rate
ZscoreNormalization(x_mat[:, 0], 35) #dst_host_same_src_port_rate
ZscoreNormalization(x_mat[:, 0], 36) #dst_host_srv_diff_host_rate
ZscoreNormalization(x_mat[:, 0], 37) #dst_host_serror_rate
ZscoreNormalization(x_mat[:, 0], 38) #dst_host_srv_serror_rate
ZscoreNormalization(x_mat[:, 0], 39) #dst_host_rerror_rate
ZscoreNormalization(x_mat[:, 0], 40) #dst_host_srv_rerror_rate
#文件写入操作
csv_writer = csv.writer(data_file)
i = 0
while i<len(x_mat[:, 0]):
csv_writer.writerow(x_mat[i, :])
i = i + 1
data_file.close()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
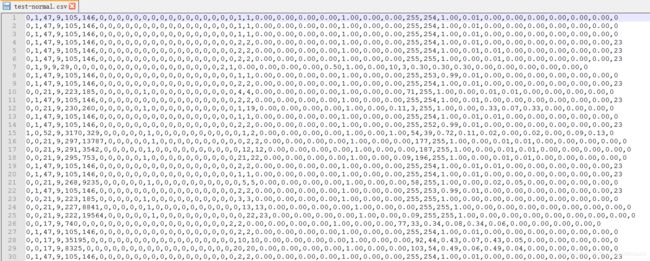
标准化之前的数据显示如下图所示:
0,1,47,9,105,146,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0.00,0.00,0.00,0.00,1.00,0.00,0.00,255,254,1.00,0.01,0.00,0.00,0.00,0.00,0.00,0.00,0
经常处理后的数据如下所示:
-0.024411893497851576,1.0,47.0,9.0,-0.030455897580918892,-0.030455897580918892,0.0,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,0.0,-0.030455897580918892,0.0,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,0.0,0.0,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,-0.030455897580918892,0
2.数值归一化
数据标准化(归一化)处理是数据挖掘的一项基础工作,不同评价指标往往具有不同的量纲和量纲单位,这样的情况会影响到数据分析的结果,为了消除指标之间的量纲影响,需要进行数据标准化处理,以解决数据指标之间的可比性。原始数据经过数据标准化处理后,各指标处于同一数量级,适合进行综合对比评价。以下是常用的归一化方法:
min-max标准化(Min-Max Normalization)
也称为离差标准化,是对原始数据的线性变换,使结果值映射到[0 , 1]之间。转换函数如下:
x ′ = x − m i n m a x − m i n x ′ = x − m i n m a x − m i n x ′ = x − m i n m a x − m i n x′=x−minmax−minx′=x−minmax−min x' = \frac{x-min}{max-min} x′=x−minmax−minx′=x−minmax−minx′=max−minx−minx′=max−minx−min
其中max为样本数据的最大值,min为样本数据的最小值。这种方法有个缺陷就是当有新数据加入时,可能导致max和min的变化,需要重新定义。min-max标准化python代码如下:
import numpy as np
arr = np.asarray([0, 10, 50, 80, 100])
for x in arr:
x = float(x - np.min(arr))/(np.max(arr)- np.min(arr))
print x
# output
# 0.0
# 0.1
# 0.5
# 0.8
# 1.0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
归一化核心代码如下所示:
#coding:utf-8
import numpy as np
import pandas as pd
import csv
#全局变量
global x_mat
#数据归一化
def MinmaxNormalization(x, n):
print(len(x))
i = 0
while i<len(x):
x_mat[i][n] = (x[i] - np.min(x)) / (np.max(x)-np.min(x))
#if x_mat[i][n]>0:
# print(x_mat[i][n])
i = i + 1
print("The ", n , “feature is normal.”)
#-------------------------------------读取文件划分数据集-----------------------------------------
fr = open(“test-normal-result.csv”)
data_file = open(“test-normal-result-minmax.csv”,‘wb+’)
lines = fr.readlines()
line_nums = len(lines)
print(line_nums)
#创建line_nums行 para_num列的矩阵
x_mat = np.zeros((line_nums, 42))
#划分数据集
for i in range(line_nums):
line = lines[i].strip()
item_mat = line.split(’,’)
x_mat[i, :] = item_mat[0:42] #获取42个特征
fr.close()
print(x_mat.shape)
#--------------------------------获取某列特征并依次标准化并赋值-----------------------------
print(len(x_mat[:, 0])) #获取某列数据 494021
print(len(x_mat[0, :])) #获取某行数据 42
#归一化处理
MinmaxNormalization(x_mat[:, 0], 0) #duration
MinmaxNormalization(x_mat[:, 0], 4) #src_bytes
MinmaxNormalization(x_mat[:, 0], 5) #dst_bytes
MinmaxNormalization(x_mat[:, 0], 7) #wrong_fragment
MinmaxNormalization(x_mat[:, 0], 8) #urgent
MinmaxNormalization(x_mat[:, 0], 9) #hot
MinmaxNormalization(x_mat[:, 0], 10) #num_failed_logins
MinmaxNormalization(x_mat[:, 0], 12) #num_compromised
MinmaxNormalization(x_mat[:, 0], 14) #su_attempte
MinmaxNormalization(x_mat[:, 0], 15) #num_root
MinmaxNormalization(x_mat[:, 0], 16) #num_file_creations
MinmaxNormalization(x_mat[:, 0], 17) #num_shells
MinmaxNormalization(x_mat[:, 0], 18) #num_access_files
MinmaxNormalization(x_mat[:, 0], 19) #num_outbound_cmds
MinmaxNormalization(x_mat[:, 0], 22) #count
MinmaxNormalization(x_mat[:, 0], 23) #srv_count
MinmaxNormalization(x_mat[:, 0], 24) #serror_rate
MinmaxNormalization(x_mat[:, 0], 25) #srv_serror_rate
MinmaxNormalization(x_mat[:, 0], 26) #rerror_rate
MinmaxNormalization(x_mat[:, 0], 27) #srv_rerror_rate
MinmaxNormalization(x_mat[:, 0], 28) #same_srv_rate
MinmaxNormalization(x_mat[:, 0], 29) #diff_srv_rate
MinmaxNormalization(x_mat[:, 0], 30) #srv_diff_host_rate
MinmaxNormalization(x_mat[:, 0], 31) #dst_host_count
MinmaxNormalization(x_mat[:, 0], 32) #dst_host_srv_count
MinmaxNormalization(x_mat[:, 0], 33) #dst_host_same_srv_rate
MinmaxNormalization(x_mat[:, 0], 34) #dst_host_diff_srv_rate
MinmaxNormalization(x_mat[:, 0], 35) #dst_host_same_src_port_rate
MinmaxNormalization(x_mat[:, 0], 36) #dst_host_srv_diff_host_rate
MinmaxNormalization(x_mat[:, 0], 37) #dst_host_serror_rate
MinmaxNormalization(x_mat[:, 0], 38) #dst_host_srv_serror_rate
MinmaxNormalization(x_mat[:, 0], 39) #dst_host_rerror_rate
MinmaxNormalization(x_mat[:, 0], 40) #dst_host_srv_rerror_rate
#文件写入操作
csv_writer = csv.writer(data_file)
i = 0
while i<len(x_mat[:, 0]):
csv_writer.writerow(x_mat[i, :])
i = i + 1
data_file.close()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
输出结果如下图所示:
5.1346198410647435e-05,1.0,47.0,9.0,5.1346198410647435e-05,5.1346198410647435e-05,0.0,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,0.0,5.1346198410647435e-05,0.0,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,0.0,0.0,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,5.1346198410647435e-05,0
3.KNN检测及评估
最后代码如下所示,主要包括以下功能:
- 针对上面标准化和归一化处理后的数据集,进行KNN算法分类
- 采用欧式距离计算,并绘制散点分布图(序列号、最小欧式距离、类标)
- ROC曲线评估
但实验效果非常不理想,不知道什么具体原因,哎,心累~博友们使用的时候帮忙检测下前面的标准化和归一化代码是否正确。
# -*- coding: utf-8 -*-
import os
import csv
import numpy as np
from sklearn.svm import SVC
from sklearn import metrics
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
from sklearn import neighbors
#-----------------------------------------第一步 加载数据集-----------------------------------------
fr= open(“kddcup.data_10_yxz-result-minmax.csv”)
lines = fr.readlines()
line_nums = len(lines)
print(line_nums)
#创建line_nums行 para_num列的矩阵
x_mat = np.zeros((line_nums, 31))
y_label = []
#划分数据集
for i in range(line_nums):
line = lines[i].strip()
item_mat = line.split(’,’)
x_mat[i, :] = item_mat[0:31] #前41个特征
y_label.append(item_mat[-1]) #类标
fr.close()
print(x_mat.shape)
print(len(y_label))
#-----------------------------------------第二步 划分数据集-----------------------------------------
y = []
for n in y_label:
y.append(int(float(n)))
y = np.array(y, dtype = int) #list转换数组
#划分数据集 测试集40%
train_data, test_data, train_target, test_target = train_test_split(x_mat, y, test_size=0.4, random_state=42)
print(train_data.shape, train_target.shape)
print(test_data.shape, test_target.shape)
#-----------------------------------------第三步 KNN训练-----------------------------------------
def classify(input_vct, data_set):
data_set_size = data_set.shape[0]
#扩充input_vct到与data_set同型并相减
diff_mat = np.tile(input_vct, (data_set_size, 1)) - data_set
sq_diff_mat = diff_mat2 #矩阵中每个元素都平方
distance = sq_diff_mat.sum(axis=1)0.5 #每行相加求和并开平方根
return distance.min(axis=0) #返回最小距离
test_size = len(test_target)
result = np.zeros((test_size, 3))
for i in range(test_size):
#序号 最小欧氏距离 测试集数据类别
result[i] = i + 1, classify(test_data[i], train_data), test_target[i]
#矩阵转置
result = np.transpose(result)
#-----------------------------------------第四步 评价及可视化-----------------------------------------
def roc(data_set):
normal = 0
data_set_size = data_set.shape[1]
roc_rate = np.zeros((2, data_set_size)) #输出ROC曲线 二维矩阵
#计算正常请求数量
for i in range(data_set_size):
if data_set[2][i] 1:
normal += 1
abnormal = data_set_size - normal
max_dis = data_set[1].max() #欧式距离最大值
for j in range(1000):
threshold = max_dis / 1000 * j
normal1 = 0
abnormal1 = 0
for k in range(data_set_size):
if data_set[1][k] > threshold and data_set[2][k] 1:
normal1 += 1
if data_set[1][k] > threshold and data_set[2][k] != 1:
abnormal1 += 1
roc_rate[0][j] = normal1 / normal # 阈值以上正常点/全体正常的点
roc_rate[1][j] = abnormal1 / abnormal # 阈值以上异常点/全体异常点
return roc_rate
#图1 散点图
#横轴为序号 纵轴为最小欧氏距离
#点中心颜色根据测试集数据类别而定 点外围无颜色 点大小为最小1 灰度为最大1
plt.figure(1)
plt.scatter(result[0], result[1], c=result[2], edgecolors=‘None’, s=2, alpha=1)
#图2 ROC曲线
#横轴误报率:即阈值以上正常点/全体正常的点
#纵轴检测率:即阈值以上异常点/全体异常点
roc_rate = roc(result)
plt.figure(2)
plt.scatter(roc_rate[0], roc_rate[1], edgecolors=‘None’, s=1, alpha=1)
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
4.Github代码分享
最后提供Github的代码,希望对读者有所帮助,参考龚炎大神的文章和代码。
https://blog.gongyan.me/2017/04/kdd-cup99/
https://github.com/gongyanc/kddcup99
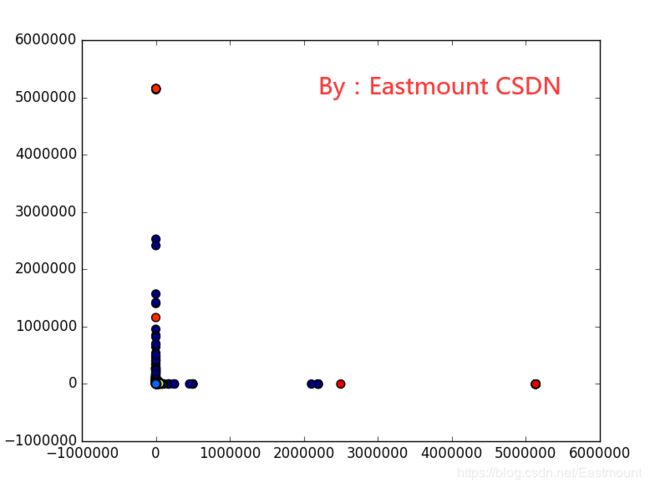
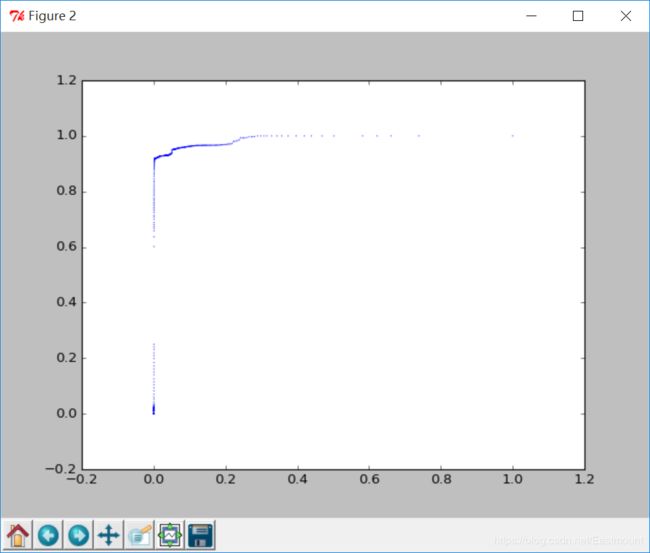
运行结果如下图所示,本篇文章所有资源参考我的Github。
横坐标序号,纵坐标最小欧式距离,散点颜色类标(正常、攻击)。
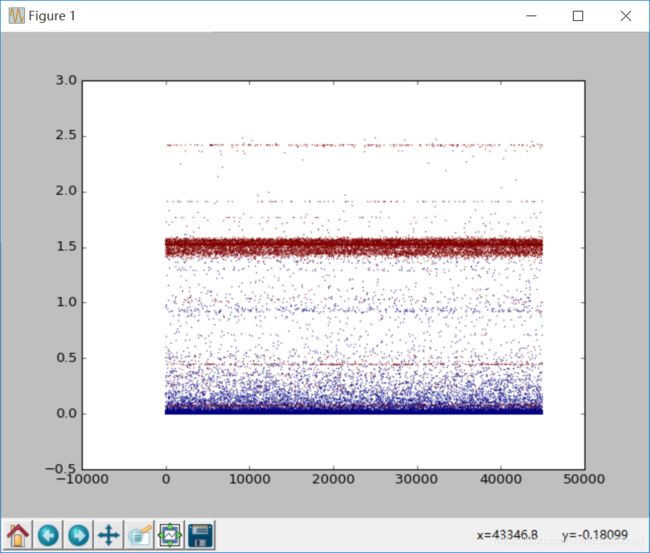
ROC曲线:
# coding=utf-8
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
def classify(input_vct, data_set):
data_set_size = data_set.shape[0]
diff_mat = np.tile(input_vct, (data_set_size, 1)) - data_set #扩充input_vct到与data_set同型并相减
sq_diff_mat = diff_mat2 #矩阵中每个元素都平方
distance = sq_diff_mat.sum(axis=1)0.5 #每行相加求和并开平方根
return distance.min(axis=0) #返回最小距离
def file2mat(test_filename, para_num):
“”"
将表格存入矩阵,test_filename为表格路径,para_num为存入矩阵的列数
返回目标矩阵,和矩阵每一行数据的类别
“”"
fr = open(test_filename)
lines = fr.readlines()
line_nums = len(lines)
result_mat = np.zeros((line_nums, para_num)) #创建line_nums行 para_num列的矩阵
class_label = []
for i in range(line_nums):
line = lines[i].strip()
item_mat = line.split(’,’)
result_mat[i, :] = item_mat[0: para_num]
class_label.append(item_mat[-1]) #表格中最后一列正常1异常2的分类存入class_label
fr.close()
return result_mat, class_label
def roc(data_set):
normal = 0
data_set_size = data_set.shape[1]
roc_rate = np.zeros((2, data_set_size))
for i in range(data_set_size):
if data_set[2][i] 1:
normal += 1
abnormal = data_set_size - normal
max_dis = data_set[1].max()
for j in range(1000):
threshold = max_dis / 1000 * j
normal1 = 0
abnormal1 = 0
for k in range(data_set_size):
if data_set[1][k] > threshold and data_set[2][k] 1:
normal1 += 1
if data_set[1][k] > threshold and data_set[2][k] == 2:
abnormal1 += 1
roc_rate[0][j] = normal1 / normal #阈值以上正常点/全体正常的点
roc_rate[1][j] = abnormal1 / abnormal #阈值以上异常点/全体异常点
return roc_rate
def test(training_filename, test_filename):
training_mat, training_label = file2mat(training_filename, 32)
test_mat, test_label = file2mat(test_filename, 32)
test_size = test_mat.shape[0]
result = np.zeros((test_size, 3))
for i in range(test_size):
result[i] = i + 1, classify(test_mat[i], training_mat), test_label[i] # 序号 最小欧氏距离 测试集数据类别
result = np.transpose(result) #矩阵转置
plt.figure(1)
plt.scatter(result[0], result[1], c=result[2], edgecolors=‘None’, s=1, alpha=1)
# 图1 散点图:横轴为序号,纵轴为最小欧氏距离,点中心颜色根据测试集数据类别而定, 点外围无颜色,点大小为最小1,灰度为最大1
roc_rate = roc(result)
plt.figure(2)
plt.scatter(roc_rate[0], roc_rate[1], edgecolors=‘None’, s=1, alpha=1)
# 图2 ROC曲线:横轴误报率,即阈值以上正常点/全体正常的点;纵轴检测率,即阈值以上异常点/全体异常点
plt.show()
if name == “main”:
test(‘training.csv’, ‘test.csv’)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
六.总结
写到这里,这篇基于机器学习的入侵检测和攻击识别分享完毕。严格意义上来说,这篇文章是数据分析,它有几个亮点:
(1) 详细介绍了数据分析预处理中字符特征转换为数值特征、数据标准化、数据归一化,这都是非常基础的工作。
(2) 结合入侵检测应用KNN实现分类。
(3) 绘制散点图采用序号、最小欧式距离、类标,ROC曲线绘制都是之前没分享的。
(4) 恶意代码或入侵检测,后续作者还会深入,包括源代码、二进制分析。
这篇文章中也有几个不足之处:
(1) 最后的实验效果非常不理想,但本文的整体思路是值得学习的,推荐各位从我的Github下载学习。
(2) 后续作者尝试结合深度学习、图像识别来进行恶意代码分析。
(3) 作者刚刚学习安全领域,还非常菜,还有太多要学习的知识,但会一直努力的。
总之,希望基础性文章对您有所帮助,如果文章中有错误或不足之处,还请提出和海涵,希望与您共同进步。
天行健,君子以自强不息。
地势坤,君子以厚德载物。
(By:Eastmount 2019-11-23 周末写于武大 早上11点 http://blog.csdn.net/eastmount/ )