【Code】关于 GCN,我有三种写法
本篇文章主要基于 DGL 框架用三种不同的方式来实现图卷积神经网络。
1. DGL
DGL(Deep Graph Library)框架是由纽约大学和 AWS 工程师共同开发的开源框架,旨在为大家提供一个在图上进行深度学习的工具,帮助大家更高效的实现算法。
用现有的一些框架比如 TensorFlow、Pytorch、MXNet 等实现图神经网络模型都不太方便,同样现有框架实现图神经网络模型的速度不够快。
DGL 框架设计理念主要在于将图神经网络看作是消息传递的过程,每一个节点会发出它自己的消息,也会接收来自其它节点的消息。然后在得到所有信息之后做聚合,计算出节点新的表示。原有的深度学习框架都是进行张量运算,但是图很多时候并不能直接表示成一个完整的张量,需要手动补零,这其实很麻烦,不高效。
DGL 是基于现有框架,帮助用户更容易实现图神经网络模型。DGL 现在主要是以消息传递的接口作为核心,同时提供图采样以及批量处理图的接口。
关于 DGL 就不再进行过多介绍,感兴趣的同学可以去官网(http://dgl.ai/)了解。
2. Prepare
import torch
import time
import math
import dgl
import numpy as np
import torch.nn as nn
from dgl.data import citation_graph as citegrh
from dgl import DGLGraph
import dgl.function as fn
import networkx as nx
import torch.nn.functional as F
# 疑问 1: 为什么可以直接从 pytorch 中导入 GraphConv,这个不应该是 conv 文件中的吗
from dgl.nn import GraphConv
# from dgl.nn.pytorch import GraphConv
# from dgl.nn.pytorch.conv import GraphConv
这里有三种导入方法,建议用第一种,因为 DGL 的开发同学设计了一个机制,会自动 detect 用了什么 beckend,从而适配对应的 backend 的 api。
print(torch.__version__)
print(dgl.__version__)
print(nx.__version__)
1.4.0
0.4.3
2.3
3. GCN
3.1 First version
DGL 的第一种写法是利用 DGL 预定义的图卷积模块 GraphConv 来实现的。
GCN 的数学公式如下:
h i ( l + 1 ) = σ ( b ( l ) + ∑ j ∈ N ( i ) 1 c i j h j ( l ) W ( l ) ) h_i^{(l+1)} = \sigma(b^{(l)} + \sum_{j\in\mathcal{N}(i)}\frac{1}{c_{ij}}h_j^{(l)}W^{(l)}) hi(l+1)=σ(b(l)+j∈N(i)∑cij1hj(l)W(l))
其中, N ( i ) \mathcal{N}(i) N(i) 为节点的邻居集合, c i j = ∣ N ( i ) ∣ ∣ N ( j ) ∣ c_{ij}=\sqrt{|\mathcal{N}(i)|}\sqrt{|\mathcal{N}(j)|} cij=∣N(i)∣∣N(j)∣ 表示节点度的平方根的乘积,用于归一化数据, s i g m a sigma sigma 为激活函数
GraphConv 模型参数初始化参考 tkipf 大佬的原始实现,其中 W ( l ) W^{(l)} W(l) 使用 Glorot uniform 统一初始化,并将偏差初始化为零。
简单介绍下 Glorot 均匀分布(uniform)
Glorot 均匀分布,也叫 Xavier 均匀分布,该方法源于 2010 年的一篇论文《Understanding the difficulty of training deep feedforward neural networks》。其核心思想在于:为了使得网络中信息更好的流动,每一层输出的方差应该尽量相等。基于这个目标,权重 W 的方差需要满足 ∀ i V a r [ W i ] = 2 n i + n i + 1 \forall i \; Var[W^i] = \frac{2}{n_{i}+n_{i+1}} ∀iVar[Wi]=ni+ni+12,我们知道均匀分布的方差为: V a r = ( b − a ) 2 12 Var=\frac{(b-a)^2}{12} Var=12(b−a)2。所以我们可以初始化 W 为 Xavier 均匀分布: W ∼ U [ − 6 n j + n j + 1 , 6 n j + n j + 1 ] W \sim U[-\frac{\sqrt{6}}{\sqrt{n_j+n_{j+1}}}, \frac{\sqrt{6}}{\sqrt{n_j+n_{j+1}}}] W∼U[−nj+nj+16,nj+nj+16] (具体证明见论文)
class GCN(nn.Module):
def __init__(self,
g,
in_feats,
n_hidden,
n_classes,
n_layers,
activation,
dropout):
super(GCN, self).__init__()
self.g = g
self.layers = nn.ModuleList()
# input layer
self.layers.append(GraphConv(in_feats, n_hidden, activation=activation))
# output layer
for i in range(n_layers - 1):
self.layers.append(GraphConv(n_hidden, n_hidden, activation=activation))
# output layer
self.layers.append(GraphConv(n_hidden, n_classes))
self.dropout = nn.Dropout(p=dropout)
def forward(self, features):
h = features
for i, layers in enumerate(self.layers):
if i!=0:
h = self.dropout(h)
h = layers(self.g, h)
return h
3.2 Second version
3.2.1 ndata
DGL 的第二种写法:使用用户自定义的 Message 和 Reduce 函数
ndata 是 DGL 的一个特殊的语法,可以用于赋值(获得)某些节点的特征:
x = tourch.randn(10, 3)
g.ndata['x'] = x
如果指定某些节点的特征,可以进行切片操作:
g.ndata['x'][0] = th.zeros(1, 3)
g.ndata['x'][[0, 1, 2]] = th.zeros(3, 3)
g.ndata['x'][th.tensor([0, 1, 2])] = th.randn((3, 3))
当然也可以获得边的特征:
g.edata['w'] = th.randn(9, 2)
# Access edge set with IDs in integer, list, or integer tensor
g.edata['w'][1] = th.randn(1, 2)
g.edata['w'][[0, 1, 2]] = th.zeros(3, 2)
g.edata['w'][th.tensor([0, 1, 2])] = th.zeros(3, 2)
# You can get the edge ids by giving endpoints, which are useful for accessing the features.
g.edata['w'][g.edge_id(1, 0)] = th.ones(1, 2) # edge 1 -> 0
g.edata['w'][g.edge_ids([1, 2, 3], [0, 0, 0])] = th.ones(3, 2) # edges [1, 2, 3] -> 0
# Use edge broadcasting whenever applicable.
g.edata['w'][g.edge_ids([1, 2, 3], 0)] = th.ones(3, 2) # edges [1, 2, 3] -> 0
3.2.2 UDFs
在 DGL 中,通过用户自定义的函数(User-defined functions,UDFs)来实现消息传递和节点特征变换。
可以利用 Edge UDFs 来定义一个消息(Message)函数,其功能在于基于边传递消息。具体实现如下:
def gcn_msg(edge):
msg = edge.src['h'] * edge.src['norm']
return {'m': msg}
Edge UDFs 需要传入一个 edge 参数,其中 edge 有三个属性:src、dst、data,分别对应源节点特征、目标节点特征和边特征。
我们的 Message 函数,是从源节点向目标节点传递,所以只考虑源节点的特征。
节点中的 ‘norm’ 用于归一化,具体计算方式后面会说。
对于每个节点来说,可能过会收到很多个源节点传过来的消息,所以可以将这些消息存储在邮箱中(mailbox)。
我们那再来定义一个聚合(Reduce)函数。
消息传递完后,每个节点都要处理下他们的“信箱”(mailbox),Reduce 函数的作用就是用来处理节点“信箱”的消息的。
Reduce 函数是一个 Node UDFs。
Node UDFs 接收一个 node 的参数,并且 node 有两个属性 data 和 mailbox,分别为节点的特征和用来接收信息的“信箱”。
def gcn_reduce(node):
# 需要注意:消息存放在 mailbox 的第二个维上,第一维是消息的数量
accum = torch.sum(node.mailbox['m'], dim=1) * node.data['norm']
return {'h': accum}
Messge UDF 作用于边上,而 Reduce UDF 作用于节点上。两者的关系如下:
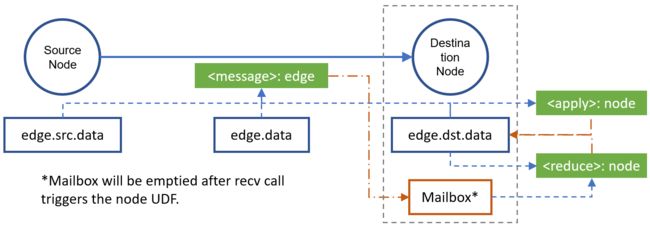
从左到右开始看,源节点通过 message 函数传递节点特征,并传递到目标节点的 Mailbox 中,在触发 Node UDF 时(这里为 Reduce 函数),Mailbox 将被清空。
上图中我们还可以看到作用于节点的有两个函数:Apply 函数和 Reduce 函数。
Reduce 函数我们上面介绍过了,那这个 Apply 函数是什么呢?
Apply 函数为节点更新的函数,可以用于初始化参数和对节点特征的进行非线形变换。
初始化参数:我们刚刚指出,参数分布服从 Glorot 均匀分布,所以要给节点加偏置的话,我们也需要将其初始化为并使其服从 Glorot 均匀分布,如下面代码中的 reset_parameters 函数
非线形变换:GCN 中每一层进行传递后,节点可能需要进行非线形变换,如下面代码中 forward 函数
class NodeApplyModule(nn.Module):
def __init__(self, out_feats, activation=None, bias=True):
super(NodeApplyModule, self).__init__()
if bias:
self.bias = nn.Parameter(torch.Tensor(out_feats))
else:
self.bias = None
self.activation = activation
self.reset_parameters()
def reset_parameters(self):
if self.bias is not None:
stdv = 1. / math.sqrt(self.bias.size(0))
self.bias.data.uniform_(-stdv, stdv)
def forward(self, nodes):
h = nodes.data['h']
if self.bias is not None:
h = h + self.bias
if self.activation:
h = self.activation(h)
return {'h': h}
有了 Message 函数、Reduce 函数和节点的更新函数后,我们需要将其连贯起来:
g.update_all(message_func='default',
reduce_func='default',
apply_node_func='default')
这个函数可以用于发送信息并更新所有节点,是 send() 和 recv() 函数的一个简单组合
3.2.3 GCNLayer
有了这些后,我们便可以定义 GCNLayer 了:
class GCNLayer(nn.Module):
def __init__(self,
g,
in_feats,
out_feats,
activation,
dropout,
bias=True):
super(GCNLayer, self).__init__()
self.g = g
self.weight = nn.Parameter(torch.Tensor(in_feats, out_feats))
if dropout:
self.dropout = nn.Dropout(p=dropout)
else:
self.dropout = 0.
self.node_update = NodeApplyModule(out_feats, activation, bias)
self.reset_parameters()
def reset_parameters(self):
stdv = 1. / math.sqrt(self.weight.size(1))
self.weight.data.uniform_(-stdv, stdv)
def forward(self, h):
if self.dropout:
h = self.dropout(h)
self.g.ndata['h'] = torch.mm(h, self.weight)
self.g.update_all(gcn_msg, gcn_reduce, self.node_update)
h = self.g.ndata.pop('h')
return h
然后我们把 GCNLayer 拼接在一起组成 GCN 网络
class GCN(nn.Module):
def __init__(self,
g,
in_feats,
n_hidden,
n_classes,
n_layers,
activation,
dropout):
super(GCN, self).__init__()
self.layers = nn.ModuleList()
# input layer
self.layers.append(GCNLayer(g, in_feats, n_hidden, activation, dropout))
# hidden layers
for i in range(n_layers - 1):
self.layers.append(GCNLayer(g, n_hidden, n_hidden, activation, dropout))
# output layer
self.layers.append(GCNLayer(g, n_hidden, n_classes, None, dropout))
def forward(self, features):
h = features
for layer in self.layers:
h = layer(h)
return h
3.3 Third version
DGL 的第三种写法:使用 DGL 的内置(builtin)函数
由于 Messge 和 Reduce 函数使用的比较频繁,所以 DGL 了内置函数以方便使用,我们把刚刚的 Message 和 Reduce 函数改变为内置函数有:
-
dgl.function.copy_src(src, out):Message 函数其实就是把源节点的特征拷贝到目标节点,所以可以换用内置的 copy_src 函数。
-
dgl.function.sum(msg, out):Reduce 函数其实就是聚合节点 Mailbox 中的消息,所以可以换用内置的 sum 函数。
class GCNLayer(nn.Module):
def __init__(self,
g,
in_feats,
out_feats,
activation,
dropout,
bias=True):
super(GCNLayer, self).__init__()
self.g = g
self.weight = nn.Parameter(torch.Tensor(in_feats, out_feats))
if bias:
self.bias = nn.Parameter(torch.Tensor(out_feats))
else:
self.bias = None
self.activation = activation
if dropout:
self.dropout = nn.Dropout(p=dropout)
else:
self.dropout = 0.
self.reset_parameters()
def reset_parameters(self):
stdv = 1. / math.sqrt(self.weight.size(1))
self.weight.data.uniform_(-stdv, stdv)
if self.bias is not None:
self.bias.data.uniform_(-stdv, stdv)
def forward(self, h):
if self.dropout:
h = self.dropout(h)
h = torch.mm(h, self.weight)
# normalization by square root of src degree
h = h * self.g.ndata['norm']
self.g.ndata['h'] = h
self.g.update_all(fn.copy_src(src='h', out='m'),
fn.sum(msg='m', out='h'))
h = self.g.ndata.pop('h')
# normalization by square root of dst degree
h = h * self.g.ndata['norm']
# bias
if self.bias is not None:
h = h + self.bias
if self.activation:
h = self.activation(h)
return h
- 这里的做了两次的标准化,对应 GCN 公式中的 c i j = ∣ N ( i ) ∣ ∣ N ( j ) ∣ c_{ij}=\sqrt{|\mathcal{N}(i)|}\sqrt{|\mathcal{N}(j)|} cij=∣N(i)∣∣N(j)∣;
- 这里把 Node 的 Apply 函数的功能合并到 GCNLayer 中了。
class GCN(nn.Module):
def __init__(self,
g,
in_feats,
n_hidden,
n_classes,
n_layers,
activation,
dropout):
super(GCN, self).__init__()
self.layers = nn.ModuleList()
# input layer
self.layers.append(GCNLayer(g, in_feats, n_hidden, activation, 0.))
# hidden layers
for i in range(n_layers - 1):
self.layers.append(GCNLayer(g, n_hidden, n_hidden, activation, dropout))
# output layer
self.layers.append(GCNLayer(g, n_hidden, n_classes, None, dropout))
def forward(self, features):
h = features
for layer in self.layers:
h = layer(h)
return h
4.Train
dropout=0.5
gpu=-1
lr=0.01
n_epochs=200
n_hidden=16 # 隐藏层节点的数量
n_layers=2 # 输入层 + 输出层的数量
weight_decay=5e-4 # 权重衰减
self_loop=True # 自循环
# cora 数据集
data = citegrh.load_cora()
features = torch.FloatTensor(data.features)
labels = torch.LongTensor(data.labels)
train_mask = torch.BoolTensor(data.train_mask)
val_mask = torch.BoolTensor(data.val_mask)
test_mask = torch.BoolTensor(data.test_mask)
in_feats = features.shape[1]
n_classes = data.num_labels
n_edges = data.graph.number_of_edges()
# 构建 DGLGraph
g = data.graph
if self_loop:
g.remove_edges_from(nx.selfloop_edges(g))
g.add_edges_from(zip(g.nodes(), g.nodes()))
g = DGLGraph(g)
这里大家可能会有些疑惑:为什么要先移除自环?然后再加上自环。
这个主要是为了防止原本数据集中有一部分的自环,如果不去掉直接加上自环的话,会导致一些节点有两个自环,而有些只有一个。
# 加载 GPU
if gpu < 0:
cuda = False
else:
cuda = True
torch.cuda.set_device(gpu)
features = features.cuda()
labels = labels.cuda()
train_mask = train_mask.cuda()
val_mask = val_mask.cuda()
test_mask = test_mask.cuda()
# 归一化,依据入度进行计算
degs = g.in_degrees().float()
norm = torch.pow(degs, -0.5)
norm[torch.isinf(norm)] = 0
if cuda:
norm = norm.cuda()
g.ndata['norm'] = norm.unsqueeze(1)
# 创建一个 GCN 的模型,可以选择上面的任意一个进行初始化
model = GCN(g,
in_feats,
n_hidden,
n_classes,
n_layers,
F.relu,
dropout)
if cuda:
model.cuda()
# 采用交叉熵损失函数和 Adam 优化器
loss_fcn = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(),
lr=lr,
weight_decay=weight_decay)
# 定义一个评估函数
def evaluate(model, features, labels, mask):
model.eval()
with torch.no_grad():
logits = model(features)
logits = logits[mask]
labels = labels[mask]
_, indices = torch.max(logits, dim=1)
correct = torch.sum(indices == labels)
return correct.item() * 1.0 / len(labels)
# 训练,并评估
dur = []
for epoch in range(n_epochs):
model.train()
t0 = time.time()
# forward
logits = model(features)
loss = loss_fcn(logits[train_mask], labels[train_mask])
optimizer.zero_grad()
loss.backward()
optimizer.step()
dur.append(time.time() - t0)
if epoch % 10 == 0:
acc = evaluate(model, features, labels, val_mask)
print("Epoch {:05d} | Time(s) {:.4f} | Loss {:.4f} | Accuracy {:.4f} | "
"ETputs(KTEPS) {:.2f}". format(epoch, np.mean(dur), loss.item(),
acc, n_edges / np.mean(dur) / 1000))
print()
acc = evaluate(model, features, labels, test_mask)
print("Test accuracy {:.2%}".format(acc))
Epoch 00000 | Time(s) 0.0178 | Loss 1.9446 | Accuracy 0.2100 | ETputs(KTEPS) 594.54
Epoch 00010 | Time(s) 0.0153 | Loss 1.7609 | Accuracy 0.3533 | ETputs(KTEPS) 689.33
Epoch 00020 | Time(s) 0.0150 | Loss 1.5518 | Accuracy 0.5633 | ETputs(KTEPS) 703.47
Epoch 00030 | Time(s) 0.0146 | Loss 1.2769 | Accuracy 0.5867 | ETputs(KTEPS) 721.28
Epoch 00040 | Time(s) 0.0143 | Loss 1.0785 | Accuracy 0.6567 | ETputs(KTEPS) 740.36
Epoch 00050 | Time(s) 0.0140 | Loss 0.8881 | Accuracy 0.7067 | ETputs(KTEPS) 754.21
Epoch 00060 | Time(s) 0.0138 | Loss 0.6994 | Accuracy 0.7533 | ETputs(KTEPS) 763.21
Epoch 00070 | Time(s) 0.0137 | Loss 0.6249 | Accuracy 0.7800 | ETputs(KTEPS) 770.54
Epoch 00080 | Time(s) 0.0137 | Loss 0.5048 | Accuracy 0.7800 | ETputs(KTEPS) 772.31
Epoch 00090 | Time(s) 0.0136 | Loss 0.4457 | Accuracy 0.7867 | ETputs(KTEPS) 778.78
Epoch 00100 | Time(s) 0.0135 | Loss 0.4167 | Accuracy 0.7800 | ETputs(KTEPS) 782.25
Epoch 00110 | Time(s) 0.0134 | Loss 0.3389 | Accuracy 0.8000 | ETputs(KTEPS) 786.52
Epoch 00120 | Time(s) 0.0134 | Loss 0.3777 | Accuracy 0.8100 | ETputs(KTEPS) 789.85
Epoch 00130 | Time(s) 0.0133 | Loss 0.3307 | Accuracy 0.8133 | ETputs(KTEPS) 792.00
Epoch 00140 | Time(s) 0.0133 | Loss 0.2542 | Accuracy 0.7933 | ETputs(KTEPS) 794.13
Epoch 00150 | Time(s) 0.0133 | Loss 0.2937 | Accuracy 0.8000 | ETputs(KTEPS) 795.73
Epoch 00160 | Time(s) 0.0132 | Loss 0.2944 | Accuracy 0.8333 | ETputs(KTEPS) 797.04
Epoch 00170 | Time(s) 0.0132 | Loss 0.2161 | Accuracy 0.8167 | ETputs(KTEPS) 799.74
Epoch 00180 | Time(s) 0.0132 | Loss 0.1972 | Accuracy 0.8200 | ETputs(KTEPS) 801.31
Epoch 00190 | Time(s) 0.0131 | Loss 0.2339 | Accuracy 0.8167 | ETputs(KTEPS) 802.92
Test accuracy 80.40%
5.Conclusion
以上便是本教程的全部,当然还有其他实现的方法,比如说,直接利用矩阵相乘来进行迭代。
6.Reference
- DGL Github
- DGL 官方文档
- 《深度学习——Xavier初始化方法》
- 《DGL 作者答疑!关于 DGL 你想知道的都在这里-周金晶》
关注公众号跟踪最新内容:阿泽的学习笔记。
