无损压缩算法专题——RLE算法实现
一、前言
本文是基于我的另一篇博客《无损压缩算法专题——无损压缩算法介绍》的基础上来实现的,RLE算法最简单的理解就是用(重复数,数据值)这样一个标记来代替待压缩数据中的连续重复的数据,以此来达到数据压缩的目的。说是这么说,但是具体实现起来有好几种方案,接下来一一介绍RLE(游程编码)的基本实现以及对该算法的改进。
二、PCX图像文件的RLE压缩方式
如果图像数据有连续相同的值,则用两个字节来代替这一串相同的字节,第一个字节的高两个bit设置为1做标志位,其余6个bit的值用来代表相同数据的个数,最多表示63;第二个字节用来代表这串相同数据的值。如果图像数据值不相同,分两种情况考虑:一种情况是数据值大于等于0xC0,则用两个字节表示,第一个字节为0xC1,第二个字节为该数据;第二种情况是数据值小于0xC0,则直接用一个字节输出该数据。下图是PCX文件中RLE压缩算法的数据结构图:
这幅图是我直接引用了一篇论文上的图,这篇论文在下文会继续提到。上面提到的这种压缩方式个人觉得不是非常的好,在对重复量非常少的数据进行该算法的话,很有可能使得压缩后的数据反而增大了,原因是对于不同的数据值而言,花费了大量的标记字节0xC1去区分它们。
三、 RLE算法改进——对连续数据和不连续数据段统一分段处理
这种方式其实是比较容易思考到的一个方向,我也是参考了网上的一片博客的,吃水不忘挖井人,这里我贴上链接表示感谢https://www.cnblogs.com/makai/p/11188968.html,浓缩一下讲述的内容,就是在遇到不重复的单个数据时,不是一个标记一个数据这样的输出方式,而是直接将这段区间内不连续的数据个数做一个统计,然后用一个标记表明接下来有多少个数据是不连续的,这种压缩方式只用一个标记字节就完成了对许多不重复字节的标记,相比较于PCX方式而言是很明显有优势的,节省了大量标记字节的开销。由于需要区分这个标记字节是标记的重复的数据还是不重复的数据,所以取字节的最高位来做标记,为0表示是不重复的数据,为1表示是重复的数据,剩下的7个bit用来表示数据的个数,所以最大可以标记127个字节,和PCX方式对比,不但节省了标记字节,还把标记数据的最大数目从63提升到了127。接下来是该算法的实现,代码中的注释已经标的不能再详细了。
Python实现如下:
import ctypes
class RLE():
def __init__(self):
self.threshold = 3 #启动压缩的阈值,大于这个阈值才有必要压缩
#文件压缩
def RLE_encode(self, readfilename, writefilename):
fread = open(readfilename, "rb") #以二进制方式读取文件
fwrite = open(writefilename, "wb") #以二进制方式写入文件
buf = b'' #前向缓冲区
bufSize = 127 + self.threshold #前向缓冲区大小
singleStore = b'' #无匹配的数据暂存区
sigleStoreSize = 127 #无匹配的数据长度,没有加上阈值是因为匹配数可能小于阈值
buf = fread.read(bufSize - len(buf)) #尽可能将buf填满
while len(buf) >= self.threshold: #大于3个字节才有必要压缩
curIndex = 0 #当前匹配位置
if (buf[curIndex] == buf[curIndex + 1]): #如果和下一个数据相同
if (buf[curIndex + 1] == buf[curIndex + 2]): #如果往后两个数据都是相同的,启动压缩
curIndex += 1
#不断向后寻找相同的数据
while ((curIndex + 2) < (len(buf))) and (buf[curIndex + 1] == buf[curIndex + 2]):
curIndex += 1
#相同的数据搜索完毕,如果之前有无匹配的数据没写入文件,先写入
if singleStore != b'':
fwrite.write(bytes(ctypes.c_uint8(len(singleStore)))) #写入 标记+匹配数
fwrite.write(singleStore) #写入所有无匹配的数据
singleStore = b'' #清空暂存区
fwrite.write(bytes(ctypes.c_uint8((1 << 7) + curIndex + 2 - self.threshold))) #写入 标记+匹配数
fwrite.write(bytes(ctypes.c_uint8(buf[0]))) #写入这个重复出现的数据
else:
singleStore += buf[curIndex: curIndex + 2] #将2个不能匹配的数据加入暂存区
buf = buf[curIndex + 2 : ] #从buf里清掉已经处理过的数据
else:
singleStore += buf[curIndex: curIndex + 1] #将1个不能匹配的数据加入暂存区
buf = buf[curIndex + 1:] #从buf里清掉已经处理过的数据
# 无匹配的数据存满了暂存区需要写入一次文件
if len(singleStore) >= sigleStoreSize:
fwrite.write(bytes(ctypes.c_uint8(sigleStoreSize))) # 写入 标记+匹配数
fwrite.write(singleStore[0:sigleStoreSize]) # 写入bufSize个无匹配的数据
singleStore = singleStore[sigleStoreSize:] # 从暂存区里清掉已经处理过的数据
buf += fread.read(bufSize - len(buf)) #尽可能将buf填满
singleStore += buf #将前向缓冲区里剩余的数据加入无匹配数据暂存区
if len(singleStore) >= sigleStoreSize:
fwrite.write(bytes(ctypes.c_uint8(sigleStoreSize))) # 写入 标记+匹配数
fwrite.write(singleStore[0:sigleStoreSize]) # 写入bufSize个无匹配的数据
singleStore = singleStore[sigleStoreSize:] # 从暂存区里清掉已经处理过的数据
if singleStore != b'':
fwrite.write(bytes(ctypes.c_uint8(len(singleStore))))
fwrite.write(singleStore)
fread.close()
fwrite.close()
#文件解压
def RLE_decode(self, readfilename, writefilename):
fread = open(readfilename, "rb") #以二进制方式读取文件
fwrite = open(writefilename, "wb") #以二进制方式写入文件
sign = fread.read(1) #读取标记字节
while sign != b'':
if sign[0] >= (1<<7): #如果是压缩标记
fwrite.write(fread.read(1) * (sign[0] - (1 << 7) + self.threshold)) #解压释放数据
else: #如果不是压缩标记
buf = fread.read(sign[0]) #读取无匹配的所有数据
fwrite.write(buf) #写入无匹配的数据
sign = fread.read(1) #读取下一个标记字节
fread.close()
fwrite.close()
if __name__ == '__main__':
Demo = RLE()
Demo.RLE_encode('5.bmp', 'test.encode')
Demo.RLE_decode('test.encode', 'test.decode')
在我具体实现的时候做了一小点的改动,加了个threshold阈值变量来扩充可标记的最大数目,因为对于连续的重复数据来说,如果只有两个字节重复,是没有必要压缩的,因为压缩后也占用两个字节的空间,又何必去多走一趟压缩算法耗费时间呢,直接输出就行了,所以最少三个字节才启动压缩。所以重复数据的数目不会存在0、1和2这三个数,那么咱就把它们用上让0对应3,1对应4,2对应5这样子,匹配范围于是从0到127变成了3到130。
四、RLE算法改进——对相似数据进行压缩
这种压缩方法来自于我对一篇论文的参考,下面也贴出这篇论文以表感谢,写的挺好的,通俗易懂。
[1]蓝波,林小竹,籍俊伟.一种改进的RLE算法在图像数据编码中的应用[J].微电子学与计算机,2004(05):101-103+107.
在这篇论文中,作者对这种改进的算法称为RLE-N算法,往往一想到RLE算法,我们都是去简单想到压缩数据中的重复数据值,但是往往在一幅图片中,不总是有很多重复的数据值存在的,更多的一种情况是相邻的数据虽然不重复,但是数据值非常的接近,从字节上面来看就是重复比特位有5到8个,不同的也就那几个比特位而已,既然这串数据的大部分比特位都是相同的,就那么一两个比特位不同,我们干脆就只记录这些会改变的比特位就是了,那些不变的我们只记录一次就行了。以上就是RLE-N的核心思想。下面从论文中摘抄一段文字来举个例子:
从图像的颜色分布看,在一幅图像中,如果两个像素点颜色相同或相近,表现在数值上为这两个像素的颜色值相等或相差很小,即一个字节的高位表示相似性,低位表示差异性。如果对两个字节进行从最高位到最低位比较,相应有高n位相同(n取值为0~8)九种情况。这样如果用标志位定义九种不同情况,需要4Bit来表示,那么一个字节中余下的4Bit表示行程长度,最多可以表示16个字节。高0位相同和RLE压缩算法中的不相同对应,高8位相同则表示两个字节完全相同。数据经过本算法处理后分为两部分:第一部分为一个字节,该字节的高位为标志位,低位表示行程长度;第二部分为数据。
我们先考虑一种简单的情况,假设标志位1000表示数据值全相同,0000表示数据值全不同,0100表示数据值高4位相同,其它情况暂不考虑。那么第二部分中,如果是相同颜色值的重复数据,则以一个字节表示该数据;如果是相近颜色值的数据串,数据值由相同部分和不同部分顺序连接而成,该部分的字节长度由所压缩数据串确定;如果颜色值完全不同,则原样排列。分析以下这一串数据:
则使用改进的RLE压缩算法可表示为:
压缩后的数据串中第1个、第3个和第8个字节分别为三个数据段的第一部分,也就是标志位和行程长度部分,紧跟在其后的是第二部分即数据部分。注意第四个字节0xC2, 其高四位为相近数据的相同部分0xC,而低四位即该数据的不同部分0x2;第五、六、七字节为其余六个相近数据不同部分的顺序组合。
以上就是这篇论文的核心思想了,大家可以抽时间看完全篇,接下来我实现的代码中,用一个字节中的高两位来区别匹配的比特数目,剩下的6个bit用来表示匹配的数目,同样启动压缩的阈值为3个字节,所以匹配数范围是3到66。
Python实现如下:
import ctypes
#输出1字节,其中高2位为标记,低6位为匹配数
class RLE():
def __init__(self):
self.threshold = 3 #启动压缩的阈值,大于这个阈值才有必要压缩
self.matchBitsToSign_T = {8:3, 6:2, 5:1} #匹配数到标记的映射
self.matchOrder = [8, 6, 5] #设置匹配顺序,即优先匹配多少字节
#比较两个字节中从高位开始的比特位匹配数,返回标记号
def cmpSameBits(self, byte1, byte2):
for matchBits in self.matchOrder:
if (byte1 >> (8 - matchBits)) == (byte2 >> (8 - matchBits)):
return self.matchBitsToSign_T[matchBits]
return 0
#文件压缩
def RLE_encode(self, readfilename, writefilename):
fread = open(readfilename, "rb")
fwrite = open(writefilename, "wb")
buf = b'' #前向缓冲区
bufSize = 63 + self.threshold #前向缓冲区大小
singleStore = b'' #无匹配的数据暂存区
singleStoreSize = 63 #无匹配的数据长度,没有加上阈值是因为匹配数可能小于阈值
buf = fread.read(bufSize - len(buf)) #尽可能将buf填满
while len(buf) >= self.threshold:
curIndex = 0 #当前匹配位置
cmpValue = self.cmpSameBits(buf[curIndex], buf[curIndex + 1]) #比较2个数据
if cmpValue != 0: #如果和下一个数据存在匹配关系
cmpValue2 = self.cmpSameBits(buf[curIndex + 1], buf[curIndex + 2]) #再往后比较两个数据
if cmpValue == cmpValue2: #如果还存在相同的匹配关系
curIndex += 1
#不断向下匹配具有相同匹配关系的数据
while ((curIndex + 2) < (len(buf))) and (cmpValue == self.cmpSameBits(buf[curIndex + 1], buf[curIndex + 2])):
curIndex += 1
# 相同的数据搜索完毕,如果之前有无匹配的数据没写入文件,先写入
if singleStore != b'':
fwrite.write(bytes(ctypes.c_uint8(len(singleStore))))
fwrite.write(singleStore)
singleStore = b''
fwrite.write(bytes(ctypes.c_uint8((cmpValue << 6) + curIndex + 2 - self.threshold))) #写入 标记+匹配数
bitsStore = 0 #比特位暂存区,相当于一个比特位队列
bitsCnt = 0 #比特位暂存区存在的比特位数目
for matchBits in self.matchBitsToSign_T: #寻找是哪一种匹配类型
if self.matchBitsToSign_T[matchBits] == cmpValue:
if matchBits == 8: #如果匹配数是8,特殊情况特殊处理
fwrite.write(bytes(ctypes.c_uint8(buf[0])))
else: #其他匹配数的处理都是有通性的
fwrite.write(bytes(ctypes.c_uint8(buf[0])))
for num in range(1, curIndex + 2): #将匹配的数据全部以比特位为单位进行编码
bitsStore += (((buf[num] << matchBits) & 0xFF) >> matchBits) << bitsCnt #处理完的比特位进入队列
bitsCnt += (8 - matchBits)
if bitsCnt >= 8: #队列中比特位数大于等于8了即一个字节,就可以输出一次到文件了
fwrite.write(bytes(ctypes.c_uint8(bitsStore & 0xFF)))
bitsStore >>= 8 #出队列
bitsCnt -= 8
break
if bitsCnt > 0: #将队列中剩余的数据写入文件
fwrite.write(bytes(ctypes.c_uint8(bitsStore & 0xFF)))
else:
singleStore += buf[curIndex: curIndex + 2]
buf = buf[curIndex + 2 : ] #从buf里清掉已经处理过的数据
else:
singleStore += buf[curIndex: curIndex + 1] #将1个不能匹配的数据加入暂存区
buf = buf[curIndex + 1:] #从buf里清掉已经处理过的数据
# 无匹配的数据存满了暂存区需要写入一次文件
if len(singleStore) >= singleStoreSize:
fwrite.write(bytes(ctypes.c_uint8(singleStoreSize)))
fwrite.write(singleStore[0:singleStoreSize])
singleStore = singleStore[singleStoreSize:]
buf += fread.read(bufSize - len(buf)) #尽可能将buf填满
singleStore += buf
# 无匹配的数据存满了暂存区需要写入一次文件
if len(singleStore) >= singleStoreSize:
fwrite.write(bytes(ctypes.c_uint8(singleStoreSize)))
fwrite.write(singleStore[0:singleStoreSize])
singleStore = singleStore[singleStoreSize:]
if singleStore != b'':
fwrite.write(bytes(ctypes.c_uint8(len(singleStore))))
fwrite.write(singleStore)
fread.close()
fwrite.close()
#文件解压
def RLE_decode(self, readfilename, writefilename):
fread = open(readfilename, "rb")
fwrite = open(writefilename, "wb")
sign = fread.read(1) #读取标记字节
while sign != b'':
if (sign[0] >> 6) == 0: #直接输出原始数据
buf = fread.read(sign[0])
fwrite.write(buf)
else:
for matchBits in self.matchBitsToSign_T: #寻找对应的匹配类型
if self.matchBitsToSign_T[matchBits] == (sign[0] >> 6):
if matchBits == 8: #特殊情况特殊处理
fwrite.write(fread.read(1) * ((sign[0] & 0x3F) + self.threshold))
else:
num = (sign[0] & 0x3F) + self.threshold #需要解压的数据个数
same = fread.read(1) #取一个模板数据
fwrite.write(same)
bitsStore = 0 #比特位队列
bitsCnt = 0 #记录比特位队列中比特位的数目
for i in range(1, num): #不断从比特位队列中解压出数据
if bitsCnt < (8 - matchBits):
tmp = fread.read(1)
if tmp == b'':
break
bitsStore += tmp[0] << bitsCnt
bitsCnt += 8
fwrite.write(bytes(ctypes.c_uint8(((same[0] >> (8 - matchBits)) << (8 - matchBits)) + (((bitsStore << matchBits) & 0xFF) >> matchBits))))
bitsStore >>= (8 - matchBits)
bitsCnt -= (8 - matchBits)
break
sign = fread.read(1) #读取下一个标记字节
fread.close()
fwrite.close()
if __name__ == '__main__':
Demo = RLE()
Demo.RLE_encode('random.txt', 'RLE-N.encode')
Demo.RLE_decode('RLE-N.encode', 'RLE-N.decode')五、压缩比性能测试
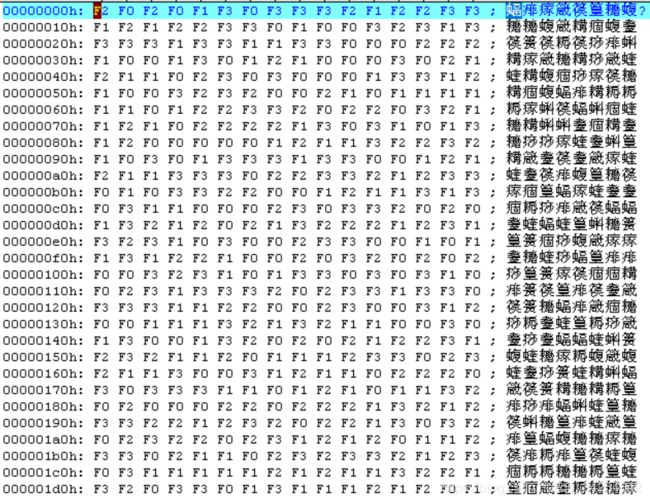
为了展示一下RLE-N这个算法的优点,做一个极端一点的测试,我生成了1个500KB的随机数文件,每个字节的大小范围是0xF0到0xF3,就是这些字节的高6位bit全部相同,只有低2位bit在变化,我截个图大概看一下数据情况:
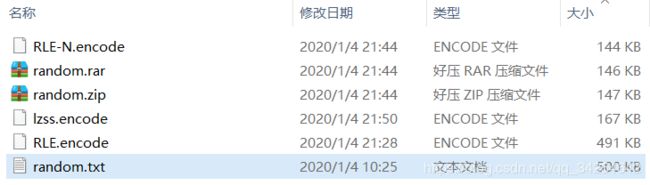
接下来展示一张压缩性能图:
其中random.txt是原始文件,RLE.encode是本文介绍的第一个RLE算法改进的压缩文件,lzss.encode是我上一篇博客所介绍的lzss算法的压缩文件,其中preBufSizeBits设置为3,random.zip是PC自带的ZIP压缩软件的压缩文件,random.rar是PC自带的RAR压缩软件的压缩文件,RLE-N.encode是采用RLE-N算法的压缩文件。因为我事先是知道这文件里面的数据特征的,所以原始文件里面的所有数据都被进行了6bit的匹配压缩,可见RLE-N在针对这种相似数据的压缩时,单从压缩比上来说甚至超过RAR。其实平常我们开发测试的时候有的测试数据也是有着这一类的特征的,这种压缩方法具有一定的实用性。
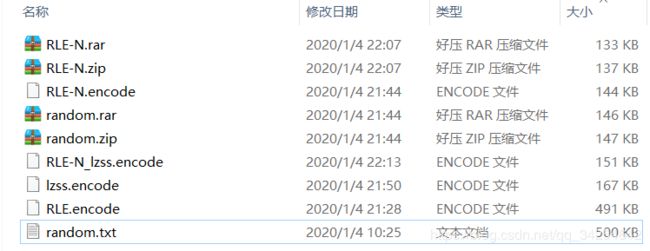
一般而言,RLE是对局部连续数据块的信息压缩,不会单独只使用RLE来对文件压缩就完了,因为全局的大方向上的信息还可以进行一轮压缩,所以一般还会再加一层压缩算法。带着好奇心的我又继续用LZSS、ZIP、RAR对RLE-N.encode进行压缩,看下最终效果:
二次压缩之后RAR的压缩比排在了第一位,ZIP次之,这就说明了RLE-N压缩后的文件仍然存在一定的可压缩空间;而用LZSS二次压缩后,文件反而还变大了。
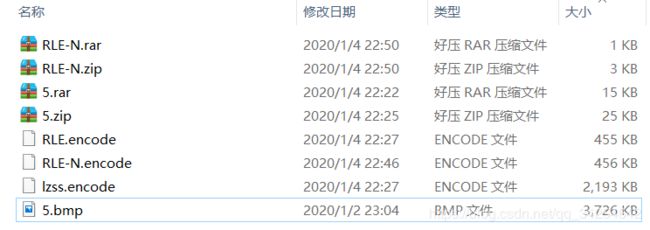
接下来再做一组测试,对一张横向渐变色的bmp图片进行压缩测试:
再附上性能图:
5.bmp是原始文件,因为数据时渐变的,所以单纯用LZSS算法压缩效果不太大,用RLE和RLE-N效果几乎一样,RAR在第一轮压缩中为15KB,在第二轮对RLE-N.encode的压缩后压缩文件大小居然变成了658字节。ZIP第二次压缩后压缩率也大幅度提高了。
六、总结
本文介绍了RLE算法的两种改进方法,展示了RLE-N算法在压缩相似性数据方面的优势。同时也通过对RLE算法的第一种改进和RLE-N算法的实现和对比实验,说明了在对相邻数据间相似性比较大的数据进行压缩时,先进行一遍RLE-N算法压缩,之后再进行一遍词典压缩,这样的复合压缩算法会具有更强的压缩性能。