在一般情况下,UIkit 使用的是左上角为原点的坐标系,mac 开发中使用左下角的坐标系,但是我们在ios开发中,难民啊会遇到坐标变换-transform
例如: [layer setAffineTransform: CGAffineTransformMakeScale(1, -1)];
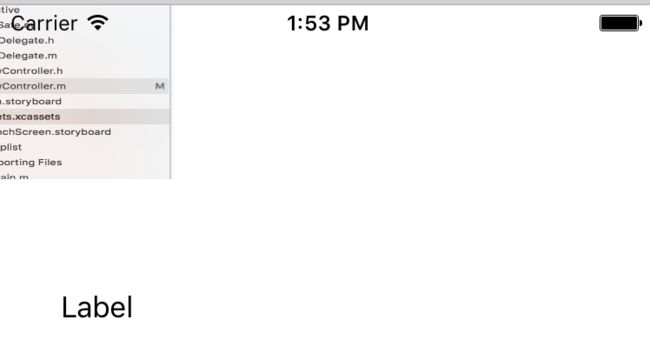
在该代码未执行前,如图:
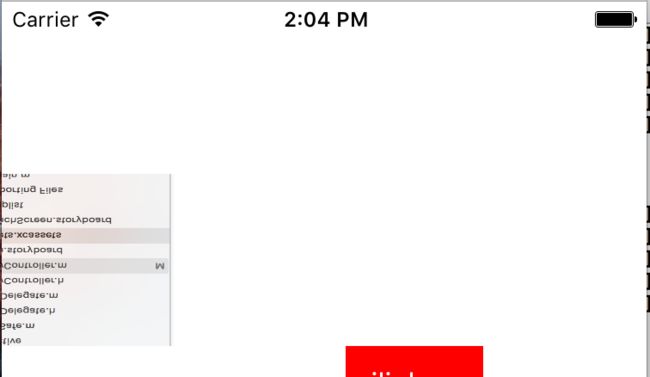
在执行上述代码之后:
我们发现,图片倒置了,这是为何?是因为这个layer得自身坐标系改变了
当我们继续处理
layer.affineTransform = CGAffineTransformTranslate(layer.affineTransform, 0, 100);
发现 屏幕上不会出现改layer,我们接着做一下改变
layer.affineTransform = CGAffineTransformTranslate(layer.affineTransform, 0, -100);
y坐标取负值才能显示出来!!!!
可是打印坐标信息如下
2016-01-17 14:03:35.953 JFReactive[65598:8234328] frame = {{0, 100}, {100, 100}}
2016-01-17 14:03:35.953 JFReactive[65598:8234328] bound = {{0, 0}, {100, 100}}
2016-01-17 14:03:35.954 JFReactive[65598:8234328] position ={50, 50}
2016-01-17 14:03:35.954 JFReactive[65598:8234328] anchorPoint ={0.5, 0.5}
从开始变换之前还是变换之后,坐标信息就没有改变,为何??(谁知道,告诉我!!!)
那这样的话,是不是可以理解为 layer的坐标系改变了呢?
我们先来看看仿设变化的推导公式
变化原理:源视图上的点p(x,y)变化成目标视图中p'(x',y')。对应关系为
x' = ax + cy + t(x) t(x) 代表下面的偏移值
y' = bx +dy +t(y)
由于scale 本质上是拉长或者缩短原来点与点之间的距离,所以可以推断出
x' = ax, y' = dy
这样应该是y坐标取负值,可是实际不是,这是为何?
我们先熟悉一下矩阵的
基本知识:
struct CGAffineTransform
{
CGFloat a, b, c, d;
CGFloat tx, ty;
};
CGAffineTransform CGAffineTransformMake (CGFloat a,CGFloat b,CGFloat c,CGFloat d,CGFloat tx,CGFloat ty);
为了把二维图形的变化统一在一个坐标系里,引入了齐次坐标的概念,即把一个图形用一个三维矩阵表示,其中第三列总是(0,0,1),用来作为坐标系的标准。所以所有的变化都由前两列完成。
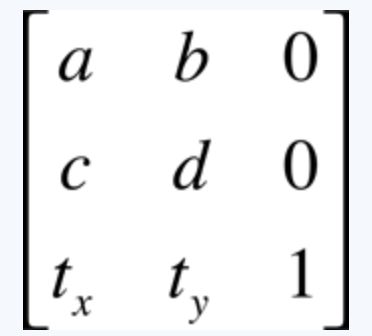
以上参数在矩阵中的表示为:
|a b 0|
|c d 0|
|tx ty 1|
运算原理:原坐标设为(X,Y,1);
|a b 0|
[X,Y, 1] |c d 0| = [aX + cY + tx bX + dY + ty 1] ;
|tx ty 1|
通过矩阵运算后的坐标[aX + cY + tx bX + dY + ty 1],我们对比一下可知:
第一种:设a=d=1, b=c=0.
[aX + cY + tx bX + dY + ty 1] = [X + tx Y + ty 1];
可见,这个时候,坐标是按照向量(tx,ty)进行平移,其实这也就是函数
CGAffineTransform CGAffineMakeTranslation(CGFloat tx,CGFloat ty)的计算原理。
第二种:设b=c=tx=ty=0.
[aX + cY + tx bX + dY + ty 1] = [aX dY 1];
可见,这个时候,坐标X按照a进行缩放,Y按照d进行缩放,a,d就是X,Y的比例系数,其实这也就是函数
CGAffineTransform CGAffineTransformMakeScale(CGFloat sx, CGFloat sy)的计算原理。a对应于sx,d对应于sy。
第三种:设tx=ty=0,a=cos?,b=sin?,c=-sin?,d=cos?。
[aX + cY + tx bX + dY + ty 1] = [Xcos? - Ysin? Xsin? + Ycos? 1] ;
可见,这个时候,?就是旋转的角度,逆时针为正,顺时针为负。其实这也就是函数
CGAffineTransform CGAffineTransformMakeRotation(CGFloat angle)的计算原理。angle即?的弧度表示。
问题:
为何scale(1,-1)不是我们预期的一样? y坐标应该是原来的y' = - y
参考链接:
http://ronnqvi.st/about-the-anchorpoint/