剑指offer(1-10题)详解
文章目录
- 01二维数组的查找
- 02替换空格
- 03从尾到头打印链表
- 04重建二叉树★
- 05 用两个栈实现队列
- 06旋转数组的最小数字
- 07 斐波那契数列
- 08 跳台阶
- 09 变态跳台阶★
- 10 矩阵覆盖
欢迎关注个人数据结构专栏哈
剑指offer系列:
剑指offer(1-10题)详解
剑指offer(11-25题)详解
剑指offer(26-33题)详解
剑指offer(34-40题)详解
剑指offer(41-50题)详解
剑指offer(51-59题)详解
剑指offer(60-67题)详解
微信公众号:bigsai
声明:大部分题基本未参考题解,基本为个人想法,如果由效率太低的或者错误还请指正!,如果有误导,还请指正!
01二维数组的查找
题目描述
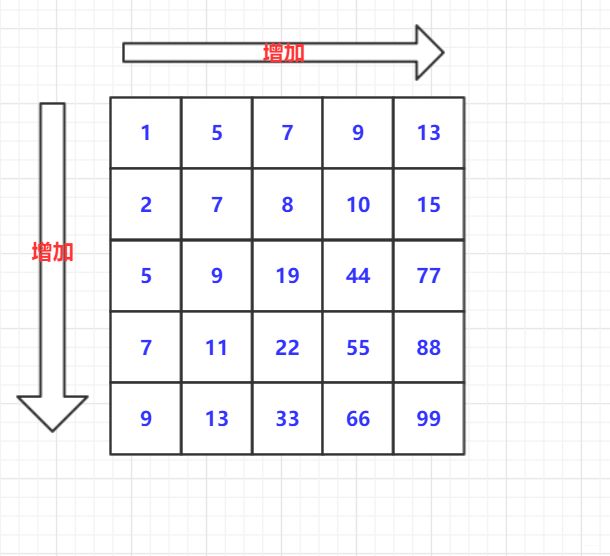
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
思路:
选定一个维度(行或列)先找到需要查找的元素所在的行(列),再从该行(列)找到该元素的该元素具体的列(行)位置。复杂度O(n)。
优化:因为数列是递增有序的,可以进行二分查找进行优化,但是本题可以不进行二分也可以过。因为大家有兴趣可以去查一查编程语言数组可以开多大。然后单个查找在这个范围内即使不优化也不会超时。有兴趣的可以自己写一写二分!复杂度O(logn)
public class Solution {
public boolean Find(int target, int [][] array) {
if(array.length==0||array[0].length==0)return false;
for(int i=array.length-1;i>=0;i--)
{
if(array[i][0]>target) {continue;}
for(int j=0;j<array[0].length;j++)
{
if(array[i][j]==target)
{return true;}
}
}
return false;
}
}
02替换空格
题目描述
请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
思路:
水题,字符串遍历重构即可。遇到为 的字符直接在新的字符添加一个%20即可。当然,在java中直接使用replaceAll即可。复杂度O(n);
ps: replaceall效率较低,建议使用StringBuider之类完成
参考讨论区:
在讨论区看到了一些不一样的声音,大致就是 有讨论是在原字符串上进行移动还是新建字符串的问题。当然新建字符串会更简单些,但是如果遇到要求在原字符串基础上进行移动的,因为String的底层实现是数组,那就要首先遍历一次知道有多少空格,然后扩充空间。至于遍历完空格的移动方式:从后往前移动的方式更好,因为最终移动的位置是相同的,但是从前往后每次遇到空格都会拖家带口后面一串都要跟着移动。(好比国旗下讲话排队往后挫,要挫很多次整体慢慢腾腾移动),而从后往前插就相当于很明确一个个明确移动到哪。
虽然两者最终已经总距离一样的,但是从前往后每个单词要经过(1-n)次才能移动到最后,而从后往前每个单词只1次就移动到目标位置!
代码:
public class Solution {
public static String replaceSpace(StringBuffer str) {
String team=str.toString();
return team.replaceAll(" ", "%20");
}
public static String replaceSpace(StringBuffer str) {//方法二
StringBuffer str2 = new StringBuffer();
char demo = ' ';
for (int i = 0; i < str.length(); i++) {
demo = str.charAt(i);
if (demo == ' ') {
str2.append("%20");
} else {
str2.append(demo);
}
}
return str2.toString();
}
}
03从尾到头打印链表
题目描述
输入一个链表,按链表从尾到头的顺序返回一个ArrayList。
思路:
题目给我们一个链表让我们返回一个序列数字。而这个序列要求我们将链表从后向前的顺序返回。当然,这样的话处理方法就比较多了。比如先从前往后存到一个数组中,然后数组再从后往前往List中塞。
当然Arraylist本身也是一个线性表(顺序表),可以进行头插。将链表每次向后遍历的数插在首位,最后返回即可。
/**
* public class ListNode {
* int val;
* ListNode next = null;
*
* ListNode(int val) {
* this.val = val;
* }
* }
*
*/
import java.util.ArrayList;
public class Solution {
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
ArrayList<Integer>list=new ArrayList<Integer>();
while (listNode!=null) {
list.add(0, listNode.val);
listNode=listNode.next;
}
return list;
}
}
参考讨论区:
这题参考了讨论区,发现了一些其他比较优秀的解法,比如可以用递归函数进行插入,当next为null的时候停止,当然还有就是利用栈的结构储存然后抛出啦。这些思想都可实现!
04重建二叉树★
题目描述
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
思路:
说实话这题还是有难度的,以前手动模拟的时候也没掌握方法只是瞎画。以前再力扣也曾经遇到这题当时不会停滞下来。不过这次凭借思考还是克服了。
我们都知道一个中序序列带着一个前序或者后序序列都能确定一棵完整的二叉树。首先分析这种问题。二叉树的问题大部分有可重复性,经常会使用递归。所以大部分人应该能够想到使用递归,但是可能不清楚该怎么递归。其实递归的使用不需要你考虑全篇,需要你谨慎完整的考虑其中一个过程。现在我们看看前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},的构造过程!
- 对于前序,我们知道从根还是,所以可以确定第一个是根。然而中序是
左中右。我们找到根的位置,那么我们就可以确定这个根的左侧是左侧,根的右侧是二叉树的右侧。 - 然而很重要的一点是:在中序左侧右侧的在前序序列中的:根
左右。虽然具体排序可能不同,但是左区域、右区域(区域元素总数量)也是连续的,所以我们这样可以确定唯一一个根,然后前序有左右两个区域,中序有左右两个区域,这样递归的构造子树,知道完成二叉排序树。 - 所以,如果用代码实现的话,比较麻烦的就是要考率数组的区间问题,要记录进行复原的两数组的左右区间。具体理解还是要靠大家。
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
TreeNode node=new TreeNode(in[0]);//根节点
int preleft=0,preright=pre.length-1;
int inleft=0,inright=pre.length-1;
return creat(pre, in, preleft, preright,inleft,inright);
}
private TreeNode creat(int[] pre, int[] in, int preleft, int preright, int inleft, int inright) {
if(preleft>preright||inleft>inright)return null;
TreeNode node=new TreeNode(pre[preleft]);
int mid=0;
for(int i=inleft;i<=inright;i++)
{
if(pre[preleft]==in[i])
{
mid=i;
}
}
node.left=creat(pre, in, preleft+1, preleft+(mid-inleft), inleft, mid-1);
node.right=creat(pre, in, preleft+(mid-inleft)+1, preright, mid+1, inright);
return node;
}
}
05 用两个栈实现队列
题目描述
用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型
思路:
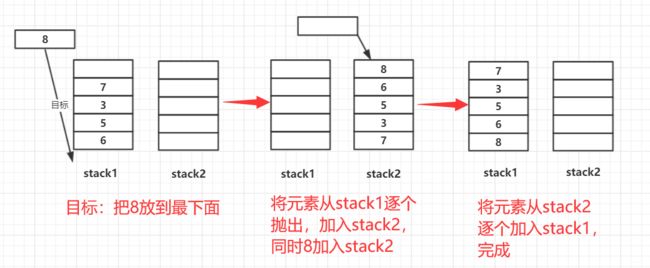
首先要了解队列,队列是一种先进先出(排队)的结构,而栈是一种后进先出的结构。如果基本概念不清可以看我以前写的哈。要求完成push和pop两种操作。push就是加入队尾(tail)类似enqueue,而pop是返回并抛出队头(front)类似dequeue。我们假设stack1是用作返回,而stack2用作中转。可以先看看下面的图。假设7、3、5、6在队列中,待加入8(push8).
- stack1用作返回,那么栈顶肯定是队头(才能返回),在不发生变化的状态甚至是pop返回的状态是这样的:
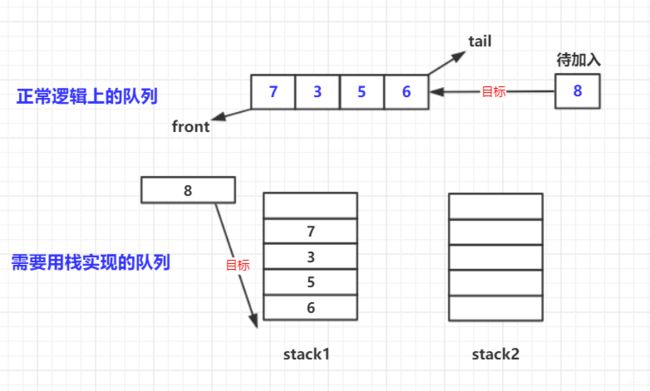
- 对于push加入的操作,两个栈,处理思路就是先用栈2倒置栈1,然后加入要加入的元素到栈2,再用栈1倒置栈2。
实现代码为:
import java.util.Stack;
public class Solution {
Stack<Integer> stack1 = new Stack<Integer>();
Stack<Integer> stack2 = new Stack<Integer>();
public void push(int node) {
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
stack2.push(node);
while (!stack2.isEmpty()) {
stack1.push(stack2.pop());
}
stack2.clear();
}
public int pop() {
return stack1.pop();
}
}
06旋转数组的最小数字
题目描述
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
思路:
就是要求我们在这么一组序列中找到最小的一个数字,非递减的旋转,也就是这么一串有两段非递减的连续串串。找到第二个非递减的串串头就是结果。
然而,我们只需第一次查找到最小即可结束。不会超时还是因为数组大小有限制。无法提供更大量输入数据。复杂度为O(n);
public int minNumberInRotateArray(int [] array) {
if(array.length==0)return 0;
int min=array[0];
for(int i=0;i<array.length;i++)
{
if(array[i]<min)
{
min=array[i];
break;
}
}
return min;
}
参考题解:
之前提过二分,但是这题很多讨论区的方案并非完善,漏了非递减比如101111这种情况。而二分也只是压缩搜索空间,如归一个非递减串被分成左侧非递减和右侧非递减,右侧的最大要小于等于左侧最小的。就跟就行分类讨论,下面分享一个讲的不错的题解(原文链接):
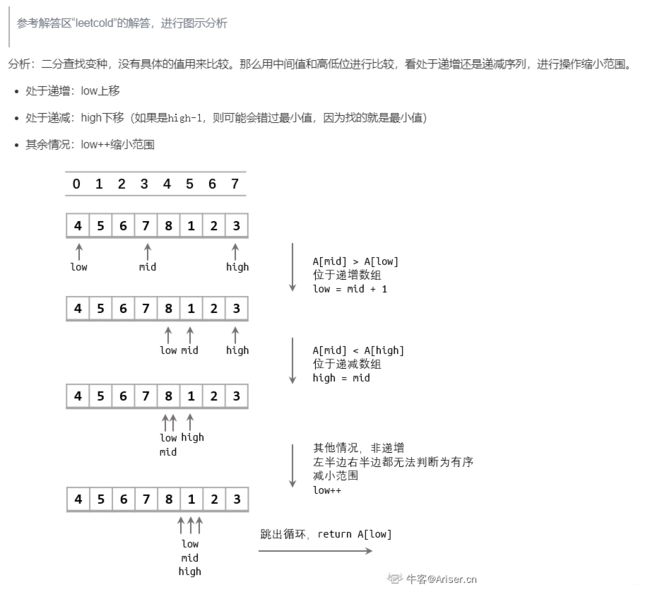
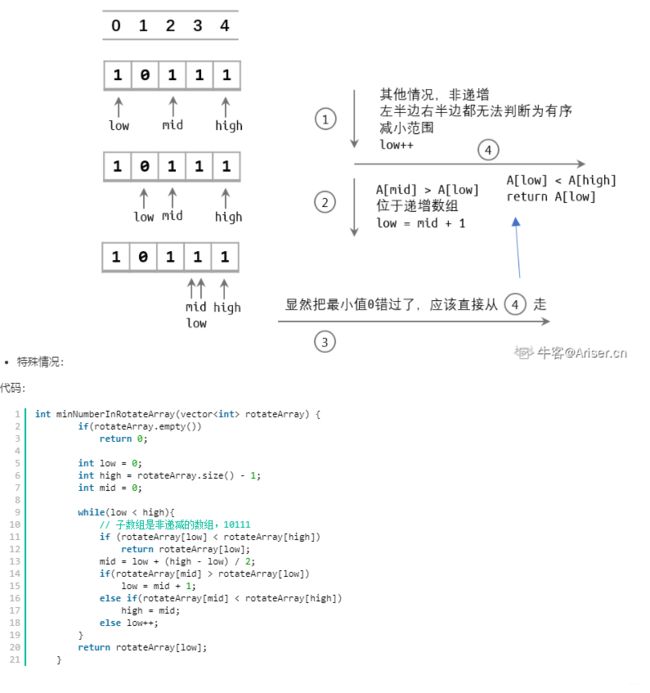
07 斐波那契数列
题目描述
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。
n<=39
思路:斐波那契的公式为:
F(0)=0;F(1)=1;
F(n)=F(n-1)+F(n-2); (n>=2)
你可以使用递归,但是递归效率极低!因为递归的一项会产生新的两项递归函数。它的复杂度是O(2n)指数级别的。具体原因可以参考以前的一篇文章的动态图递归详解。这里不做累述。因为递归浪费太多资源,进行很多没必要的运算。所以我们采用数组从前往后计算。两种方法都附上代码。
代码为(推荐法2):
public int Fibonacci(int n) {
if (n == 1 || n == 0) {
return n;
} else {
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
}
/*
* 法二,打表法
*/
public int Fibonacci2(int n) {
int Fibo[]=new int [40];
Fibo[0]=0;
Fibo[1]=1;
for(int i=2;i<=n;i++)
{
Fibo[i]=Fibo[i-1]+Fibo[i-2];
}
return Fibo[n];
}
参考讨论区:
其他的其实没有多少区别的,主要是动态规划从前往后计算不需要整个数组。只需要两个变量就够了,这样空间能够节省一些。

08 跳台阶
题目描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
思路:
可以递归或者dp吧,因为当前台阶F(n)可能是1步跳来的,也可能是2步跳来的。所以F(n)=F(n-1)+F(n-2).(初始情况单独考虑)。这题递归和正向dp时间复杂度差不多,区别不大。
代码为:
public int JumpFloor(int target) {
int dp[]=new int[target+1];
dp[0]=1;
dp[1]=1;
for(int i=2;i<=target;i++)
{
dp[i]=dp[i-1]+dp[i-2];
}
return dp[target];
}
参考评论区:
本题评论区的有些递归方案感觉感觉不太好,只有优化和斐波那契差不多,可以用两个数进行计算就可以了,节省部分空间。
09 变态跳台阶★
题目描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
思路:
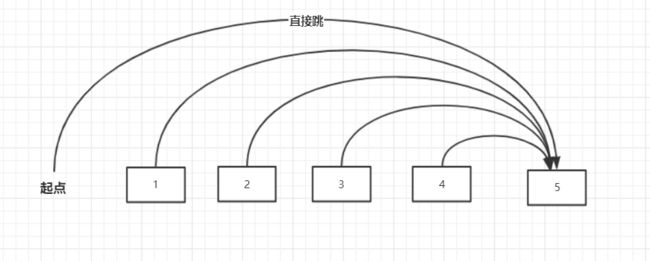
这种复杂的就别想着用递归了,从正面考虑吧。对于n位置的跳法,可能从n-1跳,可能从n-2跳-------可能从1跳,也可能直接从开始跳。所以F(n)=1(直接跳)+sum(F(k)) (k属于1到n-1)。我们肯定需要一个数组储存F[n];但是我们不能每次都要相加。所以用一个sum[]数组储存前n个跳法的合即可!
代码:
public class Solution {
public int JumpFloorII(int target) {
int a[]=new int[target+1];//存储结果
int sum[]=new int[target+1];//储存和
a[1]=1;
sum[1]=1;
for(int i=2;i<=target;i++)
{
a[i]=1+sum[i-1];
sum[i]=a[i]+sum[i-1];
}
return a[target];
}
}
参考评论区:
这题,个人分析方法是基于常规算法的,看了讨论区有个非常非常牛的用数学推理方法,类似等差等比数列的推理,做题的时候没想到直接这么推哈哈,大家可以学习一波!


10 矩阵覆盖
题目描述
我们可以用2 * 1 的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2 * 1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
思路:
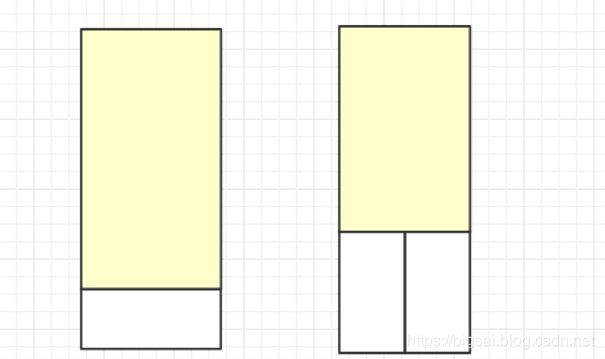
递归或dp。每个矩形的大小都是2*1;同样第F(n)=F(n-1)+F(n-2).(第n-1个横铺一块,第n-2竖直两块)考虑下初始即可
代码为:
/*
* dp
*/
public int RectCover(int target) {
if(target==0)return 0;
int dp[]=new int[target+1];
dp[0]=1;
dp[1]=1;
for(int i=2;i<=target;i++)
{
dp[i]=dp[i-1]+dp[i-2];
}
return dp[target];
}
/*
* 递归
*/
// public int RectCover(int target) {
// if(target==0)return 0;
// if(target==1)return 1;
// if(target==2)return 2;
// else {
// return RectCover(target-1)+RectCover(target-2);
// }
// }
欢迎关注、交流,微信公众号:bigsai!