Python 机器学习经典实例

内容介绍

在如今这个处处以数据驱动的世界中，机器学习正变得越来越大众化。它已经被广泛地应用于不同领域，如搜索引擎、机器人、无人驾驶汽车等。本书首先通过实用的案例介绍机器学习的基础知识，然后介绍一些稍微复杂的机器学习算法，例如支持向量机、极端随机森林、隐马尔可夫模型、条件随机场、深度神经网络，等等。

用最火的Python语言、通过各种各样的机器学习算法来解决实际问题！书中介绍的主要问题如下。

• 探索分类分析算法并将其应用于收入等级评估问题
• 使用预测建模并将其应用到实际问题中
• 了解如何使用无监督学习来执行市场细分
• 探索数据可视化技术以多种方式与数据进行交互
• 了解如何构建推荐引擎
• 理解如何与文本数据交互并构建模型来分析它
• 使用隐马尔科夫模型来研究语音数据并识别语音

作者简介

Prateek Joshi，人工智能专家，重点关注基于内容的分析和深度学习，曾在英伟达、微软研究院、高通公司以及硅谷的几家早期创业公司任职。

课程内容

译者序

有一天，忽然想到自己整天面对着52个英文字母、9个数字、32个符号^①和一个空格，经常加班没有双休日，好傻。时间不断被各种噪声碎片化，完全就是毛姆在《月亮和六便士》里写的，“If you look on the ground in search of a sixpence, you don't look up, and so miss the moon”，整天低头刷手机，却不记得举头望明月。生活也愈发无序，感觉渐渐被掏空。薛定谔的《生命是什么》给我提了个醒，他在“以‘负熵’为生”（It Feeds On ‘negative Entropy’）一节指出：“要活着，唯一的办法就是从环境里不断地汲取负熵。”在介绍了熵的概念及其统计学意义之后，他紧接着在“从环境中引出‘有序’以维持组织”（Organization Maintained By Extracting ‘Order’From The Environment）一节进一步总结：“一个有机体使本身稳定在较高的有序水平上（等于熵的相当低的水平上）的办法，就是从环境中不断地吸取秩序。”这个秩序（负熵、klog(1/n)）可以是食物，也可以是知识，按主流叫法就是“正能量”（有些所谓正能量却碰巧是增加系统无序水平的正熵）。于是，我开始渐渐放弃那些让人沮丧的老梗，远离那些引发混乱的噪声，重新读书，试着翻译，学会去爱。这几年最大的收获就是明白了“隔行如隔山”的道理，试着循序渐进，教学相长，做力所能及之事，让编程变简单。

一般人都不喜欢编程，更不喜欢动手编程（时间消耗：编写 & 测试 40%、重构 40%、风格 & 文档 20%），却喜欢在心里、嘴上编程：“先这样，再那样，如果要 XX，就 YY，最后就可以 ZZ 了。”分分钟就可以说完几万行代码的项目，水还剩大半杯。一旦大期将近，即使要亲自动手 Copy 代码，也会觉得苦堪搬砖，键盘不是红与黑、屏幕不能左右推、小狗总是闹跑追，不断在数不清的理由中增加自己的熵。偶尔看编程书的目的也很明确，就是为了快速上手，找到答案。当然也是在 Google、StackOverflow、GitHub 网站上找不到答案之后，无可奈何之举。编程书把看着复杂的知识写得更复杂，虽然大多篇幅不输“飞雪连天射白鹿，笑书神侠倚碧鸳”等经典，且纲举目张、图文并茂，甚至有作者爱引经据典，却极少有令人拍案的惊奇之处。为什么同样是文以载道，编程书却不能像武侠小说一样简单具体，反而显得了无生趣，令人望而却步？虽然编程的目的就是用计算机系统解决问题，但是大多数问题的知识都在其他领域中，许多作者在介绍编程技巧时，又试图介绍一些并不熟悉的背景知识，显得生涩难懂，且增加了书的厚度。

有时我们真正需要的，就是能快刀斩乱麻的代码。（Talk is cheap, show me the code.）编程与研究数理化不同，没有任何假设、原命题、思维实验，并非科学；与舞剑、奏乐、炒菜相似，都是手艺，只要基础扎实，便结果立判。编程技巧也可以像剑谱、乐谱、食谱一般立竿见影，这本《Python 机器学习经典实例》正是如此，直接上代码，照着做就行，不用纠结为什么。

机器学习是交叉学科，应用广泛，目前主流方法为统计机器学习。既然是以统计学为基础，那么就不只是计算机与数学专业的私房菜了，机器学习在自然科学、农业科学、医药科学、工程与技术科学、人文与社会科学等多种学科中均可应用。如果你遇到了回归、分类、预测、聚类、文本分析、语音识别、图像处理等经典问题，需要快速用 Python 解决，那么这本菜谱适合你。即使你对机器学习方法还一知半解，也不妨一试。毕竟是 Python 的机器学习，还能难到哪儿去呢？目前十分流行的 Python 机器学习库 scikit-learn 是全书主角之一，功能全面，接口友好，许多经典的数据集和机器学习案例都来自Kaggle^②。若有时间追根溯源，请研究周志华教授的《机器学习》西瓜书，周教授啃着西瓜把机器学习调侃得淋漓尽致，详细的参考文献尤为珍贵。但是想当作菜谱看，拿来就用，还是需要费一番功夫；若看书不过瘾，还有吴恩达（Andrew Ng）教授在Coursera上的机器学习公开课^③，机器学习入门最佳视频教程，吴教授用的工具是 Matlab 的免费开源版本 Octave，你也可以用 Python 版演示教学示例。

学而时习之，不亦乐乎。学习编程技巧，解决实际问题，是一件快乐的事情。希望这本 Python 机器学习经典案例，可以成为你的负熵，帮你轻松化解那些陈年老梗。如果再努努力，也许陆汝钤院士在《机器学习》序言中提出的6个问题^④，你也有答案了。

示例代码：

"""打印ASCII字母表、数字、标点符号"""import stringfor item in [string.ascii_letters,             string.digits,             string.punctuation]:    print('{}\t{}'.format(len(item), item))

输出结果：

52 abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ10 012345678932 !"#$%&'()*+,-./:;<=>?@[\]^_`{|}~

①见文末Python示例代码。

②Kaggle 是一个2010年成立的数据建模和数据分析竞赛平台，全球数据科学家、统计学家、机器学习工程师的聚集地，上面有丰富的数据集，经典的机器学习基础教程，以及让人流口水的竞赛奖金，支持Python、R、Julia、SQLite，同时也支持 jupyter notebook 在线编程环境，2017年3月8日被谷歌收购。

③分免费版和付费版（购买结业证书），学习内容一样。

④陆院士的6个问题分别是：1. 机器学习早期的符号机器学习，如何在统计机器学习主流中发展；2. 统计机器学习算法中并不现实的“独立同分布”假设如何解决；3. 深度学习得益于硬件革命，是否会取代统计机器学习；4. 机器学习用的都是经典的概率统计、代数逻辑，而目前仅有倒向微分方程用于预测，微分几何的流形用于降维，只是数学领域的一角，其他现代数学理论是否可以参与其中；5. 机器学习方法仍不够严谨，例如目前流形学习直接将高维数据集假设成微分流形，需要进一步完善；6. 大数据与统计机器学习是如何互动的。

流形学习，Manifold learning，科普见此。

前言

在如今这个处处以数据驱动的世界中，机器学习正变得越来越大众化。它已经被广泛地应用于不同领域，如搜索引擎、机器人、无人驾驶汽车等。本书不仅可以帮你了解现实生活中机器学习的应用场景，而且通过有趣的菜谱式教程教你掌握处理具体问题的算法。

本书首先通过实用的案例介绍机器学习的基础知识，然后介绍一些稍微复杂的机器学习算法，例如支持向量机、极端随机森林、隐马尔可夫模型、条件随机场、深度神经网络，等等。本书是为想用机器学习算法开发应用程序的 Python 程序员准备的。它不仅适合 Python 初学者（当然，熟悉 Python 编程方法将有助于体验示例代码），而且也适合想要掌握机器学习技术的 Python 老手。

通过本书，你不仅可以学会如何做出合理的决策，为自己选择合适的算法类型，而且可以学会如何高效地实现算法以获得最佳学习效果。如果你在图像、文字、语音或其他形式的数据处理中遇到困难，书中处理这些数据的机器学习技术一定会对你有所帮助！

本书内容

第1章介绍各种回归分析的监督学习技术。我们将学习如何分析共享自行车的使用模式，以及如何预测房价。

第2章介绍各种数据分类的监督学习技术。我们将学习如何评估收入层级，以及如何通过特征评估一辆二手汽车的质量。

第3章论述支持向量机的预测建模技术。我们将学习如何使用这些技术预测建筑物里事件发生的概率，以及体育场周边道路的交通情况。

第4章阐述无监督学习算法，包括 K-means 聚类和均值漂移聚类。我们将学习如何将这些算法应用于股票市场数据和客户细分。

第5章介绍推荐引擎的相关算法。我们将学习如何应用这些算法实现协同滤波和电影推荐。

第6章阐述与文本数据分析相关的技术，包括分词、词干提取、词库模型等。我们将学习如何使用这些技术进行文本情感分析和主题建模。

第7章介绍与语音数据分析相关的算法。我们将学习如何建立语音识别系统。

第8章介绍分析时间序列和有序数据的相关技术，包括隐马尔可夫模型和条件随机场。我们将学习如何将这些技术应用到文本序列分析和股市预测中。

第9章介绍图像内容分析与物体识别方面的算法。我们将学习如何提取图像特征，以及建立物体识别系统。

第10章介绍在图像和视频中检测与识别面部的相关技术。我们将学习使用降维算法建立面部识别器。

第11章介绍建立深度神经网络所需的算法。我们将学习如何使用神经网络建立光学文字识别系统。

第12章介绍机器学习使用的数据可视化技术。我们将学习如何创建不同类型的图形和图表。

阅读背景

Python 2.x 和 Python 3.x 的版本之争尚未平息^①。一方面，我们坚信世界会向更好的版本不断进化，另一方面，许多开发者仍然喜欢使用 Python 2.x 的版本。目前许多操作系统仍然内置 Python 2.x。本书的重点是介绍 Python 机器学习，而非 Python 语言本身。另外，考虑到程序的兼容性，书中用到了一些尚未被迁移到 Python 3.x 版本的程序库，因此，本书依然选择 Python 2.x 的版本。我们会尽最大努力保持代码兼容各种 Python 版本，因为这样可以让你轻松地理解代码，并且很方便地将代码应用到不同场景中。

读者对象

本书是为想用机器学习算法开发应用程序的 Python 程序员准备的。它适合 Python 初学者阅读，不过熟悉 Python 编程方法对体验示例代码大有裨益。

内容组织

在本书中，你会频繁地看到下面这些标题（准备工作、详细步骤、工作原理、更多内容、另请参阅）。

为了更好地呈现内容，本书采用以下组织形式。

准备工作

这部分首先介绍本节目标，然后介绍软件配置方法以及所需的准备工作。

详细步骤

这部分介绍具体的实践步骤。

工作原理

这部分通常是对前一部分内容的详细解释。

更多内容

这部分会补充介绍一些信息，帮助你更好地理解前面的内容。

另请参阅

这部分提供一些参考资料。

排版约定

在本书中，你会发现一些不同的文本样式。这里举例说明它们的含义。

嵌入代码、命令、选项、参数、函数、字段、属性、语句等，用等宽的代码字体显示：“这里，我们将25%的数据用于测试，可以通过test_size参数进行设置。”

代码块用如下格式：

import numpy as npimport matplotlib.pyplot as pltimport utilities# Load input datainput_file = 'data_multivar.txt'X, y = utilities.load_data(input_file)

命令行输入或输出用如下格式：

$ python object_recognizer.py --input-image imagefile.jpg --model-fileerf.pkl --codebook-file codebook.pkl

新术语和重要文字将采用黑体字。你在屏幕上看到的内容，包括对话框或菜单里的文本，都将这样显示：“如果你将数组改为(0, 0.2, 0, 0, 0)，那么 Strawberry 部分就会高亮显示。”

读者反馈

我们非常欢迎读者的反馈。如果你对本书有些想法，有什么喜欢或是不喜欢的，请反馈给我们，这将有助于我们出版充分满足读者需求的图书。

一般性反馈请发送电子邮件至 [email protected]，并在邮件主题中注明书名。

如果你在某个领域有专长，并有意编写一本书或是贡献一份力量，请参考我们的作者指南。

客户支持

你现在已经是引以为傲的 Packt 读者了。为了能让你的购买物超所值，我们还为你准备了以下内容。

下载示例代码

你可以用你的账户从此处下载所有已购买 Packt 图书的示例代码文件。如果你是从其他途径购买的本书，可以访问此处并注册，我们将通过电子邮件把文件发送给你。

可以通过以下步骤下载示例代码文件：

(1) 用你的电子邮件和密码登录或注册我们的网站；

(2) 将鼠标移到网站上方的客户支持（SUPPORT）标签；

(3) 单击代码下载与勘误（Code Downloads & Errata）按钮；

(4) 在搜索框（Search）中输入书名；

(5) 选择你要下载代码文件的书；

(6) 从下拉菜单中选择你的购书途径；

(7) 单击代码下载（Code Download）按钮。

你也可以通过单击 Packt 网站上本书网页上的代码文件（Code Files）按钮来下载示例代码，该网页可以通过在搜索框（Search）中输入书名获得。以上操作的前提是你已经登录了 Packt 网站。

下载文件后，请确保用以下软件的最新版来解压文件：

• WinRAR / 7-Zip for Windows ；

• Zipeg / iZip / UnRarX for Mac ；

• 7-Zip / PeaZip for Linux 。

本书的代码包也可以在 GitHub 上获得。另外，我们在这里还有其他书的代码包和视频，请需要的读者自行下载。

下载本书的彩色图片

我们也为你提供了一份 PDF 文件，里面包含了书中的截屏和图表等彩色图片，彩色图片能帮助你更好地理解输出的变化。下载地址

勘误

虽然我们已尽力确保本书内容正确，但出错仍旧在所难免。如果你在书中发现错误，不管是文本还是代码，希望能告知我们，我们将不胜感激。这样做，你可以使其他读者免受挫败，也可以帮助我们改进本书的后续版本。如果你发现任何错误，请访问这里，选择本书，单击勘误表提交表单（Errata Submission Form）的链接，并输入详细说明。^②勘误一经核实，你提交的内容将被接受，此勘误会上传到本公司网站或添加到现有勘误表。

访问这里，在搜索框中输入书名，可以在勘误（Errata）部分查看已经提交的勘误信息。

盗版

任何媒体都会面临版权内容在互联网上的盗版问题，Packt 也不例外。Packt 非常重视版权保护。如果你发现我们的作品在互联网上被非法复制，不管以什么形式，都请立即为我们提供相关网址或网站名称，以便我们寻求补救。

请把可疑盗版材料的链接发到 [email protected]。

保护我们的作者，就是保护我们继续为你带来价值的能力，我们将不胜感激。

问题

如果你对本书内容存有疑问，不管是哪个方面的，都可以通过 [email protected] 联系我们，我们会尽最大努力解决。

①2020年之前应该不会终结。——译者注

②中文版勘误可以到这里查看和提交。——编者注

第01章：监督学习（上）

在这一章，我们将介绍以下主题：

• 数据预处理技术

• 标记编码方法

• 创建线性回归器（linear regressor）

• 计算回归准确性

• 保存模型数据

• 创建岭回归器（ridge regressor）

• 创建多项式回归器（polynomial regressor）

• 估算房屋价格

• 计算特征的相对重要性

• 评估共享单车的需求分布

1.1　简介

如果你熟悉机器学习的基础知识，那么肯定知道什么是监督学习。监督学习是指在有标记的样本（labeled samples）上建立机器学习的模型。例如，如果用尺寸、位置等不同参数建立一套模型来评估一栋房子的价格，那么首先需要创建一个数据库，然后为参数打上标记。我们需要告诉算法，什么样的参数（尺寸、位置）对应什么样的价格。有了这些带标记的数据，算法就可以学会如何根据输入的参数计算房价了。

无监督学习与刚才说的恰好相反，它面对的是没有标记的数据。假设需要把一些数据分成不同的组别，但是对分组的条件毫不知情，于是，无监督学习算法就会以最合理的方式将数据集分成确定数量的组别。我们将在后面章节介绍无监督学习。

建立书中的各种模型时，将使用许多 Python 程序包，像 NumPy、SciPy、scikit-learn、matplotlib 等。如果你使用 Windows 系统，推荐安装兼容 SciPy 关联程序包的 Python 发行版，这些 Python 发行版里已经集成了常用的程序包。如果你使用 Mac OS X 或者 Ubuntu 系统，安装这些程序包就相当简单了。下面列出来程序包安装和使用文档的链接：

• NumPy：http://docs.scipy.org/doc/numpy-1.10.1/user/install.html

• SciPy：http://www.scipy.org/install.html

• scikit-learn：http://scikit-learn.org/stable/install.html

• matplotlib：http://matplotlib.org/1.4.2/users/installing.html

现在，请确保你的计算机已经安装了所有程序包。

1.2　数据预处理技术

在真实世界中，经常需要处理大量的原始数据，这些原始数据是机器学习算法无法理解的。为了让机器学习算法理解原始数据，需要对数据进行预处理。

1.2.1　准备工作

来看看 Python 是如何对数据进行预处理的。首先，用你最喜欢的文本编辑器打开一个扩展名为.py 的文件，例如 preprocessor.py。然后在文件里加入下面两行代码：

import numpy as npfrom sklearn import preprocessing

我们只是加入了两个必要的程序包。接下来创建一些样本数据。向文件中添加下面这行代码：

data = np.array([[3,  -1.5,    2,  -5.4], [0,    4,    -0.3,  2.1], [1,    3.3,-1.9, -4.3]])

现在就可以对数据进行预处理了。

1.2.2　详细步骤

数据可以通过许多技术进行预处理，接下来将介绍一些最常用的预处理技术。

1.均值移除（Mean removal）

通常我们会把每个特征的平均值移除，以保证特征均值为0（即标准化处理）。这样做可以消除特征彼此间的偏差（bias）。将下面几行代码加入之前打开的Python文件中：

    data_standardized = preprocessing.scale(data)    print "\nMean =", data_standardized.mean(axis=0)    print "Std deviation =", data_standardized.std(axis=0)

现在来运行代码。打开命令行工具，然后输入以下命令：

    $ python preprocessor.py命令行工具中将显示以下结果：    Mean = [  5.55111512e-17  -1.11022302e-16  -7.40148683e-17  -7.40148683e-17]    Std deviation = [ 1.  1.  1.  1.]你会发现特征均值几乎是`0`，而且标准差为`1`。

2.范围缩放（Scaling）

数据点中每个特征的数值范围可能变化很大，因此，有时将特征的数值范围缩放到合理的大小是非常重要的。在 Python 文件中加入下面几行代码，然后运行程序：

    data_scaler = preprocessing.MinMaxScaler(feature_range=(0, 1))    data_scaled = data_scaler.fit_transform(data)    print "\nMin max scaled data =", data_scaled

范围缩放之后，所有数据点的特征数值都位于指定的数值范围内。输出结果如下所示：

    Min max scaled data:    [[ 1.            0.            1.            0.        ]     [ 0.            1.            0.41025641    1.        ]     [ 0.33333333    0.87272727    0.            0.14666667]]

3.归一化（Normalization）

数据归一化用于需要对特征向量的值进行调整时，以保证每个特征向量的值都缩放到相同的数值范围。机器学习中最常用的归一化形式就是将特征向量调整为 L1范数，使特征向量的数值之和为1。增加下面两行代码到前面的 Python 文件中：

    data_normalized = preprocessing.normalize(data, norm='l1')    print "\nL1 normalized data =", data_normalized

执行 Python 文件，就可以看到下面的结果：

    L1    normalized    data:    [[    0.25210084    -0.12605042    0.16806723    -0.45378151]     [    0.             0.625        -0.046875       0.328125  ]     [    0.0952381      0.31428571   -0.18095238    -0.40952381]]

这个方法经常用于确保数据点没有因为特征的基本性质而产生较大差异，即确保数据处于同一数量级，提高不同特征数据的可比性。

4.二值化（Binarization）

二值化用于将数值特征向量转换为布尔类型向量。增加下面两行代码到前面的 Python 文件中：

    data_binarized = preprocessing.Binarizer(threshold=1.4).transform(data)    print "\nBinarized data =", data_binarized

再次执行 Python 文件，就可以看到下面的结果：

    Binarized data:    [[    1.    0.    1.    0.]     [    0.    1.    0.    1.]     [    0.    1.    0.    0.]]

如果事先已经对数据有了一定的了解，就会发现使用这个技术的好处了。

5.独热编码

通常，需要处理的数值都是稀疏地、散乱地分布在空间中，然而，我们并不需要存储这些大数值，这时就需要使用独热编码（One-Hot Encoding）。可以把独热编码看作是一种收紧（tighten）特征向量的工具。它把特征向量的每个特征与特征的非重复总数相对应，通过 one-of-k 的形式对每个值进行编码。特征向量的每个特征值都按照这种方式编码，这样可以更加有效地表示空间。例如，我们需要处理4维向量空间，当给一个特性向量的第 n 个特征进行编码时，编码器会遍历每个特征向量的第 n 个特征，然后进行非重复计数。如果非重复计数的值是 K ，那么就把这个特征转换为只有一个值是1其他值都是0的 K 维向量。增加下面几行代码到前面的 Python 文件中：

    encoder = preprocessing.OneHotEncoder()    encoder.fit([[0, 2, 1, 12], [1, 3, 5, 3], [2, 3, 2, 12], [1, 2, 4, 3]])    encoded_vector = encoder.transform([[2, 3, 5, 3]]).toarray()    print "\nEncoded vector =", encoded_vector

结果如下所示：

    Encoded vector:    [[ 0.  0.  1.  0.  1.  0.  0.  0.  1.  1.  0.]]

在上面的示例中，观察一下每个特征向量的第三个特征，分别是1、5、2、4这4个不重复的值，也就是说独热编码向量的长度是4。如果你需要对5进行编码，那么向量就是[0, 1, 0, 0]。向量中只有一个值是1。第二个元素是1，对应的值是5。

1.3　标记编码方法

在监督学习中，经常需要处理各种各样的标记。这些标记可能是数字，也可能是单词。如果标记是数字，那么算法可以直接使用它们，但是，许多情况下，标记都需要以人们可理解的形式存在，因此，人们通常会用单词标记训练数据集。标记编码就是要把单词标记转换成数值形式，让算法懂得如何操作标记。接下来看看如何标记编码。

详细步骤

(1) 新建一个 Python 文件，然后导入 preprocessing 程序包：

from sklearn import preprocessing

(2) 这个程序包包含许多数据预处理需要的函数。定义一个标记编码器（label encoder），代码如下所示：

label_encoder = preprocessing.LabelEncoder()

(3) label_encoder对象知道如何理解单词标记。接下来创建一些标记：

input_classes = ['audi', 'ford', 'audi', 'toyota', 'ford', 'bmw']

(4) 现在就可以为这些标记编码了：

label_encoder.fit(input_classes)print "\nClass mapping:"for i, item in enumerate(label_encoder.classes_):    print item, '-->', i

(5) 运行代码，命令行工具中显示下面的结果：

Class mapping:audi --> 0bmw --> 1ford --> 2toyota --> 3

(6) 就像前面结果显示的那样，单词被转换成从0开始的索引值。现在，如果你遇到一组标记，就可以非常轻松地转换它们了，如下所示：

labels = ['toyota', 'ford', 'audi']encoded_labels = label_encoder.transform(labels)print "\nLabels =", labelsprint "Encoded labels =", list(encoded_labels)

命令行工具中将显示下面的结果：

Labels = ['toyota', 'ford', 'audi']Encoded labels = [3, 2, 0]

(7) 这种方式比纯手工进行单词与数字的编码要简单许多。还可以通过数字反转回单词的功能检查结果的正确性：

encoded_labels = [2, 1, 0, 3, 1]decoded_labels = label_encoder.inverse_transform(encoded_labels)print "\nEncoded labels =", encoded_labelsprint "Decoded labels =", list(decoded_labels)

结果如下所示：

Encoded labels = [2, 1, 0, 3, 1]Decoded labels = ['ford', 'bmw', 'audi', 'toyota', 'bmw']

可以看到，映射结果是完全正确的。

第01章：监督学习（中）

1.4　创建线性回归器

回归是估计输入数据与连续值输出数据之间关系的过程。数据通常是实数形式的，我们的目标是估计满足输入到输出映射关系的基本函数。让我们从一个简单的示例开始。考虑下面的输入与输出映射关系：

1 → 2

3 → 6

4.3 → 8.6

7.1 → 14.2

如果要你估计输入与输出的关联关系，你可以通过模式匹配轻松地找到结果。我们发现输出结果一直是输入数据的两倍，因此输入与输出的转换公式就是这样：

f(x) = 2x

这是体现输入值与输出值关联关系的一个简单函数。但是，在真实世界中通常都不会这么简单，输入与输出的映射关系函数并不是一眼就可以看出来的。

1.4.1　准备工作

线性回归用输入变量的线性组合来估计基本函数。前面的示例就是一种单输入单输出变量的线性回归。

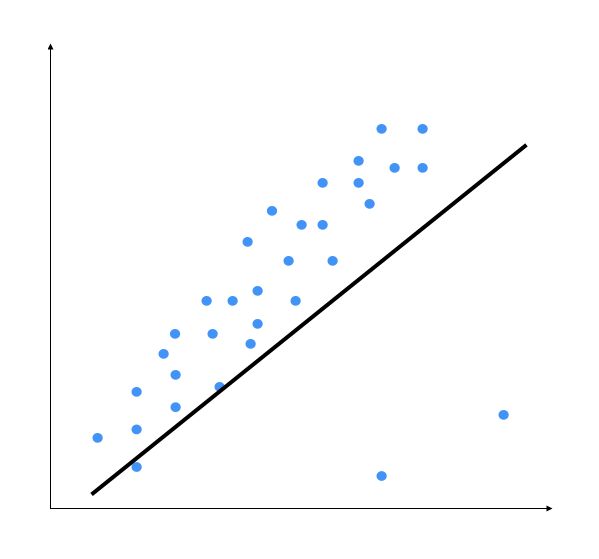
现在考虑如图1-1所示的情况。

图　1-1

线性回归的目标是提取输入变量与输出变量的关联线性模型，这就要求实际输出与线性方程预测的输出的残差平方和（sum of squares of differences）最小化。这种方法被称为普通最小二乘法（Ordinary Least Squares，OLS）。

你可能觉得用一条曲线对这些点进行拟合效果会更好，但是线性回归不允许这样做。线性回归的主要优点就是方程简单。如果你想用非线性回归，可能会得到更准确的模型，但是拟合速度会慢很多。线性回归模型就像前面那张图里显示的，用一条直线近似数据点的趋势。接下来看看如何用 Python 建立线性回归模型。

1.4.2　详细步骤

假设你已经创建了数据文件 data_singlevar.txt，文件里用逗号分隔符分割字段，第一个字段是输入值，第二个字段是与逗号前面的输入值相对应的输出值。你可以用这个文件作为输入参数。

(1) 创建一个 Python 文件 regressor.py，然后在里面增加下面几行代码：

import sysimport numpy as npfilename = sys.argv[1]X = []y = []with open(filename, 'r') as f:    for line in f.readlines():        xt, yt = [float(i) for i in line.split(',')]        X.append(xt)        y.append(yt)

把输入数据加载到变量X和y，其中X是数据，y是标记。在代码的for循环体中，我们解析每行数据，用逗号分割字段。然后，把字段转化为浮点数，并分别保存到变量X和y中。

(2) 建立机器学习模型时，需要用一种方法来验证模型，检查模型是否达到一定的满意度（satisfactory level）。为了实现这个方法，把数据分成两组：训练数据集（training dataset）与测试数据集（testing dataset）。训练数据集用来建立模型，测试数据集用来验证模型对未知数据的学习效果。因此，先把数据分成训练数据集与测试数据集：

num_training = int(0.8 * len(X))num_test = len(X) - num_training# 训练数据X_train = np.array(X[:num_training]).reshape((num_training,1))y_train = np.array(y[:num_training])# 测试数据X_test = np.array(X[num_training:]).reshape((num_test,1))y_test = np.array(y[num_training:])

这里用80%的数据作为训练数据集，其余20%的数据作为测试数据集。

(3) 现在已经准备好训练模型。接下来创建一个回归器对象，代码如下所示：

from sklearn import linear_model# 创建线性回归对象linear_regressor = linear_model.LinearRegression()# 用训练数据集训练模型linear_regressor.fit(X_train, y_train)

(4) 我们利用训练数据集训练了线性回归器。向fit方法提供输入数据即可训练模型。用下面的代码看看它如何拟合：

import matplotlib.pyplot as plty_train_pred = linear_regressor.predict(X_train)plt.figure()plt.scatter(X_train, y_train, color='green')plt.plot(X_train, y_train_pred, color='black', linewidth=4)plt.title('Training data')plt.show()

(5) 在命令行工具中执行如下命令：

$ python regressor.py data_singlevar.txt

就会看到如图1-2所示的线性回归。

图　1-2

(6) 在前面的代码中，我们用训练的模型预测了训练数据的输出结果，但这并不能说明模型对未知的数据也适用，因为我们只是在训练数据上运行模型。这只能体现模型对训练数据的拟合效果。从图1-2中可以看到，模型训练的效果很好。

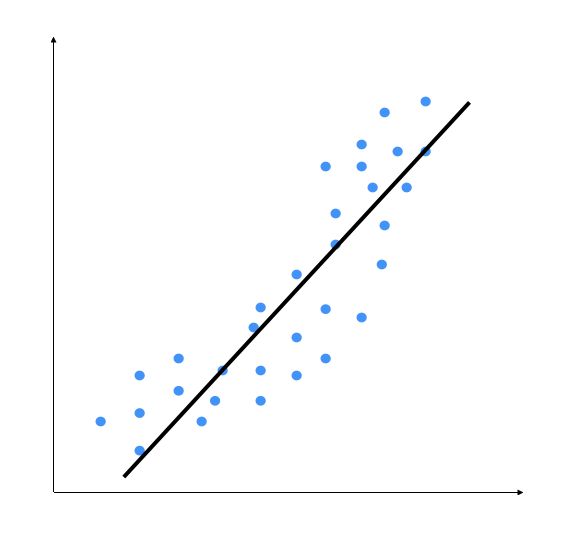
(7) 接下来用模型对测试数据集进行预测，然后画出来看看，代码如下所示：

y_test_pred = linear_regressor.predict(X_test)plt.scatter(X_test, y_test, color='green')plt.plot(X_test, y_test_pred, color='black', linewidth=4)plt.title('Test data')plt.show()

运行代码，可以看到如图1-3所示的线性回归。

图　1-3

1.5　计算回归准确性

现在已经建立了回归器，接下来最重要的就是如何评价回归器的拟合效果。在模型评价的相关内容中，用误差（error）表示实际值与模型预测值之间的差值。

1.5.1　准备工作

下面快速了解几个衡量回归器拟合效果的重要指标（metric）。回归器可以用许多不同的指标进行衡量，部分指标如下所示。

• 平均绝对误差（mean absolute error）：这是给定数据集的所有数据点的绝对误差平均值。

• 均方误差（mean squared error）：这是给定数据集的所有数据点的误差的平方的平均值。这是最流行的指标之一。

• 中位数绝对误差（median absolute error）：这是给定数据集的所有数据点的误差的中位数。这个指标的主要优点是可以消除异常值（outlier）的干扰。测试数据集中的单个坏点不会影响整个误差指标，均值误差指标会受到异常点的影响。

• 解释方差分（explained variance score）：这个分数用于衡量我们的模型对数据集波动的解释能力。如果得分1.0分，那么表明我们的模型是完美的。

• R方得分（R2 score）：这个指标读作“R方”，是指确定性相关系数，用于衡量模型对未知样本预测的效果。最好的得分是1.0，值也可以是负数。

1.5.2　详细步骤

scikit-learn 里面有一个模块，提供了计算所有指标的功能。重新打开一个 Python 文件，然后输入以下代码：

import sklearn.metrics as smprint "Mean absolute error =", round(sm.mean_absolute_error(y_test, y_test_pred), 2)print "Mean squared error =", round(sm.mean_squared_error(y_test, y_ test_pred), 2)print "Median absolute error =", round(sm.median_absolute_error(y_ test, y_test_pred), 2)print "Explained variance score =", round(sm.explained_variance_ score(y_test, y_test_pred), 2)print "R2 score =", round(sm.r2_score(y_test, y_test_pred), 2)

每个指标都描述得面面俱到是非常乏味的，因此只选择一两个指标来评估我们的模型。通常的做法是尽量保证均方误差最低，而且解释方差分最高。

1.6　保存模型数据

模型训练结束之后，如果能够把模型保存成文件，那么下次再使用的时候，只要简单地加载就可以了。

详细步骤

用程序保存模型的具体操作步骤如下。

(1) 在 Python 文件 regressor.py 中加入以下代码：

import cPickle as pickleoutput_model_file = 'saved_model.pkl'with open(output_model_file, 'w') as f:    pickle.dump(linear_regressor, f)

(2) 回归模型会保存在 saved_model.pkl 文件中。下面看看如何加载并使用它，代码如下所示：

with open(output_model_file, 'r') as f:    model_linregr = pickle.load(f)y_test_pred_new = model_linregr.predict(X_test)print "\nNew mean absolute error =", round(sm.mean_absolute_ error(y_test, y_test_pred_new), 2)

(3) 这里只是把回归模型从 Pickle 文件加载到model_linregr变量中。你可以将打印结果与前面的结果进行对比，确认模型与之前的一样。

1.7　创建岭回归器

线性回归的主要问题是对异常值敏感。在真实世界的数据收集过程中，经常会遇到错误的度量结果。而线性回归使用的普通最小二乘法，其目标是使平方误差最小化。这时，由于异常值误差的绝对值很大，因此会引起问题，从而破坏整个模型。

1.7.1　准备工作

先看图1-4。

图　1-4

右下角的两个数据点明显是异常值，但是这个模型需要拟合所有的数据点，因此导致整个模型都错了。仅凭直觉观察，我们就会觉得如图1-5的拟合结果更好。

图　1-5

普通最小二乘法在建模时会考虑每个数据点的影响，因此，最终模型就会像图1-4显示的直线那样。显然，我们发现这个模型不是最优的。为了避免这个问题，我们引入正则化项的系数作为阈值来消除异常值的影响。这个方法被称为岭回归。

1.7.2　详细步骤

接下来看看如何用 Python 建立岭回归器。

(1) 你可以从 data_multi_variable.txt 文件中加载数据。这个文件的每一行都包含多个数值。除了最后一个数值外，前面的所有数值构成输入特征向量。

(2) 把下面的代码加入 regressor.py 文件中。我们用一些参数初始化岭回归器：

ridge_regressor = linear_model.Ridge(alpha=0.01, fit_ intercept=True, max_iter=10000)

(3) alpha参数控制回归器的复杂程度。当alpha趋于0时，岭回归器就是用普通最小二乘法的线性回归器。因此，如果你希望模型对异常值不那么敏感，就需要设置一个较大的alpha值。这里把alpha值设置为0.01。

(4) 下面让我们来训练岭回归器。

ridge_regressor.fit(X_train, y_train)y_test_pred_ridge = ridge_regressor.predict(X_test)print "Mean absolute error =", round(sm.mean_absolute_error    (y_ test, y_test_pred_ridge), 2)print "Mean squared error =", round(sm.mean_squared_error    (y_test, y_test_pred_ridge), 2)print "Median absolute error =", round(sm.median_absolute_error    (y_ test, y_test_pred_ridge), 2)print "Explain variance score =", round(sm.explained_variance_ score    (y_test, y_test_pred_ridge), 2)print "R2 score =", round(sm.r2_score(y_test, y_test_pred_ridge), 2)

运行代码检查误差指标。可以用同样的数据建立一个线性回归器，并与岭回归器的结果进行比较，看看把正则化引入回归模型之后的效果如何。

第01章：监督学习（下）

1.8　创建多项式回归器

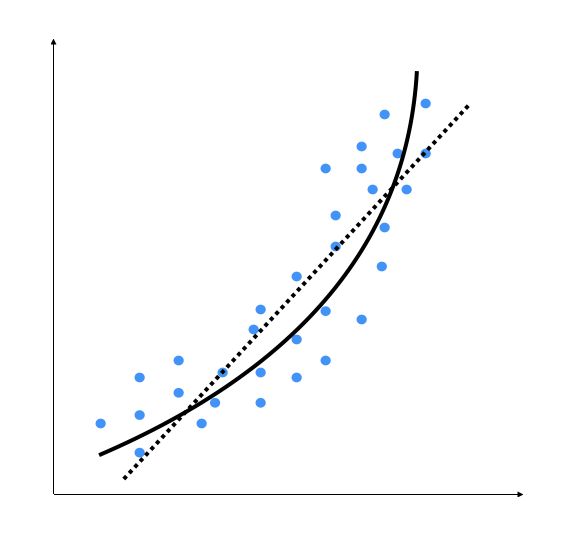
线性回归模型有一个主要的局限性，那就是它只能把输入数据拟合成直线，而多项式回归模型通过拟合多项式方程来克服这类问题，从而提高模型的准确性。

1.8.1　准备工作

先看图1-6。

图　1-6

从图1-6中可以看到，数据点本身的模式中带有自然的曲线，而线性模型是不能捕捉到这一点的。再来看看多项式模型的效果，如图1-7所示。

图　1-7

图1-7中的虚线表示线性回归模型，实线表示多项式回归模型。这个模型的曲率是由多项式的次数决定的。随着模型曲率的增加，模型变得更准确。但是，增加曲率的同时也增加了模型的复杂性，因此拟合速度会变慢。当我们对模型的准确性的理想追求与计算能力限制的残酷现实发生冲突时，就需要综合考虑了。

1.8.2　详细步骤

(1) 将下面的代码加入 Python 文件 regressor.py 中：

from sklearn.preprocessing import PolynomialFeaturespolynomial = PolynomialFeatures(degree=3)

(2) 上一行将曲线的多项式的次数的初始值设置为3。下面用数据点来计算多项式的参数：

X_train_transformed = polynomial.fit_transform(X_train)

其中，X_train_transformed表示多项式形式的输入，与线性回归模型是一样大的。

(3) 接下来用文件中的第一个数据点来检查多项式模型是否能够准确预测：

datapoint = [0.39,2.78,7.11]poly_datapoint = polynomial.fit_transform(datapoint)poly_linear_model = linear_model.LinearRegression()poly_linear_model.fit(X_train_transformed, y_train)print "\nLinear regression:", linear_regressor.predict(datapoint) [0]print "\nPolynomial regression:", poly_linear_model.predict(poly_datapoint)[0]

多项式回归模型计算变量数据点的值恰好就是输入数据文件中的第一行数据值。再用线性回归模型测试一下，唯一的差别就是展示数据的形式。运行代码，可以看到下面的结果：

Linear regression: -11.0587294983Polynomial regression: -10.9480782122

可以发现，多项式回归模型的预测值更接近实际的输出值。如果想要数据更接近实际输出值，就需要增加多项式的次数。

(4) 将多项式的次数加到10看看结果：

polynomial = PolynomialFeatures(degree=10)

可以看到下面的结果：

Polynomial regression: -8.20472183853

现在，你可以发现预测值与实际的输出值非常地接近。

1.9　估算房屋价格

是时候用所学的知识来解决真实世界的问题了。让我们用这些原理来估算房屋价格。房屋估价是理解回归分析最经典的案例之一，通常是一个不错的切入点。它符合人们的直觉，而且与人们的生活息息相关，因此在用机器学习处理复杂事情之前，通过房屋估价可以更轻松地理解相关概念。我们将使用带 AdaBoost 算法的决策树回归器（decision tree regressor）来解决这个问题。

1.9.1　准备工作

决策树是一个树状模型，每个节点都做出一个决策，从而影响最终结果。叶子节点表示输出数值，分支表示根据输入特征做出的中间决策。AdaBoost 算法是指自适应增强（adaptive boosting）算法，这是一种利用其他系统增强模型准确性的技术。这种技术是将不同版本的算法结果进行组合，用加权汇总的方式获得最终结果，被称为弱学习器（weak learners）。AdaBoost 算法在每个阶段获取的信息都会反馈到模型中，这样学习器就可以在后一阶段重点训练难以分类的样本。这种学习方式可以增强系统的准确性。

首先使用 AdaBoost 算法对数据集进行回归拟合，再计算误差，然后根据误差评估结果，用同样的数据集重新拟合。可以把这些看作是回归器的调优过程，直到达到预期的准确性。假设你拥有一个包含影响房价的各种参数的数据集，我们的目标就是估计这些参数与房价的关系，这样就可以根据未知参数估计房价了。

1.9.2　详细步骤

(1) 创建一个新的 Python 文件 housing.py，然后加入下面的代码：

import numpy as npfrom sklearn.tree import DecisionTreeRegressorfrom sklearn.ensemble import AdaBoostRegressorfrom sklearn import datasetsfrom sklearn.metrics import mean_squared_error, explained_variance_scorefrom sklearn.utils import shuffleimport matplotlib.pyplot as plt

(2) 网上有一个标准房屋价格数据库，人们经常用它来研究机器学习。你可以在这里下载数据。不过 scikit-learn 提供了数据接口，可以直接通过下面的代码加载数据：

housing_data = datasets.load_boston()

每个数据点由影响房价的13个输入参数构成。你可以用housing_data.data获取输入的数据，用housing_data.target获取对应的房屋价格。

(3) 接下来把输入数据与输出结果分成不同的变量。我们可以通过shuffle函数把数据的顺序打乱：

X, y = shuffle(housing_data.data, housing_data.target, random_ state=7)

(4) 参数random_state用来控制如何打乱数据，让我们可以重新生成结果。接下来把数据分成训练数据集和测试数据集，其中80%的数据用于训练，剩余20%的数据用于测试：

num_training = int(0.8 * len(X))X_train, y_train = X[:num_training], y[:num_training]X_test, y_test = X[num_training:], y[num_training:]

(5) 现在已经可以拟合一个决策树回归模型了。选一个最大深度为4的决策树，这样可以限制决策树不变成任意深度：

dt_regressor = DecisionTreeRegressor(max_depth=4)dt_regressor.fit(X_train, y_train)

(6) 再用带 AdaBoost 算法的决策树回归模型进行拟合：

ab_regressor =AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=400, random_state=7)ab_regressor.fit(X_train, y_train)

这样可以帮助我们对比训练效果，看看 AdaBoost 算法对决策树回归器的训练效果有多大改善。

(7) 接下来评价决策树回归器的训练效果：

y_pred_dt = dt_regressor.predict(X_test)mse = mean_squared_error(y_test, y_pred_dt)evs = explained_variance_score(y_test, y_pred_dt)print "\n#### Decision Tree performance ####"print "Mean squared error =", round(mse, 2)print "Explained variance score =", round(evs, 2)

(8) 现在评价一下 AdaBoost 算法改善的效果：

y_pred_ab = ab_regressor.predict(X_test)mse = mean_squared_error(y_test, y_pred_ab)evs = explained_variance_score(y_test, y_pred_ab)print "\n#### AdaBoost performance ####"print "Mean squared error =", round(mse, 2)print "Explained variance score =", round(evs, 2)

(9) 命令行工具显示的输出结果如下所示：

#### 决策树学习效果 ####Mean squared error = 14.79Explained variance score = 0.82#### AdaBoost算法改善效果 ####Mean squared error = 7.54Explained variance score = 0.91

前面的结果表明，AdaBoost 算法可以让误差更小，且解释方差分更接近1。

1.10　计算特征的相对重要性

所有特征都同等重要吗？在这个案例中，我们用了13个特征，它们对模型都有贡献。但是，有一个重要的问题出现了：如何判断哪个特征更加重要？显然，所有的特征对结果的贡献是不一样的。如果需要忽略一些特征，就需要知道哪些特征不太重要。scikit-learn 里面有这样的功能。

详细步骤

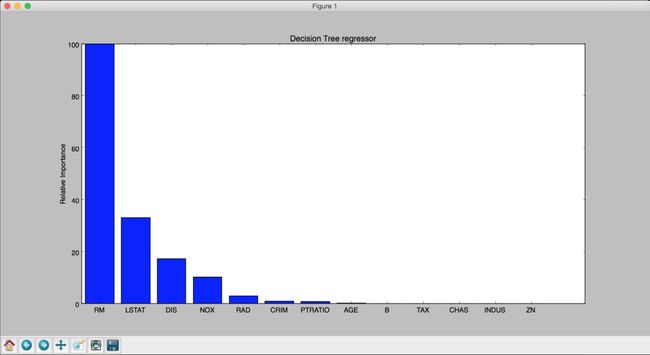
(1) 画出特征的相对重要性，在 housing.py 文件中加入下面几行代码：

plot_feature_importances(dt_regressor.feature_importances_,        'Decision Tree regressor', housing_data.feature_names)plot_feature_importances(ab_regressor.feature_importances_,        'AdaBoost regressor', housing_data.feature_names)

回归器对象有一个feature_importances_方法会告诉我们每个特征的相对重要性。

(2) 接下来需要定义plot_feature_importances来画出条形图：

def plot_feature_importances(feature_importances, title, feature_names):    # 将重要性值标准化    feature_importances = 100.0 * (feature_importances / max(feature_importances))    # 将得分从高到低排序    index_sorted = np.flipud(np.argsort(feature_importances))    # 让X坐标轴上的标签居中显示    pos = np.arange(index_sorted.shape[0]) + 0.5    # 画条形图    plt.figure()    plt.bar(pos, feature_importances[index_sorted], align='center')    plt.xticks(pos, feature_names[index_sorted])    plt.ylabel('Relative Importance')    plt.title(title)    plt.show()

(3) 我们从feature_importances_方法里取值，然后把数值放大到0~100的范围内。运行前面的代码，可以看到两张图（不带 AdaBoost 算法与带 AdaBoost 算法两种模型）。仔细观察图1-8和图1-9，看看能从决策树回归器中获得什么。

图　1-8

(4) 从图1-8可以发现，不带 AdaBoost 算法的决策树回归器显示的最重要特征是 RM。再看看带 AdaBoost 算法的决策树回归器的特征重要性排序条形图，如图1-9所示。

图　1-9

加入 AdaBoost 算法之后，房屋估价模型的最重要特征是 LSTAT。在现实生活中，如果对这个数据集建立不同的回归器，就会发现最重要的特征是 LSTAT，这足以体现 AdaBoost 算法对决策树回归器训练效果的改善。

1.11　评估共享单车的需求分布

本节将用一种新的回归方法解决共享单车的需求分布问题。我们采用随机森林回归器（random forest regressor）估计输出结果。随机森林是一个决策树集合，它基本上就是用一组由数据集的若干子集构建的决策树构成，再用决策树平均值改善整体学习效果。

1.11.1　准备工作

我们将使用 bike_day.csv 文件中的数据集获取。这份数据集一共16列，前两列是序列号与日期，分析的时候可以不用；最后三列数据是不同类型的输出结果；最后一列是第十四列与第十五列的和，因此建立模型时可以不考虑第十四列与第十五列。

1.11.2　详细步骤

接下来看看 Python 如何解决这个问题。如果你下载了本书源代码，就可以看到 bike_sharing.py 文件里已经包含了完整代码。这里将介绍若干重要的部分。

(1) 首先导入一些新的程序包，如下：

import csvfrom sklearn.ensemble import RandomForestRegressorfrom housing import plot_feature_importances

(2) 我们需要处理 CSV 文件，因此加入了 csv 程序包来读取 CSV 文件。由于这是一个全新的数据集，因此需要自己定义一个数据集加载函数：

def load_dataset(filename):    file_reader = csv.reader(open(filename, 'rb'), delimiter=',')    X, y = [], []    for row in file_reader:        X.append(row[2:13])        y.append(row[-1])    # 提取特征名称    feature_names = np.array(X[0])    # 将第一行特征名称移除，仅保留数值    return np.array(X[1:]).astype(np.float32), np.array(y[1:]).astype(np.float32), feature_names

在这个函数中，我们从 CSV 文件读取了所有数据。把数据显示在图形中时，特征名称非常有用。把特征名称数据从输入数值中分离出来，并作为函数返回值。

(3) 读取数据，并打乱数据顺序，让新数据与原来文件中数据排列的顺序没有关联性：

X, y, feature_names = load_dataset(sys.argv[1])X, y = shuffle(X, y, random_state=7)

(4) 和之前的做法一样，需要将数据分成训练数据和测试数据。这一次，我们将90%的数据用于训练，剩余10%的数据用于测试：

num_training = int(0.9 * len(X))X_train, y_train = X[:num_training], y[:num_training]X_test, y_test = X[num_training:], y[num_training:]

(5) 下面开始训练回归器：

rf_regressor = RandomForestRegressor(n_estimators=1000, max_depth=10, min_samples_split=1)rf_regressor.fit(X_train, y_train)

其中，参数n_estimators是指评估器（estimator）的数量，表示随机森林需要使用的决策树数量；参数max_depth是指每个决策树的最大深度；参数min_samples_split是指决策树分裂一个节点需要用到的最小数据样本量。

(6) 评价随机森林回归器的训练效果：

y_pred = rf_regressor.predict(X_test)mse = mean_squared_error(y_test, y_pred)evs = explained_variance_score(y_test, y_pred)print "\n#### Random Forest regressor performance ####"print "Mean squared error =", round(mse, 2)print "Explained variance score =", round(evs, 2)

(7) 由于已经有画出特征重要性条形图的函数plot_feature_importances了，接下来直接调用它：

plot_feature_importances(rf_regressor.feature_importances_, 'Random Forest regressor', feature_names)

执行代码，可以看到如图1-10所示的图形。

图　1-10

看来温度（temp）是影响自行车租赁的最重要因素。

1.11.3　更多内容

把第十四列与第十五列数据加入数据集，看看结果有什么区别。在新的特征重要性条形图中，除了这两个特征外，其他特征都变成了0。这是由于输出结果可以通过简单地对第十四列与第十五列数据求和得出，因此算法不需要其他特征计算结果。在数据集加载函数load_dataset中，我们需要对for循环内的取值范围稍作调整：

X.append(row[2:15])

现在再画出特征重要性条形图，可以看到如图1-11所示的柱形图。

图　1-11

与预想的一样，从图中可以看出，只有这两个特征是重要的，这确实也符合常理，因为最终结果仅仅是这两个特征相加得到的。因此，这两个变量与输出结果有直接的关系，回归器也就认为它不需要其他特征来预测结果了。在消除数据集冗余变量方面，这是非常有用的工具。

还有一份按小时统计的自行车共享数据 bike_hour.csv。我们需要用到第3~14列，因此先对数据集加载函数load_dataset做一点调整：

X.append(row[2:14])

运行代码，可以看到回归器的训练结果如下：

#### 随机森林学习效果 ####Mean squared error = 2619.87Explained variance score = 0.92

特征重要性条形图如图1-12所示。

图　1-12

图1-12中显示，最重要的特征是一天中的不同时点（hr），这也完全符合人们的直觉；其次重要的是温度，与我们之前分析的结果一致。

第02章：创建分类器（上）

在这一章，我们将介绍以下主题：

• 建立简单分类器（simple classifier）

• 建立逻辑回归分类器（logistic regression classifier）

• 建立朴素贝叶斯分类器（Naïve Bayes classifier）

• 将数据集分割成训练集和测试集

• 用交叉验证（cross-validation）检验模型准确性

• 混淆矩阵（confusion matrix）可视化

• 提取性能报告

• 根据汽车特征评估质量

• 生成验证曲线（validation curves）

• 生成学习曲线（learning curves）

• 估算收入阶层（income bracket）

2.1　简介

在机器学习领域中，分类是指利用数据的特性将其分成若干类型的过程。分类与上一章介绍的回归不同，回归的输出结果是实数。监督学习分类器就是用带标记的训练数据建立一个模型，然后对未知数据进行分类。

分类器可以是实现分类功能的任意算法，最简单的分类器就是简单的数学函数。在真实世界中，分类器可以是非常复杂的形式。在学习过程中，可以看到二元（binary）分类器，将数据分成两类，也可以看到多元（multiclass）分类器，将数据分成两个以上的类型。解决分类问题的数据手段都倾向于解决二元分类问题，可以通过不同的形式对其进行扩展，进而解决多元分类问题。

分类器准确性的估计是机器学习领域的重要内容。我们需要学会如何使用现有的数据获取新的思路（机器学习模型），然后把模型应用到真实世界中。在这一章里，我们将看到许多类似的主题。

2.2　建立简单分类器

本节学习如何用训练数据建立一个简单分类器。

2.2.1　详细步骤

(1)使用 simple_classifier.py 文件作为参考。假设你已经和上一章一样导入了numpy和matplotlib.pyplot程序包，那么需要创建一些样本数据：

X = np.array([[3,1], [2,5], [1,8], [6,4], [5,2], [3,5], [4,7], [4,-1]])

(2) 为这些数据点分配一些标记：

y = [0, 1, 1, 0, 0, 1, 1, 0]

(3) 因为只有两个类，所以y列表包含0和1。一般情况下，如果你有 N个类，那么y的取值范围就是从0到 N-1。接下来按照类型标记把样本数据分成两类：

class_0 = np.array([X[i] for i in range(len(X)) if y[i]==0])class_1 = np.array([X[i] for i in range(len(X)) if y[i]==1])

(4) 为了对数据有个直观的认识，把图像画出来，如下所示：

plt.figure()plt.scatter(class_0[:,0], class_0[:,1], color='black', marker='s')plt.scatter(class_1[:,0], class_1[:,1], color='black', marker='x')

这是一个散点图（scatterplot），用方块和叉表示两类数据。在前面的代码中，参数marker用来表示数据点的形状。用方块表示class_0的数据，用叉表示class_1的数据。运行代码，可以看到如图2-1所示的图形。

(5) 在之前的两行代码中，只是用变量X与y之间的映射关系创建了两个列表。如果要你直观地展示数据点的不同类型，在两类数据间画一条分割线，那么怎么实现呢？你只要用直线方程在两类数据之间画一条直线就可以了。下面看看如何实现：

line_x = range(10)line_y = line_x

(6) 用数学公式 y = x 创建一条直线。代码如下所示：

plt.figure()plt.scatter(class_0[:,0], class_0[:,1], color='black', marker='s')plt.scatter(class_1[:,0], class_1[:,1], color='black', marker='x')plt.plot(line_x, line_y, color='black', linewidth=3)plt.show()

图　2-1

(7) 运行代码，可以看到如图2-2所示的图形。

图　2-2

2.2.2　更多内容

用以下规则建立了一个简单的分类器：如果输入点(a, b)的a大于或等于b，那么它属于类型class_0；反之，它属于class_1。如果对数据点逐个进行检查，你会发现每个数都是这样，这样你就建立了一个可以识别未知数据的线性分类器（linear classifier）。之所以称其为线性分类器，是因为分割线是一条直线。如果分割线是一条曲线，就是非线性分类器（nonlinear classifier）。

这样简单的分类器之所以可行，是因为数据点很少，可以直观地判断分割线。如果有几千个数据点呢？如何对分类过程进行一般化处理（generalize）呢？下一节将介绍这一主题。

2.3　建立逻辑回归分类器

虽然这里也出现了上一章介绍的回归这个词，但逻辑回归其实是一种分类方法。给定一组数据点，需要建立一个可以在类之间绘制线性边界的模型。逻辑回归就可以对训练数据派生的一组方程进行求解来提取边界。

详细步骤

(1) 下面看看用 Python 如何实现逻辑回归。我们使用 logistic_regression.py 文件作为参考。假设已经导入了需要使用的程序包，接下来创建一些带训练标记的样本数据：

import numpy as npfrom sklearn import linear_modelimport matplotlib.pyplot as pltX = np.array([[4, 7], [3.5, 8], [3.1, 6.2], [0.5, 1], [1, 2],[1.2, 1.9], [6, 2], [5.7, 1.5], [5.4, 2.2]])y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2])

这里假设一共有3个类。

(2) 初始化一个逻辑回归分类器：

classifier = linear_model.LogisticRegression(solver='liblinear', C=100)

前面的函数有一些输入参数需要设置，但是最重要的两个参数是solver和C。参数solver用于设置求解系统方程的算法类型，参数C表示正则化强度，数值越小，表示正则化强度越高。

(3) 接下来训练分类器：

classifier.fit(X, y)

(4) 画出数据点和边界：

plot_classifier(classifier, X, y)

需要定义如下画图函数：

def plot_classifier(classifier, X, y):    # 定义图形的取值范围    x_min, x_max = min(X[:, 0]) - 1.0, max(X[:, 0]) + 1.0    y_min, y_max = min(X[:, 1]) - 1.0, max(X[:, 1]) + 1.0

预测值表示我们在图形中想要使用的数值范围，通常是从最小值到最大值。我们增加了一些余量（buffer），例如上面代码中的1.0。

(5) 为了画出边界，还需要利用一组网格（grid）数据求出方程的值，然后把边界画出来。下面继续定义网格：

    # 设置网格数据的步长    step_size = 0.01    # 定义网格    x_values, y_values = np.meshgrid(np.arange(x_min, x_max, step_size), np.arange(y_min, y_max, step_size))

变量x_values和y_values包含求解方程数值的网格点。

(6) 计算出分类器对所有数据点的分类结果：

    # 计算分类器输出结果    mesh_output = classifier.predict(np.c_[x_values.ravel(), y_values.ravel()])    # 数组维度变形    mesh_output = mesh_output.reshape(x_values.shape)

(7) 用彩色区域画出各个类型的边界：

    # 用彩图画出分类结果    plt.figure()    # 选择配色方案    plt.pcolormesh(x_values, y_values, mesh_output, cmap=plt.cm.gray)

这基本算是一个三维画图器，既可以画二维数据点，又可以用色彩清单（color scheme）表示不同区域的相关属性。你可以在这里找到所有的色彩清单。

(8) 接下来再把训练数据点画在图上：

    plt.scatter(X[:, 0], X[:, 1], c=y, s=80, edgecolors='black', linewidth=1, cmap=plt.cm.Paired)    # 设置图形的取值范围    plt.xlim(x_values.min(), x_values.max())    plt.ylim(y_values.min(), y_values.max())    # 设置X轴与Y轴    plt.xticks((np.arange(int(min(X[:, 0])-1), int(max(X[:, 0])+1), 1.0)))    plt.yticks((np.arange(int(min(X[:, 1])-1), int(max(X[:, 1])+1), 1.0)))    plt.show()

其中，plt.scatter把数据点画在二维图上。X[:, 0]表示0轴（X轴）的坐标值，X[:, 1]表示1轴（Y轴）的坐标值。c=y表示颜色的使用顺序。用目标标记映射cmap的颜色表。我们肯定希望不同的标记使用不同的颜色，因此，用y作为映射。坐标轴的取值范围由plt.xlim和plt.ylim确定。为了标记坐标轴的数值，需要使用plt.xticks和plt.yticks。在坐标轴上标出坐标值，就可以直观地看出数据点的位置。在前面的代码中，我们希望坐标轴的最大值与最小值之前的刻度是单位刻度，还希望这些刻度值是整数，因此用int()函数对最值取整。

(9) 运行代码，就可以看到如图2-3所示的输出结果。

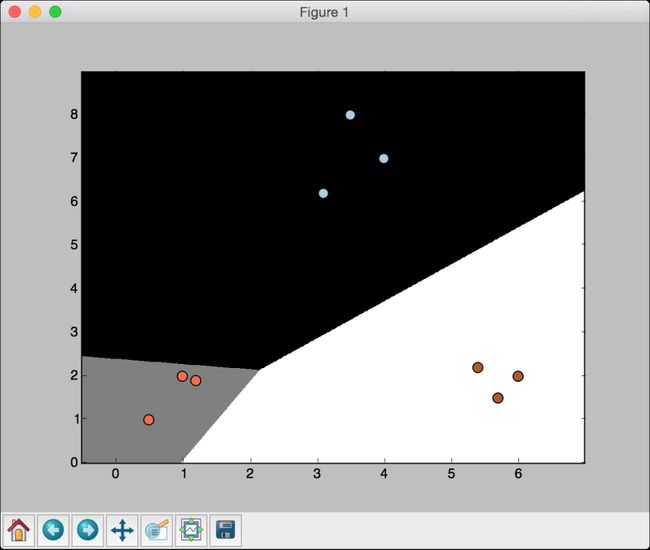
图　2-3

(10) 下面看看参数C对模型的影响。参数C表示对分类错误（misclassification）的惩罚值（penalty）。如果把参数C设置为1.0，会得到如图2-4所示的结果。

图　2-4

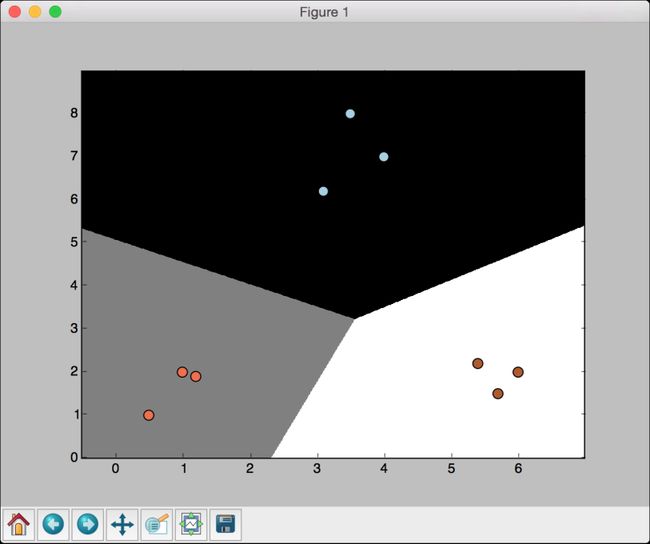
(11) 如果把参数C设置为10000，会得到如图2-5所示的结果。

图　2-5

随着参数C的不断增大，分类错误的惩罚值越高。因此，各个类型的边界更优。

2.4　建立朴素贝叶斯分类器

朴素贝叶斯分类器是用贝叶斯定理进行建模的监督学习分类器。下面看看如何建立一个朴素贝叶斯分类器。

详细步骤

(1) 我们使用naive_bayes.py文件作为参考。首先导入两个程序包：

from sklearn.naive_bayes import GaussianNBfrom logistic_regression import plot_classifier

(2) 下载的示例代码中有一个data_multivar.txt文件，里面包含了将要使用的数据，每一行数据都是由逗号分隔符分割的数值。从文件中加载数据：

input_file = 'data_multivar.txt'X = []y = []with open(input_file, 'r') as f:    for line in f.readlines():        data = [float(x) for x in line.split(',')]        X.append(data[:-1])        y.append(data[-1])X = np.array(X)y = np.array(y)

我们已经把输入数据和标记分别加载到变量X和y中了。

(3) 下面建立一个朴素贝叶斯分类器：

classifier_gaussiannb = GaussianNB()classifier_gaussiannb.fit(X, y)y_pred = classifier_gaussiannb.predict(X)

GaussianNB函数指定了正态分布朴素贝叶斯模型（Gaussian Naive Bayes model）。

(4) 接下来计算分类器的准确性：

accuracy = 100.0 * (y == y_pred).sum() / X.shape[0]print "Accuracy of the classifier =", round(accuracy, 2), "%"

(5) 画出数据点和边界：

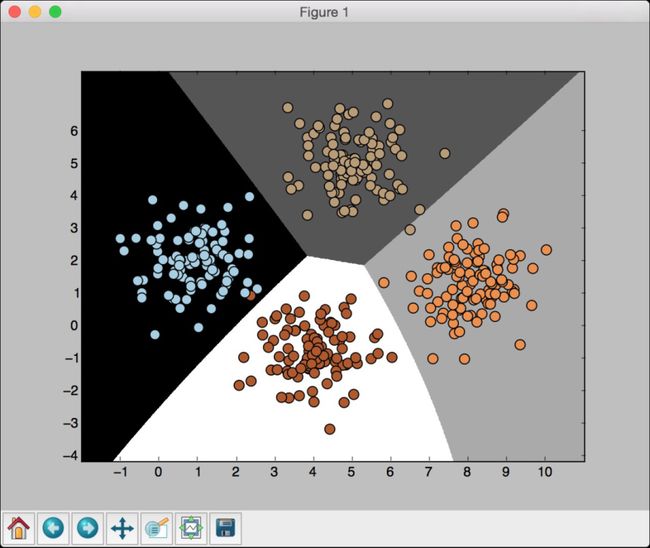
plot_classifier(classifier_gaussiannb, X, y)

可以看到如图2-6所示的图形。

图　2-6

从图2-6中可以发现，这里的边界没有严格地区分所有数据点。在前面这个例子中，我们是对所有的数据进行训练。机器学习的一条最佳实践是用没有重叠（nonoverlapping）的数据进行训练和测试。理想情况下，需要一些尚未使用的数据进行测试，可以方便准确地评估模型在未知数据上的执行情况。scikit-learn 有一个方法可以非常好地解决这个问题，我们将在下一节介绍它。

第02章：创建分类器（中）

2.5　将数据集分割成训练集和测试集

本节一起来看看如何将数据合理地分割成训练数据集和测试数据集。

详细步骤

(1) 增加下面的代码片段到上一节的 Python 文件中：

from sklearn import cross_validationX_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.25, random_state=5)classifier_gaussiannb_new = GaussianNB()classifier_gaussiannb_new.fit(X_train, y_train)

这里，我们把参数test_size设置成0.25，表示分配了25%的数据给测试数据集。剩下75%的数据将用于训练数据集。

(2) 用分类器对测试数据进行测试：

y_test_pred = classifier_gaussiannb_new.predict(X_test)

(3) 计算分类器的准确性：

accuracy = 100.0 * (y_test == y_test_pred).sum() / X_test.shape[0]print "Accuracy of the classifier =", round(accuracy, 2), "%"

(4) 画出测试数据的数据点及其边界：

plot_classifier(classifier_gaussiannb_new, X_test, y_test)

(5) 可以看到如图2-7所示的图形。

图　2-7

2.6　用交叉验证检验模型准确性

交叉验证是机器学习的重要概念。在上一节中，我们把数据分成了训练数据集和测试数据集。然而，为了能够让模型更加稳定，还需要用数据集的不同子集进行反复的验证。如果只是对特定的子集进行微调，最终可能会过度拟合（overfitting）模型。过度拟合是指模型在已知数据集上拟合得超级好，但是一遇到未知数据就挂了。我们真正想要的，是让机器学习模型能够适用于未知数据。

2.6.1　准备工作

介绍如何实现交叉验证之前，先讨论一下性能指标。当处理机器学习模型时，通常关心3个指标：精度（precision）、召回率（recall）和F1得分（F1 score）。可以用参数评分标准（parameter scoring）获得各项指标的得分。精度是指被分类器正确分类的样本数量占分类器总分类样本数量的百分比（分类器分类结果中，有一些样本分错了）。召回率是指被应正确分类的样本数量占某分类总样本数量的百分比（有一些样本属于某分类，但分类器却没有分出来）。

假设数据集有100个样本，其中有82个样本是我们感兴趣的，现在想用分类器选出这82个样本。最终，分类器选出了73个样本，它认为都是我们感兴趣的。在这73个样本中，其实只有65个样本是我们感兴趣的，剩下的8个样本我们不感兴趣，是分类器分错了。可以如下方法计算分类器的精度：

• 分类正确的样本数量 = 65

• 总分类样本数量 = 73

• 精度 = 65 / 73 = 89.04%

召回率的计算过程如下：

• 数据集中我们感兴趣的样本数量 = 82

• 分类正确的样本数量 = 65

• 召回率 = 65 / 82 = 79.26%

一个给力的机器学习模型需要同时具备良好的精度和召回率。这两个指标是二律背反的，一个指标达到100%，那么另一个指标就会非常差！我们需要保持两个指标能够同时处于合理高度。为了量化两个指标的均衡性，引入了 F1得分指标，是精度和召回率的合成指标，实际上是精度和召回率的调和均值（harmonic mean）：

F1 得分＝2×精度×召回率 / (精度＋召回率)

上面示例中 F1得分的计算过程如下：

F1 得分＝2×0.89×0.79 / (0.89＋0.79)＝0.8370

2.6.2　详细步骤

(1) 下面看看如何实现交叉验证，并提取性能指标。首先计算精度：

num_validations = 5accuracy = cross_validation.cross_val_score(classifier_gaussiannb,        X, y,scoring='accuracy', cv=num_validations)print "Accuracy: " + str(round(100*accuracy.mean(), 2)) + "%"

(2) 用前面的方程分别计算精度、召回率和F1得分：

f1 = cross_validation.cross_val_score(classifier_gaussiannb,        X, y, scoring='f1_weighted', cv=num_validations)print "F1: " + str(round(100*f1.mean(), 2)) + "%"precision = cross_validation.cross_val_score(classifier_ gaussiannb,        X, y, scoring='precision_weighted', cv=num_validations)print "Precision: " + str(round(100*precision.mean(), 2)) + "%"recall = cross_validation.cross_val_score(classifier_gaussiannb,        X, y, scoring='recall_weighted', cv=num_validations)print "Recall: " + str(round(100*recall.mean(), 2)) + "%"

2.7　混淆矩阵可视化

混淆矩阵（confusion matrix）是理解分类模型性能的数据表，它有助于我们理解如何把测试数据分成不同的类。当想对算法进行调优时，就需要在对算法做出改变之前了解数据的错误分类情况。有些分类效果比其他分类效果更差，混淆矩阵可以帮助我们理解这些问题。先看看如图2-8所示的混淆矩阵。

图　2-8

在图2-8中，我们可以看出不同类型的分类数据。理想情况下，我们希望矩阵非对角线元素都是0，这是最完美的分类结果。先看看class 0，一共52个样本属于class 0。如果对第一行数据求和，总数就是52。但是现在，只有45个样本被正确地预测出来，分类器说另外4个样本属于class 1，还有3个样本属于class 2。用同样的思路分析另外两行数据，有意思的是，class 1里面有11个样本被错误地预测成了class 0，占到了class 1总数的16%。这就是模型需要优化的切入点。

详细步骤

(1) 我们用 confusion_matrix.py 文件作为参考。首先看看如何从数据中提取混淆矩阵：

from sklearn.metrics import confusion_matrixy_true = [1, 0, 0, 2, 1, 0, 3, 3, 3]y_pred = [1, 1, 0, 2, 1, 0, 1, 3, 3]confusion_mat = confusion_matrix(y_true, y_pred)plot_confusion_matrix(confusion_mat)

这里用了一些样本数据，一共有4种类型，取值范围是0~3，也列出了预测的标记类型。用confusion_matrix方法提取混淆矩阵，然后把它画出来。

(2) 继续定义混淆矩阵的画图函数：

# 显示混淆矩阵def plot_confusion_matrix(confusion_mat):    plt.imshow(confusion_mat, interpolation='nearest', cmap=plt.cm.Paired)    plt.title('Confusion matrix')    plt.colorbar()    tick_marks = np.arange(4)    plt.xticks(tick_marks, tick_marks)    plt.yticks(tick_marks, tick_marks)    plt.ylabel('True label')    plt.xlabel('Predicted label')    plt.show()

这里用imshow函数画混淆矩阵，其他函数都非常简单，只使用相关函数设置了图形的标题、颜色栏、刻度和标签。参数tick_marks的取值范围是0~3，因为数据集中有4个标记类型。np.arange函数会生成一个numpy数组。

(3) 运行代码，可以看到如图2-9所示的图形。

图　2-9

从图2-9中可以看出，对角线的颜色很亮，我们希望它们越亮越好。黑色区域表示0。在非对角线的区域有一些灰色区域，表示分类错误的样本量。例如，当样本真实标记类型是0，而预测标记类型是1时，就像在第一行的第二格看到的那样。事实上，所有的错误分类都属于class-1，因为第二列有3个不为0的格子。这在图2-9中显示得一目了然。

2.8　提取性能报告

也可以直接用 scikit-learn 打印精度、召回率和 F1得分。接下来看看如何实现。

详细步骤

(1) 在一个新的 Python 文件中加入下面的代码：

from sklearn.metrics import classification_reporty_true = [1, 0, 0, 2, 1, 0, 3, 3, 3]y_pred = [1, 1, 0, 2, 1, 0, 1, 3, 3]target_names = ['Class-0', 'Class-1', 'Class-2', 'Class-3']print(classification_report(y_true, y_pred, target_names=target_names))

(2) 运行代码，可以在命令行工具中看到如图2-10所示的结果。

图　2-10

不需要单独计算各个指标，可以直接用这个函数从模型中提取所有统计值。

2.9　根据汽车特征评估质量

接下来看看如何用分类技术解决现实问题。我们将用一个包含汽车多种细节的数据集，例如车门数量、后备箱大小、维修成本等，来确定汽车的质量。分类的目的是把车辆的质量分成4种类型：不达标、达标、良好、优秀。

2.9.1　准备工作

你可以从这里下载数据集。

你需要把数据集中的每个值看成是字符串。考虑数据集中的6个属性，其取值范围是这样的：

• buying：取值范围是vhigh、high、med、low；

• maint：取值范围是vhigh、high、med、low；

• doors：取值范围是2、3、4、5等；

• persons：取值范围是2、4等；

• lug_boot：取值范围是small、med、big；

• safety：取值范围是low、med、high。

考虑到每一行都包含字符串属性，需要假设所有特征都是字符串，并设置分类器。在上一章中，我们用随机森林建立过回归器，这里再用随机森林建立分类器。

2.9.2　详细步骤

(1) 参考 car.py 文件中的源代码。首先导入两个软件包：

from sklearn import preprocessingfrom sklearn.ensemble import RandomForestClassifier

(2) 加载数据集：

input_file = 'path/to/dataset/car.data.txt'# 读取数据X = []count = 0with open(input_file, 'r') as f:    for line in f.readlines():        data = line[:-1].split(',')        X.append(data)X = np.array(X)

每一行都包含由逗号分隔的单词列表。因此，我们解析输入文件，对每一行进行分割，然后将该列表附加到主数据。我们忽略每一行最后一个字符，因为那是一个换行符。由于 Python 程序包只能处理数值数据，所以需要把这些属性转换成程序包可以理解的形式。

(3) 在上一章中，我们介绍过标记编码。下面可以用这个技术把字符串转换成数值：

# 将字符串转化为数值label_encoder = []X_encoded = np.empty(X.shape)for i,item in enumerate(X[0]):    label_encoder.append(preprocessing.LabelEncoder())    X_encoded[:, i] = label_encoder[-1].fit_transform(X[:, i])X = X_encoded[:, :-1].astype(int)y = X_encoded[:, -1].astype(int)

由于每个属性可以取有限数量的数值，所以可以用标记编码器将它们转换成数字。我们需要为不同的属性使用不同的标记编码器，例如，lug_boot属性可以取3个不同的值，需要建立一个懂得给这3个属性编码的标记编码器。每一行的最后一个值是类，将它赋值给变量y。

(4) 接下来训练分类器：

# 建立随机森林分类器params = {'n_estimators': 200, 'max_depth': 8, 'random_state': 7}classifier = RandomForestClassifier(**params)classifier.fit(X, y)

你可以改变n_estimators和max_depth参数的值，观察它们如何改变分类器的准确性。我们将用一个标准化的方法处理参数选择问题。

(5) 下面进行交叉验证：

# 交叉验证from sklearn import cross_validationaccuracy = cross_validation.cross_val_score(classifier,        X, y, scoring='accuracy', cv=3)print "Accuracy of the classifier: " + str(round(100*accuracy. mean(), 2)) + "%"

一旦训练好分类器，我们就需要知道它是如何执行的。我们用三折交叉验证（three-fold cross-validation，把数据分3组，轮换着用其中两组数据验证分类器）来计算分类器的准确性。

(6) 建立分类器的主要目的就是要用它对孤立的和未知的数据进行分类。下面用分类器对一个单一数据点进行分类：

# 对单一数据示例进行编码测试input_data = ['vhigh', 'vhigh', '2', '2', 'small', 'low']input_data_encoded = [-1] * len(input_data)for i,item in enumerate(input_data):    input_data_encoded[i] = int(label_encoder[i].transform(input_data[i]))input_data_encoded = np.array(input_data_encoded)

第一步是把数据转换成数值类型。需要使用之前训练分类器时使用的标记编码器，因为我们需要保持数据编码规则的前后一致。如果输入数据点里出现了未知数据，标记编码器就会出现异常，因为它不知道如何对这些数据进行编码。例如，如果你把列表中的第一个值vhigh改成abcd，那么标记编码器就不知道如何编码了，因为它不知道怎么处理这个字符串。这就像是错误检查，看看输入数据点是否有效。

(7) 现在可以预测出数据点的输出类型了：

# 预测并打印特定数据点的输出output_class = classifier.predict(input_data_encoded)print "Output class:", label_encoder[-1].inverse_transform(output_class)[0]

我们用predict方法估计输出类型。如果输出被编码的输出标记，那么它对我们没有任何意义。因此，用inverse_transform方法对标记进行解码，将它转换成原来的形式，然后打印输出类。

第02章：创建分类器（下）

2.10　生成验证曲线

前面用随机森林建立了分类器，但是并不知道如何定义参数。本节来处理两个参数：n_estimators和max_depth参数。它们被称为超参数（hyperparameters），分类器的性能是由它们决定的。当改变超参数时，如果可以看到分类器性能的变化情况，那就再好不过了。这就是验证曲线的作用。这些曲线可以帮助理解每个超参数对训练得分的影响。基本上，我们只对感兴趣的超参数进行调整，其他参数可以保持不变。下面将通过可视化图片演示超参数的变化对训练得分的影响。

详细步骤

(1) 打开上一节的 Python 文件，加入以下代码：

# 验证曲线from sklearn.learning_curve import validation_curveclassifier = RandomForestClassifier(max_depth=4, random_state=7)parameter_grid = np.linspace(25, 200, 8).astype(int)train_scores, validation_scores = validation_curve(classifier, X, y, "n_estimators", parameter_grid, cv=5)print "\n##### VALIDATION CURVES #####"print "\nParam: n_estimators\nTraining scores:\n", train_scoresprint "\nParam: n_estimators\nValidation scores:\n", validation_ scores

在这个示例中，我们通过固定max_depth参数的值来定义分类器。我们想观察评估器数量对训练得分的影响，于是用parameter_grid定义了搜索空间。评估器数量会在25~200之间每隔8个数迭代一次，获得模型的训练得分和验证得分。

(2) 运行代码，可以在命令行工具中看到如图2-11所示的结果。

图　2-11

(3) 把数据画成图形：

# 画出曲线图plt.figure()plt.plot(parameter_grid, 100*np.average(train_scores, axis=1), color='black')plt.title('Training curve')plt.xlabel('Number of estimators')plt.ylabel('Accuracy')plt.show()

(4) 得到的图形如图2-12所示。

图　2-12

(5) 用类似的方法对max_depth参数进行验证：

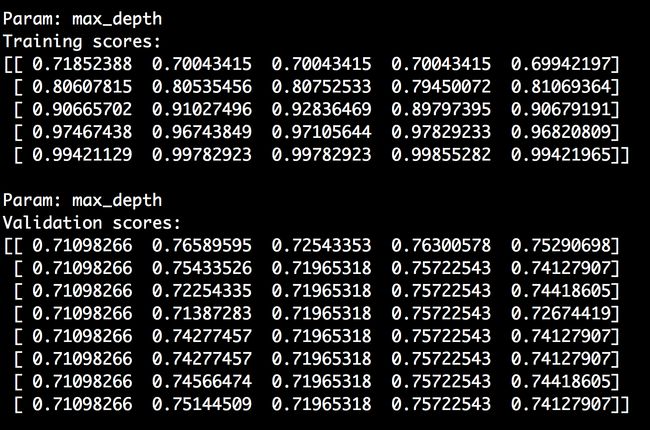
classifier = RandomForestClassifier(n_estimators=20, random_ state=7)parameter_grid = np.linspace(2, 10, 5).astype(int)train_scores, valid_scores = validation_curve(classifier, X, y, "max_depth",        parameter_grid, cv=5)print "\nParam: max_depth\nTraining scores:\n", train_scoresprint "\nParam: max_depth\nValidation scores:\n", validation_ scores

我们把n_estimators参数固定为20，看看max_depth参数变化对性能的影响。命令行工具的输出结果如图2-13所示。

(6) 把数据画成图形：

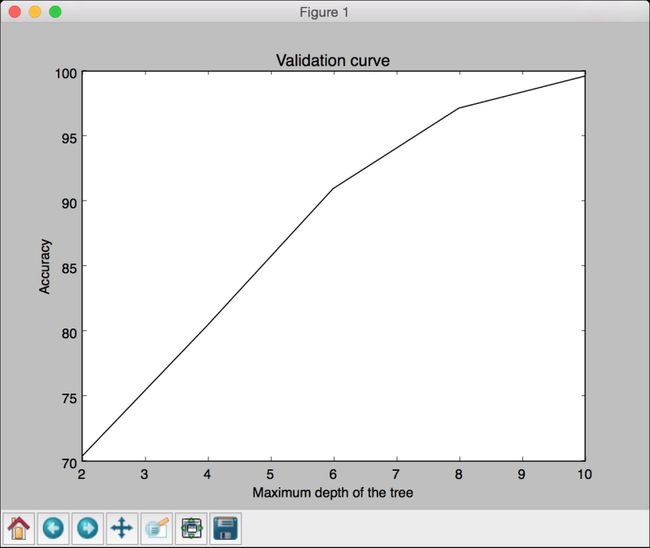
# 画出曲线图plt.figure()plt.plot(parameter_grid, 100*np.average(train_scores, axis=1), color='black')plt.title('Validation curve')plt.xlabel('Maximum depth of the tree')plt.ylabel('Accuracy')plt.show()

图　2-13

(7) 运行代码，可以看到如图2-14所示的图形。

图　2-14

2.11　生成学习曲线

学习曲线可以帮助我们理解训练数据集的大小对机器学习模型的影响。当遇到计算能力限制时，这一点非常有用。下面改变训练数据集的大小，把学习曲线画出来。

详细步骤

(1) 打开上一节的 Python 文件，加入以下代码：

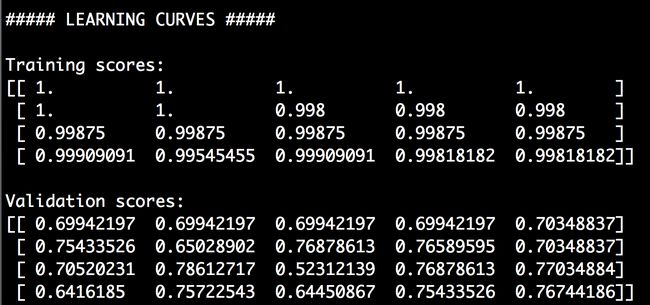
# 学习曲线from sklearn.learning_curve import learning_curveclassifier = RandomForestClassifier(random_state=7)parameter_grid = np.array([200, 500, 800, 1100])train_sizes, train_scores, validation_scores = learning_ curve(classifier,        X, y, train_sizes=parameter_grid, cv=5)print "\n##### LEARNING CURVES #####"print "\nTraining scores:\n", train_scoresprint "\nValidation scores:\n", validation_scores

我们想分别用200、500、800、1100的训练数据集的大小测试模型的性能指标。我们把learning_curve方法中的cv参数设置为5，就是用五折交叉验证。

(2) 运行代码，可以在命令行工具中看到如图2-15所示的结果。

图　2-15

(3) 把数据画成图形：

# 画出曲线图plt.figure()plt.plot(parameter_grid, 100*np.average(train_scores, axis=1), color='black')plt.title('Learning curve')plt.xlabel('Number of training samples')plt.ylabel('Accuracy')plt.show()

(4) 得到的图形如图2-16所示。

图　2-16

虽然训练数据集的规模越小，仿佛训练准确性越高，但是它们很容易导致过度拟合。如果选择较大规模的训练数据集，就会消耗更多的资源。因此，训练数据集的规模选择也是一个需要结合计算能力进行综合考虑的问题。

2.12　估算收入阶层

本节将根据14个属性建立分类器评估一个人的收入等级。可能的输出类型是“高于50K”和“低于或等于50K”。这个数据集稍微有点复杂，里面的每个数据点都是数字和字符串的混合体。数值数据是有价值的，在这种情况下，不能用标记编码器进行编码。需要设计一套既可以处理数值数据，也可以处理非数值数据的系统。我们将用美国人口普查收入数据集中的数据。

详细步骤

(1) 我们将用 income.py 文件作为参考，用朴素贝叶斯分类器解决问题。首先导入两个软件包：

from sklearn import preprocessingfrom sklearn.naive_bayes import GaussianNB

(2) 加载数据集：

input_file = 'path/to/adult.data.txt'# 读取数据X = []y = []count_lessthan50k = 0count_morethan50k = 0num_images_threshold = 10000

(3) 我们将使用数据集中的20 000个数据点——每种类型10 000个，保证初始类型没有偏差。在模型训练时，如果你的大部分数据点都属于一个类型，那么分类器就会倾向于这个类型。因此，最好使用每个类型数据点数量相等的数据进行训练：

with open(input_file, 'r') as f:    for line in f.readlines():        if '?' in line:            continue        data = line[:-1].split(', ')        if data[-1] == '<=50K' and count_lessthan50k < num_images_threshold:            X.append(data)            count_lessthan50k = count_lessthan50k + 1        elif data[-1] == '>50K' and count_morethan50k < num_images_threshold:            X.append(data)            count_morethan50k = count_morethan50k + 1        if count_lessthan50k >= num_images_threshold and count_morethan50k >= num_images_threshold:            breakX = np.array(X)

同样地，这也是一个带逗号分隔符的文件。我们还是像之前那样处理，把数据加载到变量X。

(4) 我们需要把字符串属性转换为数值数据，同时需要保留原有的数值数据：

# 将字符串转换为数值数据label_encoder = []X_encoded = np.empty(X.shape)for i,item in enumerate(X[0]):    if item.isdigit():        X_encoded[:, i] = X[:, i]    else:        label_encoder.append(preprocessing.LabelEncoder())        X_encoded[:, i] = label_encoder[-1].fit_transform(X[:, i])X = X_encoded[:, :-1].astype(int)y = X_encoded[:, -1].astype(int)

isdigit()函数帮助我们判断一个属性是不是数值数据。我们把字符串数据转换为数值数据，然后把所有的标记编码器保存在一个列表中，便于在后面处理未知数据时使用。

(5) 训练分类器：

# 建立分类器classifier_gaussiannb = GaussianNB()classifier_gaussiannb.fit(X, y)

(6) 把数据分割成训练数据集和测试数据集，方便后面获取性能指标：

# 交叉验证from sklearn import cross_validationX_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.25, random_state=5)classifier_gaussiannb = GaussianNB()classifier_gaussiannb.fit(X_train, y_train)y_test_pred = classifier_gaussiannb.predict(X_test)

(7) 提取性能指标：

# 计算分类器的F1得分f1 = cross_validation.cross_val_score(classifier_gaussiannb,        X, y, scoring='f1_weighted', cv=5)print "F1 score: " + str(round(100*f1.mean(), 2)) + "%"

(8) 接下来看看如何为单一数据点分类。我们需要把数据点转换成分类器可以理解的形式：

# 对单一数据示例进行编码测试input_data = ['39', 'State-gov', '77516', 'Bachelors', '13', 'Never-married', 'Adm-clerical', 'Not-in-family', 'White', 'Male', '2174', '0', '40', 'United-States']count = 0input_data_encoded = [-1] * len(input_data)for i,item in enumerate(input_data):    if item.isdigit():        input_data_encoded[i] = int(input_data[i])    else:        input_data_encoded[i] = int(label_encoder[count].transform(input_data[i]))        count = count + 1input_data_encoded = np.array(input_data_encoded)

(9) 这样就可以进行分类了：

# 预测并打印特定数据点的输出结果output_class = classifier_gaussiannb.predict(input_data_encoded)print label_encoder[-1].inverse_transform(output_class)[0]

和之前的分类案例一样，我们用predict方法获取输出类型，然后用inverse_transform对标记进行解码，将它转换成原来的形式，然后在命令行工具中打印出来。

第03章：预测建模（上）

第03章：预测建模（下）

第04章：无监督学习——聚类（上）

第04章：无监督学习——聚类（中）

第04章：无监督学习——聚类（下）

第05章：构建推荐引擎（上）

第05章：构建推荐引擎（中）

第05章：构建推荐引擎（下）

第06章：分析文本数据（上）

第06章：分析文本数据（中）

第06章：分析文本数据（下）

第07章：语音识别（上）

第07章：语音识别（下）

第08章：解剖时间序列和时序数据（上）

第08章：解剖时间序列和时序数据（下）

第09章：图像内容分析（上）

第09章：图像内容分析（下）

第10章：人脸识别（上）

第10章：人脸识别（中）

第10章：人脸识别（下）

第11章：深度神经网络（上）

第11章：深度神经网络（中）

第11章：深度神经网络（下）

第12章：可视化数据（上）

第12章：可视化数据（下）

阅读全文: http://gitbook.cn/gitchat/column/5a152e2f75462408e0db01f0