改进单纯形法的MATLAB实现

Simplex Algorithm

由George Dantzig发明的单纯形法（simplex
algorithm）在数学优化领域中常用于线性规划问题的数值求解。原单纯形法不是很经济的算法。1953年美国数学家G.B.丹齐克为了改进单纯形法每次迭代中积累起来的进位误差，提出改进单纯形法。其基本步骤和单纯形法大致相同，主要区别是在逐次迭代中不再以高斯消去法为基础，而是由旧基阵的逆去直接计算新基阵的逆，再由此确定检验数。这样做可以减少迭代中的累积误差，提高计算精度，同时也减少了在计算机上的存储量。
[1] “改进单纯形法_百度百科,” Baidu.com, 2018. [Online]. Available: https://baike.baidu.com/item/%E6%94%B9%E8%BF%9B%E5%8D%95%E7%BA%AF%E5%BD%A2%E6%B3%95/558282?fr=aladdin. [Accessed: 28-Mar-2020].

由高中学习的线性规划知识，我们知道线性规划问题的最优解在约束条件所形成的的凸多边形的顶点上取到。
而单纯形法的几何本质可以理解为沿凸多边形的边缘逐个尝试不同的顶点，直道找到最优解。

改进单纯形法？

改进在哪里？

原单纯形法都在上一轮迭代的基础上进行再迭代，在计算机内部由于浮点数的二进制近似表示，会在多次迭代后产生一定的累积误差，而改进单纯形法巧妙的利用了分块矩阵的性质避开了这个大坑。Let’s see how

下面我们列出单纯形法的标准形式和分块后的形式

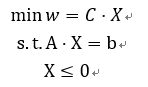
分块后的形式:

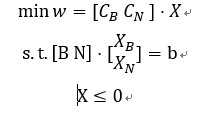
迭代后形式

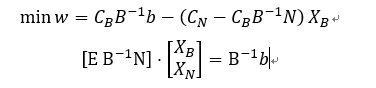
每次迭代，问题的描述形式都不变，只有基变量发生改变，而这些改变，都基于初始单纯形表，原数据没有被覆盖，故避开了累积误差的产生

下面简述了运算的过程，由于敲公式过于麻烦，假设大家都了解传统单纯形法的运算步骤（不清楚请参考百度）

1. 通过传统单纯形法的方法确定新的基变量与非基变量
2. 将基变量对应的系数矩阵变化为单位阵
3. 通过检验数确定是否达到最优解并决定是否继续迭代

下列代码展示一道例题的求解，前7行变量的值可以修改为其他数值：

例题原题

B = eye(2);
XB = [6 7]';
CB = zeros(1,2);
N = [2 3 3 2 2;3 5 4 2 4];
XN = [1:5]';
CN = [5 8 7 4 6];
b=[20 30]';

while(1)
    sigma = CN - CB*pinv(B)*N;
    [t in] = find(sigma==max(sigma)&sigma>0);  ##寻找入基变量
    
    if(isempty(in)) break;   ##判断是否有入基变量，若没有，则说明达到最优解
    end
    temp = pinv(B)*N(:,in);                                                  
    temp(find(temp<0)) = 0.000001;    #将小于零的如基变量的系数换成一个极小的数
    [out t] = find(pinv(B)*b./temp==min(pinv(B)*b./temp)) ;   #除以负值的数现为除以一个极小的数，所以不会被min选中
    t = XB(out);
    XB(out) = XN(in);
    XN(in) = t;   #更新基变量与非基变量
    t = B(:,out);
    B(:,out) = N(:,in);
    N(:,in) = t;  #更新基变量与非基变量的系数矩阵
    t=CB(out);
    CB(out)=CN(in);
    CN(in)=t;  #更新基变量与非基变量的价值系数
end

z = CB*pinv(B)*b

欢迎大佬批评指正