OpenGL.Shader:7-学习光照-法线向量
OpenGL.Shader:7-学习光照-法线向量
光照在OpenGL当中占据很重要的一部分。光照的仿真已经成为计算机领域的一个主要研究课题,我们可以看到这个领域的影响,这不仅仅反映在逐步提升的游戏视觉上,而且还反映在电影、电脑成像(CGI)等领域。
通常根据类型,可以把不同的光源分为下面几组:
环境光(Ambient light)
环境光看上去来自四面八方,场景中的一切被照亮的程度都一样。这近似于我们从大的、平等的光源获取的光照,比如天空,环境光也能用于虚构在光线到达我们的眼睛之前从许多物体弹开的效果,透过环境光阴影从来不会被漆成黑色。
方向光(Directional light)
方向光看上似乎来自一个方向,光源好像处于极其元的地方。这与我们从太阳或月亮获取的光照相似。
点光(Point light)
点光看上去是从附近某处投射的光亮,而且光的密度随着距离而减少。这适用于表示近处的光源,其把它们的光投射到四面八方,像一个灯泡或者蜡烛一样。
聚光(Spot light)
聚光与点光类似,只是加了一个限制,只能向一个特定的方向投射。这就像我们从手电筒或者聚光灯所获得的光照类型。
也可以根据把光线在物体表面发射的方式分为两类:
漫反射(Diffuse reflection)
漫反射是指光线平等地向所有方向蔓延,适用于表示没有抛光表面的材质,比如地毯或外面的混领土墙。这些类似的表面似乎有很多不用的观察点一样。
镜面反射(Specular reflection)
镜面反射在某个特定的方向上发射更加强烈,适用于被抛光的或者闪亮的材质,比如光滑的金属或者刚刚打过蜡的汽车。2
在OpenGL当中不会直接模拟这些光源,作为替代,大多数游戏和应用程序都会使事情简化,在较高的层次上近似于光线的工作方式,而不是直接模拟它。这就要介绍另外一个重要概念——法线向量。
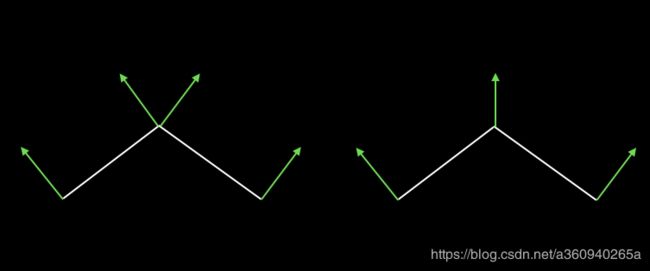
想象一下:一个平面如果刚好面朝光线,那自然是最亮的。当然还有些材质的平面可以反射光线,反射光线的强度和你观察的角度相关,不过这些本文都不会介绍。我们用法线向量来表示平面朝向,在具体实现中,每个点都会有一个法线向量。所谓法线向量就是垂直于平面的一个三维向量,如下图所示。
图中展示了两种法线向量的表示方法,左边是每个多边形的每个点有一个法线向量,右边是每个点有一个法线向量,共享点的法线向量是这个点在所有平面上的法线向量之和。法线向量应该总是被规范化成单位向量。本文的例子中使用的是左边的方式。
这里我们基于一直用的正方体为准,在原有的正方体(位置,纹理)数据增加法线向量。
class CubeIlluminate {
public:
struct V3N3T2 {
float x, y, z; //位置坐标
float nx, ny, nz; //法向量
float u,v; //纹理坐标
};
public:
GLuint mCubeSurfaceTexId;
V3N3T2 _data[36];
void init(const CELL::float3 &halfSize, GLuint tex)
{
V3N3 verts[] =
{
{+halfSize.x, -halfSize.y, +halfSize.z, 0.0f, -1.0f, 0.0f, 0.0f,0.0f},
{-halfSize.x, -halfSize.y, +halfSize.z, 0.0f, -1.0f, 0.0f, 1.0f,0.0f},
{-halfSize.x, -halfSize.y, -halfSize.z, 0.0f, -1.0f, 0.0f, 1.0f,1.0f},
{-halfSize.x, -halfSize.y, +halfSize.z, 0.0f, 0.0f, +1.0f, 0.0f,0.0f},
{+halfSize.x, -halfSize.y, +halfSize.z, 0.0f, 0.0f, +1.0f, 1.0f,1.0f},
{+halfSize.x, +halfSize.y, +halfSize.z, 0.0f, 0.0f, +1.0f, 0.0f,1.0f},
{+halfSize.x, +halfSize.y, -halfSize.z, +1.0f, 0.0f, 0.0f, 1.0f,0.0f},
{+halfSize.x, +halfSize.y, +halfSize.z, +1.0f, 0.0f, 0.0f, 1.0f,1.0f},
{+halfSize.x, -halfSize.y, +halfSize.z, +1.0f, 0.0f, 0.0f, 0.0f,1.0f},
{-halfSize.x, +halfSize.y, +halfSize.z, 0.0f, +1.0f, 0.0f, 1.0f,0.0f},
{+halfSize.x, +halfSize.y, +halfSize.z, 0.0f, +1.0f, 0.0f, 0.0f,1.0f},
{+halfSize.x, +halfSize.y, -halfSize.z, 0.0f, +1.0f, 0.0f, 0.0f,0.0f},
{-halfSize.x, +halfSize.y, +halfSize.z, -1.0f, 0.0f, 0.0f, 0.0f,1.0f},
{-halfSize.x, -halfSize.y, -halfSize.z, -1.0f, 0.0f, 0.0f, 0.0f,0.0f},
{-halfSize.x, -halfSize.y, +halfSize.z, -1.0f, 0.0f, 0.0f, 1.0f,0.0f},
{-halfSize.x, +halfSize.y, +halfSize.z, 0.0f, 0.0f, +1.0f, 0.0f,1.0f},
{-halfSize.x, -halfSize.y, +halfSize.z, 0.0f, 0.0f, +1.0f, 1.0f,0.0f},
{+halfSize.x, +halfSize.y, +halfSize.z, 0.0f, 0.0f, +1.0f, 1.0f,1.0f},
{+halfSize.x, -halfSize.y, -halfSize.z, 0.0f, -1.0f, 0.0f, 1.0f,1.0f},
{+halfSize.x, -halfSize.y, +halfSize.z, 0.0f, -1.0f, 0.0f, 0.0f,1.0f},
{-halfSize.x, -halfSize.y, -halfSize.z, 0.0f, -1.0f, 0.0f, 0.0f,0.0f},
{+halfSize.x, -halfSize.y, -halfSize.z, 0.0f, 0.0f, -1.0f, 1.0f,1.0f},
{-halfSize.x, -halfSize.y, -halfSize.z, 0.0f, 0.0f, -1.0f, 0.0f,0.0f},
{+halfSize.x, +halfSize.y, -halfSize.z, 0.0f, 0.0f, -1.0f, 1.0f,0.0f},
{+halfSize.x, -halfSize.y, -halfSize.z, +1.0f, 0.0f, 0.0f, 1.0f,0.0f},
{+halfSize.x, +halfSize.y, -halfSize.z, +1.0f, 0.0f, 0.0f, 1.0f,1.0f},
{+halfSize.x, -halfSize.y, +halfSize.z, +1.0f, 0.0f, 0.0f, 0.0f,1.0f},
{-halfSize.x, +halfSize.y, -halfSize.z, 0.0f, 0.0f, -1.0f, 1.0f,0.0f},
{+halfSize.x, +halfSize.y, -halfSize.z, 0.0f, 0.0f, -1.0f, 0.0f,1.0f},
{-halfSize.x, -halfSize.y, -halfSize.z, 0.0f, 0.0f, -1.0f, 0.0f,0.0f},
{-halfSize.x, +halfSize.y, -halfSize.z, -1.0f, 0.0f, 0.0f, 0.0f,0.0f},
{-halfSize.x, -halfSize.y, -halfSize.z, -1.0f, 0.0f, 0.0f, 1.0f,0.0f},
{-halfSize.x, +halfSize.y, +halfSize.z, -1.0f, 0.0f, 0.0f, 1.0f,1.0f},
{-halfSize.x, +halfSize.y, -halfSize.z, 0.0f, +1.0f, 0.0f, 0.0f,0.0f},
{-halfSize.x, +halfSize.y, +halfSize.z, 0.0f, +1.0f, 0.0f, 1.0f,1.0f},
{+halfSize.x, +halfSize.y, -halfSize.z, 0.0f, +1.0f, 0.0f, 0.0f,1.0f},
};
memcpy(_data, verts, sizeof(verts));
mCubeSurfaceTexId = tex;
}
// ... ...
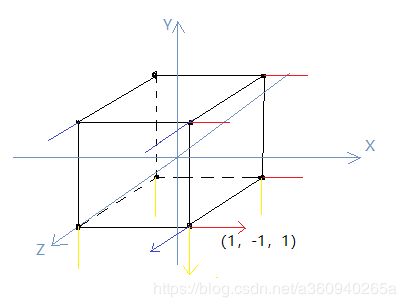
};鉴于数据量有点多,自定义结构体V3N3T2,代表一个点的数据量,然后每三组V3N3T2构成一个三角面,其他就不再啰嗦了。需要注意的是,法线向量只代表方向,不代表位置信息,所以法向向量尽量用归一化的数据。以上数据投射到笛卡尔空间如图所示
首先以左侧面的四点中的点(1,-1,1)为例,红色的就是对应左侧面的法向量(1,0,0)水平向右;
换成底面,同样是点(1,-1,1)为例,黄色的就是底面对应的法向量(0,-1,0)竖直向下;
再换成正面,同样是点(1,-1,1),蓝色的就是正面对应的法向量(0,0,1)垂直水平面朝外;
以上说明再一次认证了理论知识:1)法向量是代表方向,不是位置;2)法向量是归一化向量 即Math.sqrt(x*x + y*y + z*z)=1;3)法向量是基于面来确定的,方向是垂直于该平面,多个面的共点可以有多个法向量。
法向量基本介绍到这里,下面直奔着色器程序组。
class CubeIlluminateProgram : public ShaderProgram
{
public:
GLint _mvp;
GLint _lightDir;
GLint _lightColor;
GLint _lightDiffuse;
GLint _texture;
GLint _position;
GLint _normal;
GLint _uv;
public:
virtual void initialize()
{
const char* vs = "#version 320 es\n\
uniform mat4 _mvp;\n\
uniform vec3 _lightDir;\n\
uniform vec3 _lightColor;\n\
uniform vec3 _lightDiffuse;\n\
in vec3 _position;\n\
in vec3 _normal;\n\
in vec2 _uv;\n\
out vec2 _outUV;\n\
out vec4 _outComposeColor;\n\
void main()\n\
{\n\
_outUV = _uv; \n\
float lightStrength = max(dot(_normal, -_lightDir), 0.0); \n\
_outComposeColor = vec4(_lightColor * lightStrength + _lightDiffuse, 1);\n\
gl_Position = _mvp * vec4(_position,1.0);\n\
}";
const char* fs = "#version 320 es\n\
precision mediump float;\n\
in vec4 _outComposeColor;\n\
in vec2 _outUV;\n\
uniform sampler2D _texture;\n\
out vec4 _fragColor;\n\
void main()\n\
{\n\
vec4 color = texture(_texture,_outUV);\n\
_fragColor = color * _outComposeColor;\n\
}";
programId = ShaderHelper::buildProgram(vs, fs);
_mvp = glGetUniformLocation(programId, "_mvp");
_lightDir = glGetUniformLocation(programId, "_lightDir");
_lightColor = glGetUniformLocation(programId, "_lightColor");
_lightDiffuse = glGetUniformLocation(programId, "_lightDiffuse");
_position = glGetAttribLocation(programId, "_position");
_normal = glGetAttribLocation(programId, "_normal");
_uv = glGetAttribLocation(programId, "_uv");
_texture = glGetUniformLocation(programId, "_texture");
}
virtual void begin()
{
glEnableVertexAttribArray(_position);
glEnableVertexAttribArray(_normal);
glEnableVertexAttribArray(_uv);
glUseProgram(programId);
}
virtual void end()
{
glDisableVertexAttribArray(_position);
glDisableVertexAttribArray(_normal);
glDisableVertexAttribArray(_uv);
glUseProgram(0);
}
};先分析顶点着色器程序:
#version 320 es uniform mat4 _mvp; // 模型视图投影矩阵 uniform vec3 _lightDir; // 光源方向 只是一个方向 uniform vec3 _lightColor; // 环境光源颜色 uniform vec3 _lightDiffuse; // 漫反射 模拟材质补光用 in vec3 _position; // 顶点位置属性 in vec3 _normal; // 顶点法向量 in vec2 _uv; // 纹理坐标 out vec2 _outUV; // 输出片元着色器纹理坐标 out vec4 _outComposeColor; // 输出的混合光 void main() { _outUV = _uv; float lightStrength = max(dot(_normal, -_lightDir), 0.0); _outComposeColor = vec4(_lightColor * lightStrength + _lightDiffuse, 1); gl_Position = _mvp * vec4(_position,1.0); }
第二行代码 光照强度 = 法向量 * 反向归化后的光源向量 。从数学公式来说,光照强度就是法向量与反向归化后的光源向量的点积。什么是反向归化后的光源,看下图,so easy。
也有些网络教程直接把输入的法向量直接取反,从数学运算的角度来说是一致,但是这样不容易在理论上去理解,本人不建议这样的方式。知道有这么回事就可以了,能看懂别人的一些骚操作就行。
得到光照强度之后,第三行代码 vec4(_lightColor * lightStrength + _lightDiffuse, 1),光照强度*环境光色值,这时其实已经具备光照效果,加上漫反射_lightDiffuse是防止没有光照强度的地方会完全变黑,那如实际情况不相符。漫反射还有很多内容可以扩充,譬如根据纹理的材质进行漫反射的光强度计算,添加自己的色值等等。
version 320 es precision mediump float; in vec4 _outComposeColor; in vec2 _outUV; uniform sampler2D _texture; out vec4 _fragColor; void main() { vec4 color = texture(_texture,_outUV); _fragColor = color * _outComposeColor; }
之后来到片元着色器程序,着色器程序就比较简单了,根据纹理坐标提取纹理色值, 然后以纹理色值为基础乘以从顶点输出过来的混合光照色,大功告成。
最后结合着色器程序,补上CubeIlluminate的渲染方法。
void render(Camera3D& camera)
{
sprogram.begin();
CELL::matrix4 matModel(1);
CELL::matrix4 vp = camera.getProject() * camera.getView();
CELL::matrix4 mvp = (vp * matModel);
glUniformMatrix4fv(sprogram._mvp, 1, GL_FALSE, mvp.data());
glActiveTexture(GL_TEXTURE0);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D, mCubeSurfaceTexId);
glUniform1i(sprogram._texture, 0);
glUniform3f(sprogram._lightDiffuse, 0.1f, 0.1f, 0.1f); // 漫反射 环境光
glUniform3f(sprogram._lightColor, 1.0f, 1.0f, 1.0f); // 定向光源的颜色
glUniform3f(sprogram._lightDir, // 定向光源的方向 直接使用摄像头到观察点的方向
static_cast(camera._dir.x),
static_cast(camera._dir.y),
static_cast(camera._dir.z));
glVertexAttribPointer(static_cast(sprogram._position), 3, GL_FLOAT, GL_FALSE,
sizeof(CubeIlluminate::V3N3), &_data[0].x);
glVertexAttribPointer(static_cast(sprogram._normal), 3, GL_FLOAT, GL_FALSE,
sizeof(CubeIlluminate::V3N3), &_data[0].nx);
glVertexAttribPointer(static_cast(sprogram._uv), 2, GL_FLOAT, GL_FALSE,
sizeof(CubeIlluminate::V3N3), &_data[0].u);
glDrawArrays(GL_TRIANGLES, 0, 36);
sprogram.end();
}
Demo工程链接 https://github.com/MrZhaozhirong/NativeCppApp ->LightRenderer.cpp CubeIlluminate.hpp CubeIlluminateProgram.hpp
最后一起来最简单的光照法线 效果: