机器学习-线性回归总结
最近学习了线性回归的模型,也是机器学习中最基础的一种模型。在此,总结一下线性回归的模型介绍、梯度下降以及正规方程。
回归问题
线性回归,顾名思义,属于回归问题。既然是回归问题,那必然属于监督学习。
在这里简单再介绍一下什么是回归问题,回归用于预测输入变量和输出变量之间的关系,特别是当输入变量的值发生变化时,输出变量的值随之发生的变化。回归模型正是表示从输入变量到输出变量之间映射的函数,回归问题的学习等价于函数拟合:选择一条函数曲线使其很好地拟合已知数据且很好地预测未知数据。
线性回归模型
线性回归的定义是:目标值预期是输入变量的线性组合。线性模型形式简单、易于建模,但却蕴含着机器学习中一些重要的基本思想。线性回归,是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。
简单来说,就是选择一条线性函数来很好的拟合已知数据并预测未知数据。
模型描述
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
举一个简单的例子,比如房价和房间大小的关系。根据我们的生活经验,我们知道房价和房间大小存在着正相关的关系,即房价通常随着房间的大小增大而增大。
假设我们现在手里有一些数据,这些数据就是相应的房间大小与其对应的房价。如图:
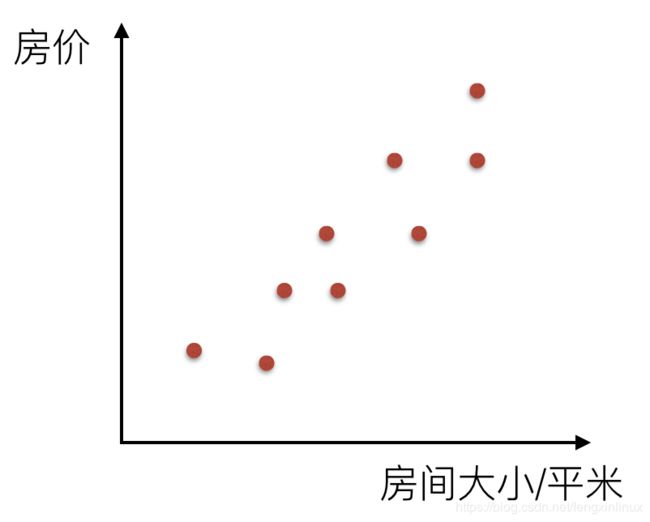
因此,我们可以根据已有的数据集,找到一条最合适的直线,来预测其他房间大小对应的价格。如图:
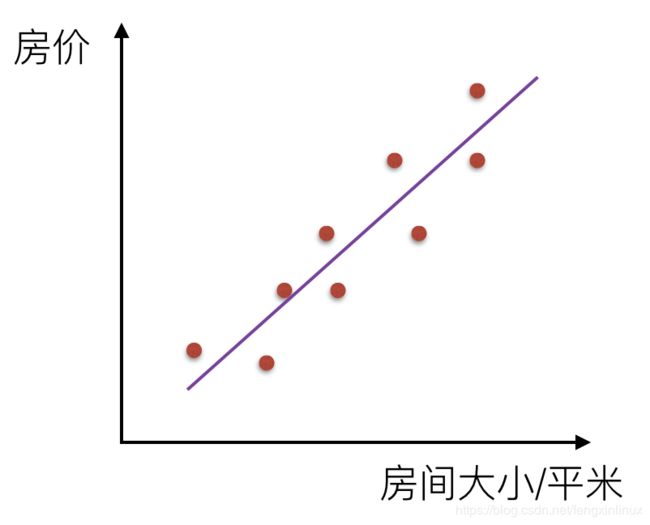
这个例子就是一个一元线性回归的问题,因为一元线性回归可以看成是多元线性回归的一个简单情况。所以,我们直接引出多元线性回归模型的定义。
多元线性回归模型定义:
h θ ( x i ) = θ 0 + θ 1 x 1 + θ 2 x 2 + … + θ n x n \begin{aligned}h_{\theta }\left( x^i\right) =\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+\ldots +\theta _{n}x_{n}\end{aligned} hθ(xi)=θ0+θ1x1+θ2x2+…+θnxn
我们默认x0总是等于1。
为了方便表示,我们把假设函数可以写成向量的形式。
h θ ( x i ) = θ T X . \begin{aligned}h_{\theta }\left( x^i\right) =\theta ^{T}X\\ .\end{aligned} hθ(xi)=θTX.
其中,
θ = [ θ 0 , θ 1 , … , θ n ] T \theta =\left[ \theta _{0},\theta _{1},\ldots ,\theta _{n}\right] ^{T} θ=[θ0,θ1,…,θn]T
X = [ 1 , X 1 , X 2 , . . . , x n ] T X=\left[ 1,X_{1},X_{2},...,x_{n}\right] ^{T} X=[1,X1,X2,...,xn]T
假设有训练集:

那么为了方便我们写成矩阵的形式

X θ = h θ ( x i ) X\theta =h_{\theta }\left( x^{i}\right) Xθ=hθ(xi)
损失函数
现在,我们要根据已知数据集,在假设空间中,选出最合适的线性回归模型。这时,就要引出损失函数。即找出使损失函数最小的向量 θ \theta θ。
线性回归中,损失函数用均方误差表示,即最小二乘法。
何为最小二乘法,其实很简单。我们有很多的给定点,这时候我们需要找出一条线去拟合它,那么我先假设这个线的方程,然后把数据点代入假设的方程得到观测值,求使得实际值与观测值相减的平方和最小的参数。
因此损失代价函数为:
J ( θ ) = 1 2 m ∑ i = 0 m ( h θ ( x i ) − y i ) 2 = 1 2 m ( X θ − y ) T ( X θ − y ) J(\theta)=\frac1{2m}\sum_{i=0}^m(h_\theta(x^i)-y^i)^2=\frac1{2m}\left( X\theta -y\right) ^{T}\left( X\theta -y\right) J(θ)=2m1i=0∑m(hθ(xi)−yi)2=2m1(Xθ−y)T(Xθ−y)
其中, ⋅ y = [ y 0 , y 1 , … , y n ] T \begin{aligned}\cdot \\ y=\left[ y_{0},y_{1},\ldots ,y_{n}\right] ^{T}\end{aligned} ⋅y=[y0,y1,…,yn]T
算法
现在,我们的目标就成了求解向量 θ \theta θ使得 J ( θ ) J(\theta) J(θ)最小。
有两种方法,一种是梯度下降法,是搜索算法,先给 θ 赋个初值,然后再根据使 J(θ) 更小的原则对 θ 进行修改,直到最小 θ 收敛,J(θ) 达到最小,也就是不断尝试;另外一种是正规方程法,要使 J(θ) 最小,就对 θ 求导,使导数等于 0,求得 θ。
下面我们将详细介绍这两种算法。
梯度下降
梯度下降算法在机器学习中是很普遍的算法,不仅可以用于线性回归问题,还可以应用到其他很多的机器学习的问题中。
梯度下降算法是一种求局部最优解的方法,对于F(x),在a点的梯度是F(x)增长最快的方向,那么它的相反方向则是该点下降最快的方向。
原理:将函数比作一座山,我们站在某个山坡上,往四周看,从哪个方向向下走一小步,能够下降的最快;
注意:当变量之间大小相差很大时,应该先将他们做处理,对特征值进行相应的缩放,使得他们的值尽量在同一个范围,这样会收敛的更快些,我们称之为特征值缩放。
1)首先对θ赋值,这个值可以是随机的,也可以让θ是一个全零的向量。
2)改变θ的值,使得J(θ)按梯度下降的方向进行减少。
在这个过程中,我们需要先对J(θ)对 θ j \theta_j θj求偏导,

因此,最后的梯度下降算法公式如下图,

其中α 是步长,也称学习率,步子小了收敛慢,步子大了容易跳过收敛值,然后在收敛值附近震荡。所以,使用梯度下降的过程中,需要我们不断尝试不同的α ,从而找到最合适的α 。
将对J(θ)对 θ j \theta_j θj求偏导的结果代入,可化简为:

也就是,

线性回归使用梯度下降算法最优化问题只有一个全局最优,没有其它局部最优。这是因为 J(θ) 是凸二次函数。所以这里的梯度下降会一直收敛到全局最小。
需要注意的一些问题
梯度下降算法是通过每次迭代后,使得当前的向量 θ \theta θ代入J(θ)损失函数后,使得其值逐渐减少,直到最后收敛。
在实际的操作过程中,我们可能会遇到J(θ)经过迭代后,其值不但没有减少反而增大的反常情况,那么这种情况通常是因为我们选取的学习率α太大,我们需要减小α。当然,我们又不能使α太小,从而使得收敛需要的迭代的次数太大。
正规方程法
梯度下降算法需要经过多次迭代,最后达到收敛。而正规方程法,提供了一种求解最优 θ \theta θ的解析解法。因此,运用正规方法,我们不需要迭代,而直接一次性求出 θ \theta θ的最优解。
其实,求解最优解 θ \theta θ,我们只需要对J(θ)函数对每个 θ j \theta_j θj(j=0,1,…,n)求偏导,求出每个 θ j \theta_j θj使得偏导等于0。这些解组合成对应的向量 θ \theta θ,就是最优解。

正规方程其实就是帮我们推导出了一个结果公式,省去我们对每个j求偏导再求解,我们只需要使用这个公式,就能直接求出最后的最优化的值 θ \theta θ。
即, θ = ( X T X ) − 1 X T y \theta =\left( X^{T}X\right) ^{-1}X^{T}y θ=(XTX)−1XTy。
其中,X和y我们上边介绍过,再写一遍吧。

⋅ y = [ y 0 , y 1 , … , y n ] T \begin{aligned}\cdot \\ y=\left[ y_{0},y_{1},\ldots ,y_{n}\right] ^{T}\end{aligned} ⋅y=[y0,y1,…,yn]T
因此,我们使用正规方程,只需要把对应的矩阵X,向量y代入式子 θ = ( X T X ) − 1 X T y \theta =\left( X^{T}X\right) ^{-1}X^{T}y θ=(XTX)−1XTy,进行矩阵的相关运算,就能直接得到最优 θ \theta θ。
PS:细心的可能会发现,正规方程用到了矩阵的逆求解,那如果 ( X T X ) − 1 \left( X^{T}X\right) ^{-1} (XTX)−1不存在怎么办?
其实,大部分的时候,解决线性回归问题求出来的 X T X X^{T}X XTX是可逆的,如果真的出现了不可逆的情况,如何还想继续使用正规方程求解的化,我们可以使用伪逆矩阵,即求出一个逆矩阵,使得其乘它的原矩阵的结果近似等于单位矩阵E。在Octave中,使用pinv函数求逆时,若矩阵不可逆,输出的结果就是伪逆矩阵。
可能还会有小伙伴对正规方程的公式是如何得到的感兴趣,那我们就在这简单证明一下吧:
证明:
J ( θ ) = 1 2 m ∑ i = 0 m ( h θ ( x i ) − y i ) 2 = 1 2 m ( X θ − y ) T ( X θ − y ) = 1 2 m ( θ T X T − y T ) ( X θ − y ) = 1 2 m ( θ T X T X θ − θ T X T y − y T x θ + y T y ) = 1 2 m ( θ T X T X θ − 2 θ T X T y + y T y ) J(\theta)=\frac1{2m}\sum_{i=0}^m(h_\theta(x^i)-y^i)^2 \\ =\frac {1}{2m}\left( X\theta -y\right) ^{T}\left( X\theta -y\right) \\ =\dfrac {1}{2m}\left( \theta ^{T}X^{T}-y^{T}\right) \left( X\theta -y\right) \\ =\dfrac {1}{2m}\left( \theta ^{T}X^{T}X\theta -\theta ^{T}X^{T}y-y^{T}x\theta +y^{T}y\right) \\ =\dfrac {1}{2m}\left( \theta ^{T}X^{T}X\theta -2\theta ^{T}X^{T}y+y^{T}y\right) J(θ)=2m1i=0∑m(hθ(xi)−yi)2=2m1(Xθ−y)T(Xθ−y)=2m1(θTXT−yT)(Xθ−y)=2m1(θTXTXθ−θTXTy−yTxθ+yTy)=2m1(θTXTXθ−2θTXTy+yTy)
因此,对 J ( θ ) J(\theta) J(θ)求偏导,令偏导数等于0可得:
∂ J ( θ ) ∂ θ = 0 \dfrac {\partial J\left( \theta \right) }{\partial \theta }=0 ∂θ∂J(θ)=0
运用对向量求导的知识(不清楚的可以查一下向量和矩阵求导),可得:
∂ J ( θ ) ∂ θ = 0 ⇒ 1 2 m ( 2 X T X θ − 2 X T y ) = 0 ⇒ X T X θ = X T y ⇒ θ = ( X T X ) − 1 X T y \begin{aligned}\dfrac {\partial J\left( \theta \right) }{\partial \theta }=0\\ \Rightarrow \dfrac {1}{2m}\left( 2X^{T}X\theta -2X^{T}y\right) =0\\ \Rightarrow X^{T}X\theta =X^{T}y\\ \Rightarrow \theta =\left( X^{T}X\right) ^{-1}X^{T}y\end{aligned} ∂θ∂J(θ)=0⇒2m1(2XTXθ−2XTy)=0⇒XTXθ=XTy⇒θ=(XTX)−1XTy
即,得证。
梯度下降法和正规方程对比
- 梯度下降算法有时需要我们对特征值进行适当的缩放,正规方程不需要特征缩放
- 梯度下降算法需要我们自己选择适当的学习率α ,且需要多次的迭代运算。而正规方程并不需要。
- 相比梯度下降,当n不是很大时,正规方程得到结果更快一些,一般线性回归问题更偏向运用正规方程,但是梯度下降法在机器学习中适用范围更大。
- 当n很大时,这时矩阵运算的代价就变的很大,所以正规方程求解也会变的很慢,所以梯度下降更适合特征变量很多的情况,一般n小于10000时,选择正规方程是没问题的。